Капиллярные мосты

Капиллярный мостик — это минимизированная поверхность жидкости или мембраны, созданная между двумя твердыми телами произвольной формы. Между двумя жидкостями также могут образовываться капиллярные мостики. Плато определяло последовательность форм капилляров. известный как (1) нодоид с «шеей», (2) катеноид , (3) ундулоид с «шеей», (4) цилиндр , (5) ундулоид с «бедром» (6) сфера и (7) нодоид с «бедром» ' . Наличие капиллярных перемычек в зависимости от их формы может привести к притяжению или отталкиванию между твердыми телами. Простейшими их случаями являются осесимметричные. Мы выделили три важных класса перемычек в зависимости от формы поверхности соединяемых тел:

• две плоские поверхности (рис.1)

рис.1 Вогнутый капиллярный мостик между двумя плоскостями (схематическое изображение)

• плоская поверхность и сферическая частица (рис. 2)

рис.2 Вогнутая капиллярная перемычка между частицами и плоской поверхностью (схематическое изображение)

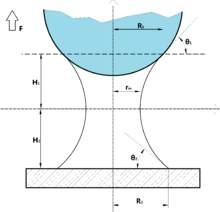
• две сферические частицы (частицы вообще могут быть не одинакового размера, рис. 3)

рис.3 Вогнутый капиллярный мостик между двумя частицами (схематическое изображение)

На капиллярные мосты и их свойства также могут влиять гравитация Земли и свойства соединяемых поверхностей. Мостиковое вещество может быть жидкостью или газом. Вмещающая граница называется границей раздела ( капиллярной поверхностью ). Интерфейс характеризуется особым поверхностным натяжением .

История

Капиллярные мосты изучаются уже более 200 лет. Впервые вопрос был поставлен Жозефом Луи Лагранжем в 1760 году, а дальнейшее распространение интереса вызвал французский астроном и математик Ш. Делоне . Делоне открыл совершенно новый класс осесимметричных поверхностей постоянной средней кривизны . Формулировка и доказательство его теоремы имели долгую историю. Все началось с Эйлера предложение новой фигуры, называемой катеноидом . (Намного позже Кенмоцу решил сложные нелинейные уравнения, описывающие этот класс поверхностей. Однако его решение не имеет большого практического значения, поскольку не имеет геометрической интерпретации.) Ж. Плато показал существование таких фигур с заданными границами. Задача была названа в его честь проблемой Плато .
Многие учёные внесли свой вклад в решение проблемы. Один из них — Томас Янг. Пьер Симон Лаплас ввел понятие капиллярного натяжения. Лаплас даже сформулировал широко известное ныне условие механического равновесия между двумя жидкостями, разделенными капиллярной поверхностью P _γ =Δ P, т.е. капиллярное давление между двумя фазами уравновешивается соседней разностью давлений.
Общий обзор поведения капиллярных мостиков в поле силы тяжести завершен Мышкисом и Бабским.
В прошлом веке много усилий было приложено к изучению поверхностных сил, вызывающих капиллярные эффекты мостиков. Установлено, что эти силы возникают в результате межмолекулярных сил и становятся существенными в тонких жидкостных зазорах (<10 нм) между двумя поверхностями.
Неустойчивость капиллярных мостиков впервые обсуждалась Рэлеем . Он продемонстрировал, что струя жидкости или капиллярная цилиндрическая поверхность становятся неустойчивыми, когда отношение ее длины H к радиусу R становится больше 2π. В условиях малых синусоидальных возмущений с длиной волны больше его периметра площадь поверхности цилиндра становится больше, чем у невозмущенного цилиндра того же объема и, следовательно, он становится неустойчивым. Позже Хоув сформулировал вариационные требования к устойчивости осесимметричных капиллярных поверхностей (неограниченных) в отсутствие силы тяжести и при возмущениях, ограниченных постоянным объемом. Он впервые решил уравнение Юнга-Лапласа для равновесных форм и показал, что условие Лежандра для второго варианта всегда выполняется. Следовательно, устойчивость определяется отсутствием отрицательного собственного значения линеаризованного уравнения Юнга-Лапласа. Такой подход определения устойчивости по второму варианту в настоящее время широко используется. Методы возмущений стали очень успешными, несмотря на то, что нелинейный характер капиллярного взаимодействия может ограничивать их применение. Другие методы теперь включают прямое моделирование. На тот момент большинство методов определения устойчивости требовали расчета равновесия как основы возмущений. Появилась новая идея о том, что устойчивость можно вывести из состояний равновесия. Это предложение было дополнительно доказано Питтсом. для осесимметричного постоянного объема. В последующие годы Фогель расширил теорию. Он исследовал случай осесимметричных капиллярных мостиков с постоянными объемами, где изменения устойчивости соответствуют точкам поворота. Недавнее развитие теории бифуркаций доказало, что обмен устойчивостью между точками поворота и точками ветвления является общим явлением.

Приложения и явления

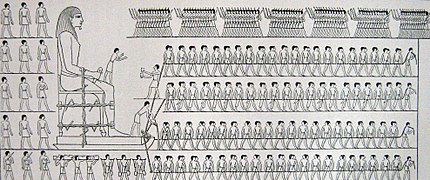
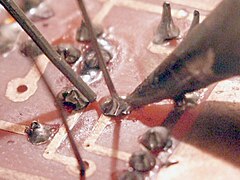
Недавние исследования показали, что древние египтяне использовали свойства песка для создания капиллярных мостиков, используя воду. Таким образом, они уменьшали поверхностное трение и были способны перемещать статуи и тяжелые камни пирамид. Некоторые виды современного искусства, такие как искусство песка , также тесно связаны со способностью воды связывать частицы. В атомно-силовой микроскопии , когда кто-то работает в среде с повышенной влажностью, на его исследования может повлиять появление наноразмерных капиллярных мостиков. Эти перемычки появляются при приближении рабочего кончика к исследуемому образцу. Капиллярные мостики также играют важную роль в процессе пайки .

• 
  Схема из гробницы Джехутиххотепа , изображающая транспортировку колоссальной статуи.
• 
  АСМ
• 
  Пайка
• 
  Белогубая древесная лягушка

Капиллярные мостики также широко распространены в живой природе. Насекомые, мухи, кузнечики и древесные лягушки способны прикрепляться к вертикальным шероховатым поверхностям из-за их способности впрыскивать смачивающую жидкость в область контакта подушки с подложкой. Таким образом создается дальнодействующее притягивающее взаимодействие за счет образования капиллярных мостиков. Многие медицинские проблемы, связанные с респираторными заболеваниями и здоровьем суставов тела, зависят от крошечных капиллярных мостиков. Жидкие мостики в настоящее время широко используются при выращивании клеточных культур из-за необходимости имитировать работу живых тканей в научных исследованиях.

Общие уравнения

Общее решение профиля капилляра известно исходя из учета ондулоидной или нодоидной кривизны.
Предположим, что используется следующая цилиндрическая система координат: z показывает ось вращения; r представляет собой радиальную координату, а φ — это угол между нормалью и положительной осью z . Узлоид имеет вертикальные касательные в точках r = r ₁ и r = r ₂ и горизонтальную касательную в точках r = r ₃ . Когда φ — это угол между нормалью к интерфейсу и положительной z осью , тогда φ равен 90°, 0°, -90° для нодоида.

Уравнение Юнга-Лапласа можно записать в форме, удобной для интегрирования с точки зрения осевой симметрии:

$\Delta P=\gamma \left({\frac {1}{R_{1}}}+{\frac {1}{R_{2}}}\right)=\gamma {\frac {d\left(r\sin \phi \right)}{rdr}}={\rm {constant}},$ ( 1 )

где R ₁ , R ₂ — радиусы кривизны, а γ — межфазное поверхностное натяжение.
Интегрирование уравнения называется первым интегралом и дает:

$\sin \phi ={\frac {\left(r^{2}-r_{1}r_{2}\right)}{r\left(r_{1}-r_{2}\right)}}$ ( 2 )

С:

${\frac {dz}{dr}}=-\tan \phi =-{\frac {\sin \phi }{\sqrt {\left(1-\sin ^{2}\phi \right)}}}$ ( 3 )

Находится:

${\frac {dz}{dr}}={\frac {r_{1}r_{2}-r^{2}}{\sqrt {\left(r^{2}-r_{1}^{2}\right)\left(r_{2}^{2}-r^{2}\right)}}}$ ( 4 )

После интегрирования полученное уравнение называется вторым интегралом :

$z=\pm \left[r_{1}F\left(r,\phi \right)-r_{2}E\left(r,\phi \right)\right]+{\frac {\sqrt {\left(1-{\frac {r_{0}^{2}}{r^{2}}}\right)\left({\frac {r_{1}^{2}}{r^{2}}}-1\right)}}{r}}$ ( 5 )

где: F и E — эллиптические интегралы первого и второго рода, ${\textstyle k^{2}={\frac {r_{1}^{2}-r_{2}^{2}}{r_{1}^{2}}}}$ и φ связана с r согласно

$\sin ^{2}\phi ={\frac {r^{2}-r_{2}^{2}}{k^{2}r^{2}}}$.

Ундулоид имеет только вертикальные касательные при r = r ₁ и r = r ₂ , где φ = + 90. Совершенно аналогично:

${\frac {dz}{dr}}={\frac {r_{1}r_{2}+r^{2}}{\sqrt {\left(r^{2}-r_{1}^{2}\right)\left(r_{2}^{2}-r^{2}\right)}}}$ ( 6 )

Второй интеграл для ундулоида получается:

$z=\pm \left[r_{1}F\left(r,\phi \right)+r_{2}E\left(r,\phi \right)\right]+{\frac {\sqrt {\left(1-{\frac {r_{0}^{2}}{r^{2}}}\right)\left({\frac {r_{1}^{2}}{r^{2}}}-1\right)}}{r}}$ ( 7 )

где связь между параметрами k и φ определяется так же, как указано выше. В предельном случае r ₁ =0 как нодоид, так и ондулоид состоят из серии сфер. Когда р ₁ = р ₂ . Последний и очень интересный предельный случай — катеноид . Уравнение Лапласа сводится к:

${\frac {d\left(r\sin r\right)}{rdr}}=0$ ( 8 )

Интегрирование можно представить в очень удобной форме, в цилиндрической системе координат, называемой цепным уравнением :

${\frac {r}{r_{1}}}=\cosh \left({\frac {z}{r_{1}}}\right)$ ( 9 )

Рис. 4. Область существования катеноида (1) высота масштабируется по радиусу R, (2) высота масштабируется по кубическому корню из объема (действительно только для капиллярных мостиков C=0)

Уравнение (9) важно, поскольку оно в некотором упрощении показывает прозрачно все вопросы, связанные с капиллярными мостиками. На рисунке в безразмерных координатах показан максимум, различающий две ветви. Один из них энергетически выгоден и возможен в статике, а другой (пунктирная линия) энергетически не выгоден. Максимум важен, поскольку при растяжении квазиравновесного пути капиллярного мостика при достижении максимума происходит его разрыв. В процессе динамического растяжения/сжатия могут образовываться катеноиды энергетически невыгодных размеров. Нулевое капиллярное давление C =0 естественно для классического катеноида (капиллярной мыльной поверхности, натянутой между двумя коаксиальными кольцами). Когда типичный капиллярный мост переходит в катеноидное состояние C = 0, несмотря на то, что свойства его поверхности такие же, как у классического катеноида, его более уместно представить в масштабе кубического корня из его объема, а не радиуса R .

Решение второго интеграла различно в случаях сплюснутых капиллярных мостиков (узловидных и ундулоидных):

$z=\pm \left[r_{2}F\left(r,\phi \right)-\left(C-1\right)r_{2}E\left(r,\phi \right)\right]$ ( 10 )

где: F и E — снова эллиптические интегралы первого и второго рода, ${\textstyle k^{2}={\frac {r_{2}^{2}-r_{1}^{2}}{r_{2}^{2}}}}$ и φ связана с r согласно: ${\textstyle \sin ^{2}\phi ={\frac {r_{2}^{2}-r^{2}}{k^{2}r_{2}^{2}}}}$.
Важно отметить, что все описанные кривые получены прокаткой конического участка без скольжения по оси z . Ундулоид описывается фокусом катящегося эллипса, который может вырождаться в линию, сферу или параболу, приводя к соответствующим предельным случаям. Точно так же нодоид описывается фокусом катящейся гиперболы.

Хорошо систематизированная сводка форм капиллярных мостиков представлена ​​в таблице 11.1 книги Кральчевского и Нагаямы.

Статика между двумя плоскими поверхностями

Механическое равновесие включает в себя баланс давления на границе раздела жидкость/газ и внешнюю силу на пластинах Δ P , уравновешивающую капиллярное притяжение или отталкивание. $P_{\gamma }$, то есть $\Delta P=P_{\gamma }$. При пренебрежении гравитационными эффектами и другими внешними полями баланс давлений равен Δ P = P _i - P _e (Индексы «i» и «e» обозначают соответственно внутреннее и внешнее давления). В случае осевой симметрии уравнение для капиллярного давления принимает вид:

$P_{\gamma }=\gamma {\frac {d(r\sin {\phi })}{rdr}}$ ( 11 )

где γ – межфазное натяжение жидкость/газ; r — радиальная координата, а φ — угол между осью симметрии и нормалью к образующей интерфейса.
Первый интеграл легко получить относительно безразмерного капиллярного давления на контакте с поверхностью:

$C={\frac {X\sin {\theta }-1}{X^{2}-1}}$ ( 12 )

где ${\textstyle C=P_{\gamma }{\frac {r_{m}}{2\gamma }}}$, безразмерный радиус контакта равен ${\textstyle X={\frac {R}{r_{m}}}}$ — θ угол контакта. Соотношение показывает, что капиллярное давление может быть положительным или отрицательным. Форма капиллярных мостиков определяется уравнением:

${\frac {dy}{dx}}=\pm {\frac {C\left(x^{2}-1\right)+1}{\sqrt {x^{2}-\left[C\left(x^{2}-1\right)+1\right]^{2}}}}$ ( 13 )

где уравнение получается после замены ${\textstyle \sin \phi ={\frac {dy}{dx}}\cos \phi }$ производится в уравнении ( 11 ) и масштабирование ${\textstyle x={\frac {r}{r_{m}}}}$ вводится.

Тонкий жидкий мостик

В отличие от случаев увеличения высоты капиллярных перемычек, что обуславливает разнообразие форм профиля, уплощение (утончение) к нулевой толщине носит гораздо более универсальный характер. Универсальность появляется, когда H << R (рис. 1). Уравнение (11) можно записать:

$C\left(X=1-\Delta \right)\approx -{\frac {1-\sin \theta }{2\Delta }}+{\frac {1+\sin \theta }{4}}$ ( 14 )

Образующая сходится к уравнению:

${\frac {dy}{dx}}=\pm {\frac {1+2C\left(x-1\right)}{\sqrt {1-\left[2C\left(x-1\right)+1\right]^{2}}}}$ ( 15 )

После интегрирования уравнение дает:

рис.5. Тонкий жидкий мостик

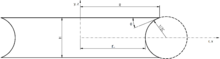
$y^{2}+\left(x+1\pm {\frac {1}{2C}}\right)^{2}=\left({\frac {1}{2C}}\right)^{2}$ ( 16 )

Безразмерные круговые радиусы 1/2С совпадают с радиусами кривизны капиллярного мостика. Положительный знак «+» представляет образующую профиля вогнутой перемычки, а отрицательный знак «-» — сплющенный. Для выпуклых капиллярных мостиков круговая образующая сохраняется до тех пор, пока при растяжении не будет достигнута граница области определения. Ближе к началу кинетики самоинициируемого разрушения профиль моста последовательно превращается в эллипс, параболу и, возможно, в гиперболу.

Домен определения

Наблюдения, представленные на рис. 5 указывают на то, что можно определить область существования капиллярных мостиков. Поэтому при растяжении жидкого мостика он может прекратить свое существование не только из-за возникновения неустойчивостей, но и из-за достижения некоторых точек, в которых форма больше не может существовать. Оценка области определения требует манипулирования интегрированными уравнениями для высоты капиллярного мостика и его объема. Оба они интегрируемы, но интегралы несобственные. Применяемый метод включает расщепление интеграла на две части: сингулярную, но интегрируемую аналитически, и регулярную, но интегрируемую только численным способом.
После интегрирования для высоты капиллярного мостика получим

$H^{*}\equiv \left({\frac {H}{\sqrt[{3}]{V}}}\right)={\frac {1}{X}}\left({\frac {R}{\sqrt[{3}]{V}}}\right)\left\{{\frac {\pi }{4C}}-\alpha \left(X,C\right)-\int \limits _{1}^{X}{\sqrt {\frac {\zeta -C\left(X^{2}-1\right)+1}{\zeta +C\left(X^{2}-1\right)+1}}}d\zeta \right\}$ ( 17 )

Аналогичным образом для радиуса контакта R получается интегральное уравнение

$R^{*}\equiv \left({\frac {R}{\sqrt[{3}]{V}}}\right)={\frac {X}{\sqrt[{3}]{2\pi }}}\left\{\beta \left(C\right){\frac {\pi }{4C}}-{\frac {\sqrt {\left(1-2C\right)\left(X^{2}-1\right)}}{2C^{2}}}-\beta \left(C\right)\alpha \left(X,C\right)-\int \limits _{1}^{X}\zeta ^{2}{\sqrt {\frac {\zeta -C\left(X^{2}-1\right)+1}{\zeta +C\left(X^{2}-1\right)+1}}}d\zeta \right\}^{-{\frac {1}{3}}}$ ( 18 )

где $\beta \left(C\right)=\left[1-{\frac {\left(1-2C\right)}{2C^{2}}}\right]$ и $\alpha \left(C,X\right)={\frac {1}{2C}}\arcsin \left[\beta \left(C\right)-X^{2}{\frac {2C^{2}}{1-2C}}\right]$

Рис. 6. Изогоны, демонстрирующие статическую область капиллярных мостиков, красная кривая показывает катеноидное состояние C=0.

На рис. 6 показано количество устойчивых статических состояний жидкого капиллярного мостика, представленное двумя характерными параметрами: (i) безразмерной высотой, которая получается масштабированием высоты капиллярного мостика кубическим корнем из его объема (уравнение). ( 16 ) и (ii) его радиус, также масштабированный кубическим корнем из объема, уравнение. ( 17 ). Частично аналитические решения, полученные для этих двух параметров, представлены выше. Решения каким-то образом отличаются от широко распространенного подхода Плато [эллиптическими функциями, уравнение. ( 7 )], поскольку они предлагают удобный численный подход для интегрирования регулярных интегралов, в то время как нерегулярная часть уравнения интегрировалась аналитически. Эти решения в дальнейшем стали основой для прогнозирования квазиравновесного растяжения и разрушения капиллярных мостиков при углах смачивания менее 45°. ${\textstyle \left(0\leq \theta \leq {\frac {\pi }{4}}\right)}$. Практическая реализация позволяет идентифицировать не только конец области определения, но и точное поведение во время растяжения капиллярного мостика. потому что в координатах ${\textstyle {\frac {H}{r_{m}}}\sim \ln \left({\frac {R}{r_{m}}}\right)}$ растяжение образует наклонную линию, угол наклона которой пропорционален углу контакта.

Вогнутый капиллярный мостик

Случай вогнутого капиллярного мостика представлен изогонами для краевых углов ниже. ${\textstyle {\frac {\pi }{2}}}$ на рис. 6, ${\textstyle \left(0\leq \theta <{\frac {\pi }{2}}\right)}$. Изогоны имеют четко выраженный максимум. ${\textstyle {\frac {dH^{*}}{dR^{*}}}\equiv {\frac {dH}{dR}}=0}$. Этот максимум отмечен точкой для каждой изогоны. Он снова, подобно простому катеноиду, разделяет две ветви. Левая ветвь энергетически выгодна, а правая энергетически невыгодна.

Цилиндрический капиллярный мостик

Этот случай хорошо проанализирован Рэлеем. Обратите внимание, что область определения в его случае не имеет ограничений и стремится к бесконечности, рис. 6, ${\textstyle \left(\theta ={\frac {\pi }{2}}\right)}$. Однако обычно наблюдается разрыв цилиндрических капиллярных мостиков. Это происходит в результате хорошо изученной неустойчивости, известной теперь как неустойчивость Рэлея . Область определения изогоны 90° показана на рис. 6 пунктирной линией.

Выпуклый капиллярный мостик

Случай выпуклых капиллярных мостиков представлен на рис. 6, ${\textstyle \left({\frac {\pi }{2}}<\theta \leq \pi \right)}$ слева от области цилиндрического корпуса.

Устойчивость между двумя плоскими поверхностями

Равновесные формы и пределы устойчивости капиллярных жидких мостиков являются предметом многочисленных теоретических и экспериментальных исследований. Исследования в основном сосредоточены на изучении мостов между равными дисками в условиях гравитации. Хорошо известно, что для каждого значения числа Бонда , определяемого как ${\textstyle {\rm {Bo}}={\frac {\rho gR^{2}}{\gamma }}}$ (где: g — ускорение свободного падения Земли, γ — поверхностное натяжение и R — радиус контакта) диаграмму устойчивости можно представить в виде одной замкнутой кусочной кривой на плоскости гибкости/безразмерного объема. Гибкость определяется как ${\textstyle {\frac {H}{2R}}}$, а безразмерный объем представляет собой объем капиллярного мостика, разделенный на объем цилиндра той же высоты H и радиуса R : ${\textstyle {\frac {V}{\pi R^{2}H}}}$.

Если и гибкость, и объем жидкости достаточно малы, пределы устойчивости определяются отрывом формы жидкости от краев дисков (трехфазная линия контакта), линия АВ на рис. 7. Линия BC представляет собой минимум объема, соответствующий осесимметричному обрыву. В литературе он известен как стабильности объема минимальный предел . Кривая CA представляет собой еще один предел стабильности, характеризующий максимальный объем. Это верхняя граница области устойчивости. Также существует переходная область между минимальной и максимальной стабильностью объема. Он еще четко не определен и поэтому отмечен пунктирной линией на рис. 7.

См. также

• Число Этвеша
• Капиллярная конденсация