Гетеропереход

Гетеропереход — это граница раздела между двумя слоями или областями разнородных полупроводников . Эти полупроводниковые материалы имеют неравную ширину запрещенной зоны в отличие от гомоперехода . Часто бывает выгодно спроектировать электронные энергетические зоны во многих твердотельных устройствах, включая полупроводниковые лазеры, солнечные элементы и транзисторы. Комбинация нескольких гетеропереходов в устройстве называется гетероструктурой , хотя эти два термина обычно используются как синонимы. Требование, чтобы каждый материал был полупроводником с неравной шириной запрещенной зоны, является несколько неопределенным, особенно на малых масштабах длины, где электронные свойства зависят от пространственных свойств. Более современное определение гетероперехода — это интерфейс между любыми двумя твердотельными материалами, включая кристаллические и аморфные структуры металлических, изолирующих, проводников быстрых ионов и полупроводниковых материалов.

Производство и применение

Производство гетеропереходов обычно требует использования молекулярно-лучевой эпитаксии (МЛЭ). или технологии химического осаждения из паровой фазы (CVD) для точного контроля толщины осаждения и создания четко согласованной с решеткой резкой границы раздела. Недавней альтернативой, находящейся в стадии исследования, является механическая укладка слоистых материалов в гетероструктуры Ван-дер-Ваальса .

Несмотря на свою дороговизну, гетеропереходы нашли применение во множестве специализированных приложений, где их уникальные характеристики имеют решающее значение:

• Солнечные элементы . В некоторых конструкциях солнечных элементов гетеропереходы образуются на границе раздела кристаллической кремниевой подложки (запрещенная зона 1,1 эВ) и тонкой пленки аморфного кремния (запрещенная зона 1,7 эВ). Гетеропереход используется для разделения носителей заряда аналогично p-n-переходу . Гетеропереход с внутренней тонкослойной структурой солнечного элемента (HIT) был впервые разработан в 1983 году. и коммерциализируется Sanyo / Panasonic . Солнечные элементы HIT теперь являются рекордсменом среди самых эффективных однопереходных кремниевых солнечных элементов с эффективностью преобразования 26,7%.
• Лазеры использовать гетеропереходы в лазерах. : впервые было предложено в 1963 году, когда Герберт Кремер , выдающийся ученый в этой области, предположил, что инверсия населенности может быть значительно усилена гетероструктурами. Включив с прямой запрещенной зоной материал меньшего размера, такой как GaAs, между двумя слоями с более широкой запрещенной зоной, например AlAs , носители можно ограничить так, что генерация может происходить при комнатной температуре с низкими пороговыми токами. изготовления гетероструктур потребовалось много лет, Материаловедению чтобы догнать идеи Кремера, но теперь это отраслевой стандарт. Позже было обнаружено, что ширину запрещенной зоны можно контролировать, используя квантово -размерные эффекты в гетероструктурах с квантовыми ямами . Кроме того, гетероструктуры можно использовать в качестве волноводов для преломления границы раздела, что является еще одним важным преимуществом их использования в полупроводниковых лазерах. Полупроводниковые диодные лазеры, используемые в компакт-дисков и DVD проигрывателях , а также волоконно-оптических трансиверах, производятся с использованием чередующихся слоев различных III-V и II-VI полупроводников для формирования лазерных гетероструктур.
• Биполярные транзисторы . Когда гетеропереход используется в качестве перехода база-эмиттер биполярного транзистора , получается чрезвычайно высокий прямой коэффициент усиления и низкий обратный коэффициент усиления. Это приводит к очень хорошей работе на высоких частотах (значения от десятков до сотен ГГц) и низким токам утечки . Это устройство называется биполярным транзистором с гетеропереходом (ГБТ).
• Полевые транзисторы . Гетеропереходы используются в транзисторах с высокой подвижностью электронов (HEMT), которые могут работать на значительно более высоких частотах (более 500 ГГц). Правильный профиль легирования и выравнивание зон приводят к чрезвычайно высокой подвижности электронов за счет создания двумерного электронного газа в области, свободной от примесей , где может происходить очень незначительное рассеяние .

Выравнивание энергетических диапазонов

Три типа полупроводниковых гетеропереходов, организованных по принципу выравнивания зон.

Зонная диаграмма страдинговой щели, n - n полупроводниковый гетеропереход в равновесии.

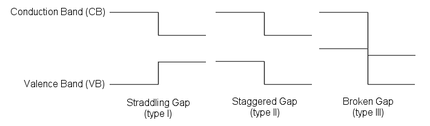
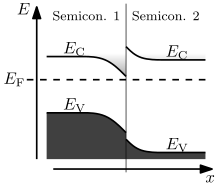
Поведение полупроводникового перехода решающим образом зависит от расположения энергетических зон на границе раздела. Полупроводниковые интерфейсы могут быть организованы в три типа гетеропереходов: смешанный зазор (тип I), шахматный зазор (тип II) или разрыв зазора (тип III), как показано на рисунке. Вдали от перехода изгиб зоны можно рассчитать на основе обычной процедуры решения уравнения Пуассона .

Существуют различные модели для прогнозирования выравнивания полос.

• Самая простая (и наименее точная) модель — это правило Андерсона , которое предсказывает выравнивание зон на основе свойств границ раздела вакуум-полупроводник (в частности, сродства вакуума к электрону ). Основным ограничением является пренебрежение химическими связями.
• Было предложено общее правило анионов , согласно которому, поскольку валентная зона связана с анионными состояниями, материалы с одинаковыми анионами должны иметь очень небольшие смещения валентной зоны. Однако это не объясняет данные, но связано с тенденцией того, что два материала с разными анионами имеют тенденцию иметь большее валентной зоны смещение , чем смещение зоны проводимости .
• Терсофф предложил модель щелевого состояния , основанную на более известных переходах металл-полупроводник , где смещение зоны проводимости определяется разницей в высоте барьера Шоттки . Эта модель включает дипольный слой на границе раздела между двумя полупроводниками, который возникает в результате туннелирования электронов из зоны проводимости одного материала в щель другого материала (аналогично состояниям щели, индуцированным металлом ). Эта модель хорошо согласуется с системами, в которых оба материала имеют близко согласованную решетку. такие как GaAs / AlGaAs .
• Правило 60:40 представляет собой эвристику для конкретного случая соединений полупроводника GaAs и полупроводникового сплава Al _x Ga _{1− x} As. Поскольку x на стороне Al _x Ga _{1− x} As изменяется от 0 до 1, отношение $\Delta E_{C}/\Delta E_{V}$ имеет тенденцию поддерживать значение 60/40. Для сравнения: правило Андерсона предсказывает $\Delta E_{C}/\Delta E_{V}=0.73/0.27$ для перехода GaAs/AlAs ( x =1).

Типичным методом измерения смещений полос является их расчет на основе измерения экситонов энергий в спектрах люминесценции .

Эффективное несоответствие масс

Когда гетеропереход образован двумя разными полупроводниками , квантовая яма может быть изготовлена ​​из-за различия в зонной структуре . Для расчета статических уровней энергии внутри полученной квантовой ямы становится важным понимание изменения или несоответствия эффективной массы в гетеропереходе. Квантовую яму, определенную в гетеропереходе, можно рассматривать как потенциал конечной ямы шириной $l_{w}$. Кроме того, в 1966 г. Конли и др. и БенДэниел и Дюк сообщил о граничном условии для огибающей функции в квантовой яме, известном как граничное условие Бен-Дэниела-Дьюка. По их мнению, огибающая функция в искусственно созданной квантовой яме должна удовлетворять граничному условию, которое гласит, что $\psi (z)$ и ${\frac {1}{m^{*}}}{\partial \over {\partial z}}\psi (z)\,$ оба непрерывны в областях интерфейса.

показывать

Математические детали проработаны на примере квантовой ямы .

Using the Schrödinger equation for a finite well with width of $l_{w}$and center at 0, the equation for the achieved quantum well can be written as:

$-{\frac {\hbar ^{2}}{2m_{b}^{*}}}{\frac {\mathrm {d} ^{2}\psi (z)}{\mathrm {d} z^{2}}}+V\psi (z)=E\psi (z)\quad \quad {\text{ for }}z<-{\frac {l_{w}}{2}}\quad \quad (1)$

$\quad \quad -{\frac {\hbar ^{2}}{2m_{w}^{*}}}{\frac {\mathrm {d} ^{2}\psi (z)}{\mathrm {d} z^{2}}}=E\psi (z)\quad \quad {\text{ for }}-{\frac {l_{w}}{2}}<z<+{\frac {l_{w}}{2}}\quad \quad (2)$

$-{\frac {\hbar ^{2}}{2m_{b}^{*}}}{\frac {\mathrm {d} ^{2}\psi (z)}{\mathrm {d} z^{2}}}+V\psi (z)=E\psi (z)\quad {\text{ for }}z>+{\frac {l_{w}}{2}}\quad \quad (3)$

Solution for above equations are well-known, only with different(modified) k and $\kappa$

$k={\frac {\sqrt {2m_{w}E}}{\hbar }}\quad \quad \kappa ={\frac {\sqrt {2m_{b}(V-E)}}{\hbar }}\quad \quad (4)$.

At the z = $+{\frac {l_{w}}{2}}$ even-parity solution can be gained from

$A\cos({\frac {kl_{w}}{2}})=B\exp(-{\frac {\kappa l_{w}}{2}})\quad \quad (5)$.

By taking derivative of (5) and multiplying both sides by ${\frac {1}{m^{*}}}$

$-{\frac {kA}{m_{w}^{*}}}\sin({\frac {kl_{w}}{2}})=-{\frac {\kappa B}{m_{b}^{*}}}\exp(-{\frac {\kappa l_{w}}{2}})\quad \quad (6)$.

Dividing (6) by (5), even-parity solution function can be obtained,

$f(E)=-{\frac {k}{m_{w}^{*}}}\tan({\frac {kl_{w}}{2}})-{\frac {\kappa }{m_{b}^{*}}}=0\quad \quad (7)$.

Similarly, for odd-parity solution,

$f(E)=-{\frac {k}{m_{w}^{*}}}\cot({\frac {kl_{w}}{2}})+{\frac {\kappa }{m_{b}^{*}}}=0\quad \quad (8)$.

For numerical solution, taking derivatives of (7) and (8) gives

even parity:

${\frac {df}{dE}}={\frac {1}{m_{w}^{*}}}{\frac {dk}{dE}}\tan({\frac {kl_{w}}{2}})+{\frac {k}{m_{w}^{*}}}\sec ^{2}({\frac {kl_{w}}{2}})\times {\frac {l_{w}}{2}}{\frac {dk}{dE}}-{\frac {1}{m_{b}^{*}}}{\frac {d\kappa }{dE}}\quad \quad (9-1)$

odd parity:

${\frac {df}{dE}}={\frac {1}{m_{w}^{*}}}{\frac {dk}{dE}}\cot({\frac {kl_{w}}{2}})-{\frac {k}{m_{w}^{*}}}\csc ^{2}({\frac {kl_{w}}{2}})\times {\frac {l_{w}}{2}}{\frac {dk}{dE}}+{\frac {1}{m_{b}^{*}}}{\frac {d\kappa }{dE}}\quad \quad (9-2)$

where ${\frac {dk}{dE}}={\frac {\sqrt {2m_{w}^{*}}}{2{\sqrt {E}}\hbar }}\quad \quad \quad {\frac {d\kappa }{dE}}=-{\frac {\sqrt {2m_{b}^{*}}}{2{\sqrt {V-E}}\hbar }}$.

The difference in effective mass between materials results in a larger difference in ground state energies.

Наномасштабные гетеропереходы

Изображение наноразмерного гетероперехода между оксидом железа (Fe ₃ O ₄ — сфера) и сульфидом кадмия (CdS — стержень), полученное с помощью ПЭМ . Это смещенное соединение с шахматным зазором (тип II) было синтезировано Хантером МакДэниелом и доктором Мунсуб Шим в Университете Иллинойса в Урбана-Шампейн в 2007 году.

В квантовых точках энергии зон зависят от размера кристалла из-за квантово-размерных эффектов . Это позволяет реализовать технологию смещения зон в наноразмерных гетероструктурах. Это возможно использовать те же материалы, но изменить тип соединения, скажем, с шахматного (тип I) на шахматное (тип II), изменив размер или толщину задействованных кристаллов. Наиболее распространенной наноразмерной гетероструктурной системой является ZnS на CdSe (CdSe@ZnS), которая имеет смещенный межзональный зазор (тип I). В этой системе гораздо большая запрещенная зона ZnS пассивирует поверхность флуоресцентного тем самым увеличивая квантовую эффективность люминесценции ядра CdSe , . Дополнительным преимуществом является повышенная термическая стабильность за счет более прочных связей в оболочке ZnS, о чем свидетельствует большая запрещенная зона. Поскольку CdSe и ZnS растут в кристаллической фазе цинковой обманки и имеют близкое согласование по решетке, предпочтительным является рост ядра-оболочки. В других системах или при других условиях выращивания можно вырастить анизотропные структуры, подобные той, что видна на изображении справа.

Движущей силой переноса заряда между зонами проводимости в этих структурах является смещение зоны проводимости. Уменьшив размер нанокристаллов CdSe, выращенных на TiO ₂ , Robel et al. обнаружили, что электроны переходят быстрее из зоны проводимости CdSe в TiO ₂ . В CdSe квантово-размерный эффект гораздо более выражен в зоне проводимости из-за меньшей эффективной массы, чем в валентной зоне, и это характерно для большинства полупроводников. Следовательно, спроектировать смещение зоны проводимости обычно намного проще с помощью наноразмерных гетеропереходов. Для наноразмерных гетеропереходов с шахматным смещением (тип II) может происходить фотоиндуцированное разделение зарядов , поскольку там самое низкое энергетическое состояние для дырок может находиться на одной стороне перехода, тогда как самая низкая энергия для электронов находится на противоположной стороне. Было предложено что анизотропные наноразмерные гетеропереходы с шахматной щелью (тип II) могут быть использованы для фотокатализа , в частности для расщепления воды с помощью солнечной энергии.

См. также

• Гомопереход , p–n-переход — переход двух типов одного и того же полупроводника.
• Переход металл-полупроводник — переход металла с полупроводником.

Дальнейшее чтение

• Ублюдок, Жеральд (1991). Волновая механика в приложении к полупроводниковым гетероструктурам . Уайли-Интерсайенс . ISBN  978-0-470-21708-5 .
• Фейхт, Д. Лион; Милнс, АГ (1970). Гетеропереходы и переходы металл–полупроводник . Нью-Йорк и Лондон : Академическая пресса . , ISBN   0-12-498050-3 . Несколько устаревший справочник по приложениям, но всегда является хорошим введением в основные принципы гетеропереходных устройств.
• Р. Цу; Ф. Зипман (1990). «Новые идеи в физике резонансного туннелирования». Поверхностная наука . 228 (1–3): 418. Бибкод : 1990SurSc.228..418T . дои : 10.1016/0039-6028(90)90341-5 .
• Курхекар, Анил Судхакар (2018). «Термический отжиг улучшает электрические свойства диода с гетеропереходом». Международная конференция по исследованиям и образованию в области возобновляемых источников энергии (Rere-2018) . Материалы конференции AIP. Том. 1992. с. 040027. Бибкод : 2018AIPC.1992d0027K . дои : 10.1063/1.5047992 .