мощность переменного тока

Эта статья о мощности в системах переменного тока. Информацию о питании переменным током от сети см. в разделе « Сетевое электричество» .

На этой длинной выдержке показано мигание городских огней без ламп накаливания. Переменный характер сетевого напряжения можно определить по штриховым следам движущихся огней.

В электрической цепи мгновенная мощность — это скорость потока энергии в заданной точке цепи во времени. В цепях переменного тока элементы накопления энергии, такие как катушки индуктивности и конденсаторы, могут приводить к периодическому изменению направления потока энергии. Его единица СИ — ватт .

Часть мгновенной мощности, которая, усредненная за полный цикл сигнала переменного тока , приводит к чистой передаче энергии в одном направлении, известна как мгновенная активная мощность, а ее среднее по времени известно как активная мощность или реальная мощность . Часть мгновенной мощности, которая не приводит к чистой передаче энергии, а вместо этого колеблется между источником и нагрузкой в ​​каждом цикле из-за накопленной энергии, известна как мгновенная реактивная мощность, а ее амплитуда представляет собой абсолютное значение реактивной мощности .

Активная, реактивная, полная и комплексная мощность в синусоидальном установившемся режиме.

В простой цепи переменного тока (AC), состоящей из источника и линейной , не зависящей от времени нагрузки, ток и напряжение имеют синусоидальную форму с одинаковой частотой. Если нагрузка чисто резистивная , обе величины одновременно меняют свою полярность. Следовательно, мгновенная мощность, определяемая произведением напряжения и тока, всегда положительна, так что направление потока энергии не меняется на противоположное и всегда направлено к резистору. В этом случае передается только активная мощность.

Если нагрузка чисто реактивная , то напряжение и ток сдвинуты по фазе на 90 градусов. В течение двух четвертей каждого цикла произведение напряжения и тока положительно, но в течение двух других четвертей произведение отрицательно, что указывает на то, что в среднем в нагрузку поступает ровно столько энергии, сколько уходит обратно. В течение каждого полупериода нет чистого потока энергии. В этом случае течет только реактивная мощность: нет чистой передачи энергии в нагрузку; однако электрическая мощность течет по проводам и возвращается, проходя в обратном направлении по тем же проводам. Ток, необходимый для этого потока реактивной мощности, рассеивает энергию на сопротивлении линии, даже если устройство идеальной нагрузки само по себе не потребляет энергии. Практические нагрузки обладают сопротивлением, а также индуктивностью или емкостью, поэтому к нормальным нагрузкам передаются как активная, так и реактивная мощности.

Полная мощность представляет собой произведение среднеквадратичных значений напряжения и тока. Полная мощность учитывается при проектировании и эксплуатации энергосистем, поскольку хотя ток, связанный с реактивной мощностью, не работает на нагрузке, он все равно должен поступать от источника питания. Проводники, трансформаторы и генераторы должны быть рассчитаны на передачу полного тока, а не только тока, совершающего полезную работу. Недостаточная реактивная мощность может снизить уровень напряжения в электрической сети и, при определенных условиях эксплуатации, привести к разрушению сети ( отключение электроэнергии ). Другим последствием является то, что сложение полной мощности двух нагрузок не даст точной общей мощности, если только они не имеют одинаковую разность фаз между током и напряжением (одинаковый коэффициент мощности ).

Обычно конденсаторы рассматриваются так, как будто они генерируют реактивную мощность, а катушки индуктивности рассматриваются так, как будто они ее потребляют. Если конденсатор и катушка индуктивности расположены параллельно, то токи, протекающие через конденсатор и катушку индуктивности, имеют тенденцию компенсироваться, а не суммироваться. Это фундаментальный механизм управления коэффициентом мощности при передаче электроэнергии; конденсаторы (или катушки индуктивности) вставляются в цепь для частичной компенсации реактивной мощности, «потребляемой» («генерируемой») нагрузкой. Чисто емкостные схемы передают реактивную мощность, при этом форма волны тока опережает форму волны напряжения на 90 градусов, тогда как чисто индуктивные цепи поглощают реактивную мощность, при этом форма волны тока отстает от формы волны напряжения на 90 градусов. Результатом этого является то, что емкостные и индуктивные элементы цепи имеют тенденцию нейтрализовать друг друга.

Треугольник власти
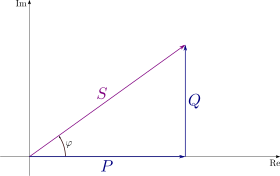
Комплексная мощность представляет собой векторную сумму активной и реактивной мощности. Полная мощность – это величина комплексной мощности.
  Активная мощность , П
  Реактивная мощность , Ом
  Комплексная мощность , С
  Полная мощность , |S|
  Фаза напряжения относительно тока , $\varphi$

Инженеры используют следующие термины для описания потока энергии в системе (и назначают каждому из них разные единицы, чтобы различать их):

• Активная мощность , P , или реальная мощность : ватт (Вт);
• Реактивная мощность , Q : реактивная вольт-амперная мощность (вар);
• Комплексная мощность , С : вольт-ампер (ВА);
• Полная мощность , | S |: величина комплексной мощности S : вольт-ампер (ВА);
• Фаза напряжения относительно тока , φ : угол разницы (в градусах) между током и напряжением; $\varphi =\arg(V)-\arg(I)$. Текущее напряжение задержки ( квадранта I), текущее опережающее напряжение (вектор квадранта IV). вектор

Все они обозначены на соседней диаграмме (называемой степенным треугольником).

На диаграмме P — активная мощность, Q — реактивная мощность (в данном случае положительная), S — комплексная мощность, а длина S — полная мощность. Реактивная мощность не совершает никакой работы, поэтому ее изображают в виде мнимой оси векторной диаграммы. Активная мощность действительно работает, поэтому это настоящая ось.

Единицей мощности является ватт (обозначение: Вт). Полная мощность часто выражается в вольт-амперах (ВА), поскольку она является произведением среднеквадратичного напряжения и среднеквадратичного тока . Единицей реактивной мощности является вар, что означает реактивный вольт-ампер . Поскольку реактивная мощность не передает чистую энергию нагрузке, ее иногда называют «бесваттной» мощностью. Однако он выполняет важную функцию в электрических сетях , и его отсутствие было названо важным фактором отключения электроэнергии на северо-востоке страны в 2003 году . Понимание взаимосвязи между этими тремя величинами лежит в основе понимания энергетики. Математическая связь между ними может быть представлена ​​векторами или выражена с помощью чисел комплексных S = P + j Q (где j — мнимая единица измерения ).

Мгновенная мощность в системах переменного тока при отставании тока от напряжения на 50 градусов.

Расчеты и уравнения в синусоидальном установившемся режиме

Формула комплексной мощности (единицы измерения: ВА) в векторной форме:

$S=VI^{*}=|S|\angle \varphi$,

где V обозначает напряжение в векторной форме с амплитудой как RMS , а I обозначает ток в векторной форме с амплитудой как RMS. Также по соглашению комплексное сопряжение I , которое обозначается используется $I^{*}$ (или ${\overline {I}}$), а не я сама. Это сделано потому, что в противном случае использование продукта VI для определения S приведет к величине, которая зависит от исходного угла, выбранного для V или I, но определение S как VI * приводит к величине, которая не зависит от исходного угла и позволяет связать S с P и Q.

Другие формы комплексной мощности (единицы в вольт-амперах, ВА) получаются из Z нагрузки , импеданса (единицы в омах, Ом).

$S=|I|^{2}Z={\frac {|V|^{2}}{Z^{*}}}$.

Следовательно, относительно треугольника мощности, реальная мощность (единицы измерения в ваттах, Вт) определяется как:

$P=|S|\cos {\varphi }=|I|^{2}R={\frac {|V|^{2}}{|Z|^{2}}}\times {R}$.

Для чисто резистивной нагрузки реальную мощность можно упростить до:

$P={\frac {|V|^{2}}{R}}$.

R обозначает сопротивление (единицы измерения в Омах, Ом) нагрузки.

Реактивная мощность (единицы измерения — вольт-ампер-реактивная, вар) определяется как:

$Q=|S|\sin {\varphi }=|I|^{2}X={\frac {|V|^{2}}{|Z|^{2}}}\times {X}$.

Для чисто реактивной нагрузки реактивную мощность можно упростить до:

$Q={\frac {|V|^{2}}{X}}$,

где X обозначает реактивное сопротивление (единицы измерения в Омах, Ом) нагрузки.

В результате комплексная мощность (единицы измерения в вольт-амперах, ВА) получается как

$S=P+jQ$,

и полную мощность (единицы измерения в вольт-амперах, ВА) как

$|S|={\sqrt {P^{2}+Q^{2}}}$.

Схематически они упрощены треугольником власти.

Коэффициент мощности

Основная статья: Коэффициент мощности

Отношение активной мощности к полной мощности в цепи называется коэффициентом мощности . Для двух систем, передающих одинаковое количество активной мощности, система с более низким коэффициентом мощности будет иметь более высокие циркулирующие токи из-за энергии, которая возвращается к источнику из накопителя энергии в нагрузке. Эти более высокие токи приводят к более высоким потерям и снижают общую эффективность передачи. Схема с более низким коэффициентом мощности будет иметь более высокую полную мощность и более высокие потери при том же количестве активной мощности. Коэффициент мощности равен 1,0, когда напряжение и ток совпадают по фазе . Оно равно нулю, когда ток опережает или отстает от напряжения на 90 градусов. Когда напряжение и ток сдвинуты по фазе на 180 градусов, коэффициент мощности отрицательный, и нагрузка подает энергию в источник (примером может служить дом с солнечными элементами на крыше, которые подают электроэнергию в электросеть, когда светит солнце). Коэффициенты мощности обычно указываются как «опережающие» или «запаздывающие», чтобы показать знак фазового угла тока по отношению к напряжению. Напряжение обозначается как база, с которой сравнивается угол тока, а это означает, что ток считается либо «опережающим», либо «запаздывающим» напряжением. Если сигналы имеют чисто синусоидальную форму, коэффициент мощности представляет собой косинус фазового угла ( $\varphi$) между синусоидальными сигналами тока и напряжения. В паспортах и ​​паспортных табличках оборудования коэффициент мощности часто обозначается сокращенно: « $\cos \phi$" по этой причине.

Пример: активная мощность составляет 700 Вт , а фазовый угол между напряжением и током составляет 45,6°. Коэффициент мощности составляет cos(45,6°) = 0,700 . Тогда полная мощность составит: 700 Вт/cos(45,6°) = 1000 ВА . Понятие рассеиваемой мощности в цепи переменного тока поясняется и иллюстрируется примером.

Например, коэффициент мощности 0,68 означает, что только 68 процентов общего подаваемого тока (по величине) фактически совершает работу; оставшийся ток не работает на нагрузке. Коэффициент мощности очень важен для подстанций энергетического сектора. В рамках национальной сети подотрасли должны иметь минимальный коэффициент мощности. В противном случае есть много потерь. В основном требуемые варьируются в пределах от 0,90 до 0,96 или более. Лучше коэффициент мощности меньше потерь.

Реактивная мощность

В цепи постоянного тока мощность, поступающая в нагрузку, пропорциональна произведению тока через нагрузку и падения потенциала на нагрузке. Мощность, возникающая из-за конденсатора или катушки индуктивности, называется реактивной мощностью. Это происходит из-за природы таких элементов, как катушки индуктивности и конденсаторы, переменного тока. Энергия течет в одном направлении от источника к нагрузке. В сети переменного тока напряжение и ток изменяются примерно синусоидально. Когда в цепи присутствует индуктивность или емкость, формы сигналов напряжения и тока не совпадают идеально. Поток мощности имеет две составляющие: одна компонента течет от источника к нагрузке и может выполнять работу при нагрузке; другая часть, известная как «реактивная мощность», возникает из-за задержки между напряжением и током, известной как фазовый угол, и не может выполнять полезную работу при нагрузке. Его можно рассматривать как ток, приходящий в неподходящее время (слишком поздно или слишком рано). Чтобы отличить реактивную мощность от активной, ее измеряют в единицах ". «вольт-ампер реактивный », или вар. Эти единицы можно упростить до ватт, но оставляют как вар, чтобы обозначить, что они не представляют собой фактическую производительность работы.

Энергия, запасенная в емкостных или индуктивных элементах сети, приводит к потоку реактивной мощности. Поток реактивной мощности сильно влияет на уровни напряжения в сети. Уровни напряжения и поток реактивной мощности должны тщательно контролироваться, чтобы обеспечить работу энергосистемы в приемлемых пределах. Метод, известный как реактивная компенсация, используется для уменьшения потока полной мощности в нагрузку за счет уменьшения реактивной мощности, подаваемой от линий электропередачи, и обеспечения ее локально. Например, для компенсации индуктивной нагрузки рядом с самой нагрузкой устанавливают шунтирующий конденсатор. Это позволяет всей реактивной мощности, необходимой нагрузке, поступать от конденсатора и не передавать ее по линиям передачи. Эта практика экономит энергию, поскольку уменьшает количество энергии, которую необходимо произвести коммунальному предприятию для выполнения того же объема работы. Кроме того, это позволяет создавать более эффективные конструкции линий электропередачи с использованием проводников меньшего размера или меньшего количества связанных проводников, а также оптимизировать конструкцию опор электропередачи.

Емкостная и индуктивная нагрузки

Запасенная энергия в магнитном или электрическом поле нагрузочного устройства, такого как двигатель или конденсатор, вызывает смещение между формами сигналов тока и напряжения. Конденсатор – это устройство, хранящее энергию в виде электрического поля. Когда через конденсатор протекает ток, накопление заряда вызывает появление противоположного напряжения на конденсаторе. Это напряжение увеличивается до достижения некоторого максимума, диктуемого структурой конденсатора. В сети переменного тока напряжение на конденсаторе постоянно меняется. Конденсатор противодействует этому изменению, заставляя ток опережать напряжение по фазе. Говорят, что конденсаторы «источники» реактивной мощности и, таким образом, вызывают опережающий коэффициент мощности.

Асинхронные машины сегодня являются одними из наиболее распространенных типов нагрузок в электроэнергетической системе. В этих машинах используются индукторы или большие катушки с проволокой для хранения энергии в форме магнитного поля. Когда на катушку изначально подается напряжение, индуктор сильно сопротивляется этому изменению тока и магнитного поля, что приводит к временной задержке достижения тока максимального значения. Это приводит к тому, что ток отстает от напряжения по фазе. Говорят, что индукторы «поглощают» реактивную мощность и, таким образом, вызывают запаздывающий коэффициент мощности. Адукционные генераторы могут генерировать или поглощать реактивную мощность и обеспечивать операторам системы определенный контроль над потоком реактивной мощности и, следовательно, напряжением. Поскольку эти устройства оказывают противоположное влияние на фазовый угол между напряжением и током, их можно использовать для «нейтрализации» эффектов друг друга. Обычно это принимает форму конденсаторных батарей, используемых для противодействия запаздыванию коэффициента мощности, вызванному асинхронными двигателями.

Контроль реактивной мощности

Основная статья: Контроль напряжения и управление реактивной мощностью

Генераторы, подключенные к передаче, обычно необходимы для поддержки потока реактивной мощности. Например, в системе электропередачи Соединенного Королевства в соответствии с требованиями Кодекса электросети генераторы должны обеспечивать номинальную мощность в пределах отставания коэффициента мощности 0,85 и опережения коэффициента мощности 0,90 на назначенных терминалах. Системный оператор будет выполнять коммутационные действия для поддержания безопасного и экономичного профиля напряжения, сохраняя при этом уравнение баланса реактивной мощности:

$\mathrm {Generator\ MVARs+System\ gain+Shunt\ capacitors=MVAR\ Demand+Reactive\ losses+Shunt\ reactors}$

«Коэффициент усиления системы » является важным источником реактивной мощности в приведенном выше уравнении баланса мощности, который генерируется емкостной природой самой сети передачи. Приняв решительные меры по переключению рано утром, до того, как спрос увеличится, можно максимизировать выгоду от системы на раннем этапе, помогая обеспечить безопасность системы на весь день. Чтобы сбалансировать уравнение, потребуется использование некоторого предаварийного реактивного генератора. Другие источники реактивной мощности, которые также будут использоваться, включают шунтирующие конденсаторы, шунтирующие реакторы, статические компенсаторы реактивной мощности и схемы управления напряжением.

Несбалансированные синусоидальные многофазные системы

Хотя активная мощность и реактивная мощность четко определены в любой системе, определение полной мощности для несбалансированных многофазных систем считается одной из самых спорных тем в энергетике. Первоначально кажущаяся власть возникла просто как показатель заслуг. Основные изложения этой концепции приписываются работам Стэнли « Явления замедления в индукционной катушке» (1888 г.) и ( Штейнмеца «Теоретическим элементам техники» 1915 г.). Однако с развитием трехфазного распределения электроэнергии стало ясно, что определение полной мощности и коэффициента мощности нельзя применять к несбалансированным многофазным системам . В 1920 году «Специальный объединенный комитет AIEE и Национальной ассоциации электрического освещения» собрался для решения этой проблемы. Они рассмотрели два определения.

$S_{A}=|S_{\mathrm {a} }|+|S_{\mathrm {b} }|+|S_{\mathrm {c} }|$

$\mathrm {pf} _{A}={P_{\mathrm {a} }+P_{\mathrm {b} }+P_{\mathrm {c} } \over S_{A}}$,

то есть арифметическая сумма полной мощности фазы; и

$S_{V}=|P_{\mathrm {a} }+P_{\mathrm {b} }+P_{\mathrm {c} }+j(Q_{\mathrm {a} }+Q_{\mathrm {b} }+Q_{\mathrm {c} })|$

$\mathrm {pf} _{V}={P_{\mathrm {a} }+P_{\mathrm {b} }+P_{\mathrm {c} } \over S_{V}}$,

то есть величину полной трехфазной комплексной мощности.

Комитет 1920 года не нашел консенсуса, и эта тема продолжала доминировать в дискуссиях. В 1930 году сформировался еще один комитет, который снова не смог решить вопрос. Стенограммы их дискуссий являются самыми длинными и противоречивыми, когда-либо опубликованными AIEE. Дальнейшего разрешения этой дискуссии удалось добиться лишь в конце 1990-х годов.

Новое определение, основанное на теории симметричных компонентов , было предложено в 1993 году Александром Эмануэлем для несбалансированной линейной нагрузки, питаемой асимметричными синусоидальными напряжениями:

$S={\sqrt {\left(|V_{\mathrm {a} }^{2}|+|V_{\mathrm {b} }^{2}|+|V_{\mathrm {c} }^{2}|\right)\left(|I_{\mathrm {a} }^{2}|+|I_{\mathrm {b} }^{2}|+|I_{\mathrm {c} }^{2}|\right)}}$

$\mathrm {pf} ={P^{+} \over S}$,

то есть корень из квадратов суммы линейных напряжений, умноженный на корень из квадратов сумм линейных токов. $P^{+}$ обозначает степень положительной последовательности:

$P^{+}=3|V^{+}||I^{+}|\cos {(\arg {(V^{+})}-\arg {(I^{+})})}$

$V^{+}$ обозначает вектор напряжения прямой последовательности, а $I^{+}$ обозначает вектор тока положительной последовательности.

Формулы действительных чисел

Идеальный резистор не накапливает энергии; поэтому ток и напряжение совпадают по фазе. Поэтому реактивной мощности нет. $P=S$ (используя соглашение о пассивных знаках ). Следовательно, для идеального резистора

$P=S=V_{\mathrm {RMS} }I_{\mathrm {RMS} }=I_{\mathrm {RMS} }^{2}R={\frac {V_{\mathrm {RMS} }^{2}}{R}}\,\!$.

Для идеального конденсатора или катушки индуктивности передача чистой мощности отсутствует; поэтому вся энергия является реактивной. Следовательно, для идеального конденсатора или катушки индуктивности:

${\begin{aligned}P&=0\\Q&=|S|=V_{\mathrm {RMS} }I_{\mathrm {RMS} }=I_{\mathrm {RMS} }^{2}|X|={\frac {V_{\mathrm {RMS} }^{2}}{|X|}}\end{aligned}}$.

где $X$ — реактивное сопротивление конденсатора или катушки индуктивности.

Если $X$ определяется как положительное значение для катушки индуктивности и отрицательное значение для конденсатора, то знаки модуля можно убрать из S и X и получить

$Q=I_{\mathrm {RMS} }^{2}X={\frac {V_{\mathrm {RMS} }^{2}}{X}}$.

Мгновенная мощность определяется как:

$p(t)=v(t)\,i(t)$,

где $v(t)$ и $i(t)$ представляют собой изменяющиеся во времени формы напряжения и тока.

Это определение полезно, поскольку оно применимо ко всем формам сигналов, независимо от того, синусоидальные они или нет. Это особенно полезно в силовой электронике, где распространены несинусоидальные сигналы.

В общем, инженеров интересует активная мощность, усредненная за период времени, будь то низкочастотный цикл сети или период переключения высокочастотного преобразователя мощности. Самый простой способ получить этот результат — взять интеграл мгновенного расчета за желаемый период:

$P_{\text{avg}}={\frac {1}{t_{2}-t_{1}}}\int _{t_{1}}^{t_{2}}v(t)\,i(t)\,\mathrm {d} t$.

Этот метод расчета средней мощности дает активную мощность независимо от гармонического содержания сигнала. В практических приложениях это можно было бы сделать в цифровой области, где расчет становится тривиальным по сравнению с использованием среднеквадратичного значения и фазы для определения активной мощности:

$P_{\text{avg}}={\frac {1}{n}}\sum _{k=1}^{n}V[k]I[k]$.

Многочастотные системы

Поскольку среднеквадратичное значение можно рассчитать для любой формы сигнала, на его основе можно рассчитать полную мощность. Для активной мощности на первый взгляд может показаться, что необходимо вычислить множество членов продукта и усреднить их все. Однако более подробное рассмотрение одного из этих терминов продукта дает очень интересный результат.

${\begin{aligned}&A\cos(\omega _{1}t+k_{1})\cos(\omega _{2}t+k_{2})\\={}&{\frac {A}{2}}\cos \left[\left(\omega _{1}t+k_{1}\right)+\left(\omega _{2}t+k_{2}\right)\right]+{\frac {A}{2}}\cos \left[\left(\omega _{1}t+k_{1}\right)-\left(\omega _{2}t+k_{2}\right)\right]\\={}&{\frac {A}{2}}\cos \left[\left(\omega _{1}+\omega _{2}\right)t+k_{1}+k_{2}\right]+{\frac {A}{2}}\cos \left[\left(\omega _{1}-\omega _{2}\right)t+k_{1}-k_{2}\right]\end{aligned}}$

Однако среднее по времени функции вида cos( ωt + k ) равно нулю при условии, что ω не равно нулю. Таким образом, единственными членами продукта, которые имеют ненулевое среднее значение, являются те, у которых частота напряжения и тока совпадают. Другими словами, можно рассчитать активную (среднюю) мощность, просто рассматривая каждую частоту отдельно и суммируя ответы. Более того, если предположить, что напряжение источника питания имеет одну частоту (что обычно так и есть), это показывает, что гармонические токи — это плохо. Они увеличат среднеквадратичный ток (поскольку будут добавлены ненулевые члены) и, следовательно, полную мощность, но не окажут влияния на передаваемую активную мощность. Следовательно, гармонические токи уменьшают коэффициент мощности. Гармонические токи можно уменьшить с помощью фильтра, установленного на входе устройства. Обычно это состоит либо из конденсатора (в зависимости от паразитного сопротивления и индуктивности источника питания), либо из сети конденсатор-индуктор. Активная коррекция коэффициента мощности Схема на входе, как правило, еще больше снижает гармонические токи и поддерживает коэффициент мощности ближе к единице.

См. также

• Война течений
• Передача электроэнергии
• Трансформатор
• Сетевое электричество
• Деформированная мощность

Внешние ссылки

• «Java-апплет AC Power»