Чириканье

Чтобы узнать о других значениях, см. Chirp (значения) .

Линейная форма сигнала с чирпом; синусоидальная волна, частота которой линейно увеличивается с течением времени

Чирп , — это сигнал которого частота увеличивается ( up-chirp ) или уменьшается ( down-chirp ) со временем. В некоторых источниках термин «чирп» используется как синоним «сигнала развертки» . Он обычно применяется в гидролокаторах , радарах и лазерных системах, а также в других приложениях, например, в средствах связи с расширенным спектром (см. ЛЧМ-расширенный спектр ). Этот тип сигнала имеет биологическое происхождение и возникает как явление, обусловленное дисперсией (нелинейной зависимостью между частотой и скоростью распространения компонентов волны). Обычно это компенсируется использованием согласованного фильтра, который может быть частью канала распространения. Однако в зависимости от конкретных показателей эффективности существуют более эффективные методы как для радара, так и для связи. Поскольку он использовался в радиолокации и космосе, он был принят также для стандартов связи. В автомобильных радарах его обычно называют сигналом с линейной частотной модуляцией (LFMW).

При использовании расширенного спектра устройства на поверхностных акустических волнах (ПАВ) часто используются для генерации и демодуляции чирпированных сигналов. В оптике ультракороткие . лазерные импульсы также демонстрируют чирп, который в оптических системах передачи взаимодействует с дисперсионными свойствами материалов, увеличивая или уменьшая общую дисперсию импульса по мере распространения сигнала Название является отсылкой к щебетанию птиц; см . пение птиц .

Определения

Основные определения здесь переводятся как общие физические величины: местоположение (фаза), скорость (угловая скорость), ускорение (шумность).Если форма волны определена как: $$x(t)=\sin \left(\phi (t)\right)$$

тогда мгновенная угловая частота ω определяется как фазовая скорость, определяемая первой производной фазы:где мгновенная обычная частота f является ее нормализованной версией: $$\omega (t)={\frac {d\phi (t)}{dt}},\,f(t)={\frac {\omega (t)}{2\pi }}$$

Наконец, мгновенная угловая чирпичность (символ γ ) определяется как вторая производная мгновенной фазы или первая производная мгновенной угловой частоты: $$\gamma (t)={\frac {d^{2}\phi (t)}{dt^{2}}}={\frac {d\omega (t)}{dt}}$$Угловая веселость измеряется в радианах на секунду в квадрате (рад/с). ² ); таким образом, это аналогично угловому ускорению .

Мгновенная обычная бодрость (символ c ) представляет собой нормализованную версию, определяемую как скорость изменения мгновенной частоты: $$c(t)={\frac {\gamma (t)}{2\pi }}={\frac {df(t)}{dt}}$$Обычное веселье имеет единицы квадратных обратных секунд (с ⁻² ); таким образом, это аналогично ускорению вращения .

Типы

Линейный

Спектрограмма линейного чирпа. График спектрограммы демонстрирует линейную скорость изменения частоты в зависимости от времени, в данном случае от 0 до 7 кГц, повторяющуюся каждые 2,3 секунды. Интенсивность графика пропорциональна содержанию энергии в сигнале на указанной частоте и времени.

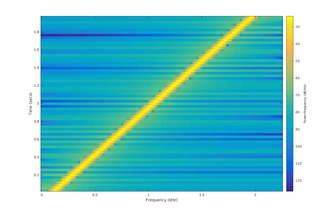
В линейно-частотном чирпе или просто линейном чирпе мгновенная частота $f(t)$ изменяется точно линейно со временем: $$f(t)=ct+f_{0},$$где $f_{0}$ — стартовая частота (в момент времени $t=0$) и $c$ — скорость чирпа, предполагаемая постоянной: $$c={\frac {f_{1}-f_{0}}{T}}={\frac {\Delta f}{\Delta t}}.$$

Здесь, $f_{1}$ конечная частота и $T$ это время, необходимое, чтобы вымести $f_{0}$ к $f_{1}$.

Соответствующая функция временной области для фазы любого осциллирующего сигнала является интегралом функции частоты, поскольку можно ожидать, что фаза будет расти как $\phi (t+\Delta t)\simeq \phi (t)+2\pi f(t)\,\Delta t$, т. е. что производная фазы есть угловая частота $\phi '(t)=2\pi \,f(t)$.

Для линейного чирпа это приводит к: $${\begin{aligned}\phi (t)&=\phi _{0}+2\pi \int _{0}^{t}f(\tau )\,d\tau \\&=\phi _{0}+2\pi \int _{0}^{t}\left(c\tau +f_{0}\right)\,d\tau \\&=\phi _{0}+2\pi \left({\frac {c}{2}}t^{2}+f_{0}t\right),\end{aligned}}$$

где $\phi _{0}$ является начальной фазой (в момент времени $t=0$). Таким образом, это также называется сигналом квадратичной фазы .

Соответствующая функция временной области для синусоидального линейного чирпа представляет собой синус фазы в радианах: $$x(t)=\sin \left[\phi _{0}+2\pi \left({\frac {c}{2}}t^{2}+f_{0}t\right)\right]$$

Экспоненциальный

Экспоненциальная форма сигнала с чирпом; синусоидальная волна, частота которой увеличивается экспоненциально с течением времени

Спектрограмма экспоненциального чирпа. Экспоненциальная скорость изменения частоты показана как функция времени, в данном случае от почти 0 до 8 кГц, повторяющаяся каждую секунду. На этой спектрограмме также виден спад частоты до 6 кГц после пика, что, вероятно, является артефактом конкретного метода, использованного для генерации сигнала.

В геометрическом чирпе , также называемом экспоненциальным чирпом , частота сигнала изменяется с течением времени в зависимости от геометрической зависимости. Другими словами, если выбраны две точки сигнала, $t_{1}$ и $t_{2}$, и интервал времени между ними $T=t_{2}-t_{1}$ остается постоянным, соотношение частот $f\left(t_{2}\right)/f\left(t_{1}\right)$ также будет постоянным.

В экспоненциальном чирпе частота сигнала изменяется экспоненциально в зависимости от времени: $$f(t)=f_{0}k^{\frac {t}{T}}$$где $f_{0}$ — стартовая частота (при $t=0$), и $k$ - скорость экспоненциального изменения частоты.

$$k={\frac {f_{1}}{f_{0}}}$$

Где $f_{1}$ конечная частота чирпа (при $t=T$).

В отличие от линейного чирпа, который имеет постоянный чирп, экспоненциальный чирп имеет экспоненциально возрастающую частоту.

Соответствующая временная функция для фазы экспоненциального чирпа представляет собой интеграл от частоты: $${\begin{aligned}\phi (t)&=\phi _{0}+2\pi \int _{0}^{t}f(\tau )\,d\tau \\&=\phi _{0}+2\pi f_{0}\int _{0}^{t}k^{\frac {\tau }{T}}d\tau \\&=\phi _{0}+2\pi f_{0}\left({\frac {Tk^{\frac {t}{T}}}{\ln(k)}}\right)\end{aligned}}$$где $\phi _{0}$ является начальной фазой (при $t=0$).

Соответствующая функция временной области для синусоидального экспоненциального чирпа представляет собой синус фазы в радианах: $$x(t)=\sin \left[\phi _{0}+2\pi f_{0}\left({\frac {Tk^{\frac {t}{T}}}{\ln(k)}}\right)\right]$$

Как и в случае с линейным чирпом, мгновенная частота экспоненциального чирпа состоит из основной частоты. $f(t)=f_{0}k^{\frac {t}{T}}$ сопровождаются дополнительными гармониками .

гиперболический

Гиперболические чирпы используются в радиолокационных приложениях, поскольку они показывают максимальную согласованную характеристику фильтра после искажения эффектом Доплера.

В гиперболическом чирпе частота сигнала изменяется гиперболически в зависимости от времени: $$f(t)={\frac {f_{0}f_{1}T}{(f_{0}-f_{1})t+f_{1}T}}$$

Соответствующая временная функция для фазы гиперболического чирпа представляет собой интеграл от частоты: $${\begin{aligned}\phi (t)&=\phi _{0}+2\pi \int _{0}^{t}f(\tau )\,d\tau \\&=\phi _{0}+2\pi {\frac {-f_{0}f_{1}T}{f_{1}-f_{0}}}\ln \left(1-{\frac {f_{1}-f_{0}}{f_{1}T}}t\right)\end{aligned}}$$где $\phi _{0}$ является начальной фазой (при $t=0$).

Соответствующая функция временной области для синусоидального гиперболического чирпа представляет собой синус фазы в радианах: $$x(t)=\sin \left[\phi _{0}+2\pi {\frac {-f_{0}f_{1}T}{f_{1}-f_{0}}}\ln \left(1-{\frac {f_{1}-f_{0}}{f_{1}T}}t\right)\right]$$

Поколение

Чирп-сигнал может быть сгенерирован с помощью аналоговой схемы с помощью генератора, управляемого напряжением (ГУН), и линейно или экспоненциально нарастающего управляющего напряжения . Его также можно генерировать в цифровом виде с помощью цифрового сигнального процессора (DSP) и цифро-аналогового преобразователя (DAC), используя прямой цифровой синтезатор (DDS) и изменяя шаг генератора с числовым управлением. Его также можно генерировать с помощью YIG-генератора .

Связь с импульсным сигналом

Чирповые и импульсные сигналы и их (избранные) спектральные составляющие . Внизу даны четыре монохроматические составляющие, синусоидальные волны разной частоты. Красная линия на волнах показывает относительный сдвиг фазы по отношению к другим синусоидальным волнам, возникающий из-за характеристики чирпа. Анимация шаг за шагом удаляет фазовый сдвиг (как и в случае с согласованной фильтрацией ), что приводит к появлению синхроимпульса , когда относительного фазового сдвига не осталось.

ЛЧМ-сигнал имеет тот же спектральный состав, что и импульсный сигнал . Однако, в отличие от импульсного сигнала, спектральные составляющие ЛЧМ-сигнала имеют разные фазы. т. е. их спектры мощности одинаковы, но фазовые спектры различны. Дисперсия среды распространения сигнала может привести к непреднамеренному преобразованию импульсных сигналов в чирпы ( Уистлер ). С другой стороны, многие практические приложения, такие как усилители чирпированных импульсов или системы эхолокации, используйте чирп-сигналы вместо импульсов из-за их более низкого отношения пиковой мощности к средней (PAPR).

Использование и возникновение

Чирп-модуляция

Чирп-модуляция, или линейная частотная модуляция для цифровой связи, была запатентована Сидни Дарлингтоном в 1954 году, а значительная последующая работа была выполнена Винклером в 1962 году. В этом типе модуляции используются синусоидальные сигналы, мгновенная частота которых линейно увеличивается или уменьшается с течением времени. Эти сигналы обычно называют линейными чирпами или просто чирпами.

Следовательно, скорость изменения их частоты называется скоростью чирпа . При двоичной ЛЧМ-модуляции двоичные данные передаются путем преобразования битов в ЛМ-сигналы с противоположными скоростями. Например, в течение одного битового периода «1» назначается ЛЧМ с положительной скоростью a, а «0» — ЛЧМ с отрицательной скоростью − a . ЛЧМ-сигналы широко используются в радиолокационных приложениях, в результате чего современные источники передачи и согласованные фильтры доступны для приема линейных ЛЧМ-сигналов.

(а) При обработке изображений прямая периодичность встречается редко, а скорее встречается периодичность в перспективе. (б) Повторяющиеся структуры, такие как чередование темного пространства внутри окон и светлого пространства белого бетона, «чириканье» (увеличение частоты) вправо. (c) Таким образом, наиболее подходящим чирпом для обработки изображений часто является проективный чирп.

Преобразование чирплета

Основная статья: Преобразование Chirplet

Другой вид щебетания — это проективный щебет, имеющий форму: $$g=f\left[{\frac {a\cdot x+b}{c\cdot x+1}}\right],$$имеющий три параметра a (масштаб), b (перевод) и c (бодрость). Проективный чирплет идеально подходит для обработки изображений и формирует основу для проективного чирплетного преобразования .

Ключевой щебет

Изменение частоты кода Морзе от желаемой частоты из-за плохой стабильности радиочастотного генератора известно как чирп . а в системе RST к нему добавляется буква «С».

См. также

• Chirp Spectrum - Анализ частотного спектра чирп-сигналов
• Chirp-сжатие — дополнительная информация о методах сжатия.
• Расширенный спектр Chirp . Часть стандарта беспроводной связи IEEE 802.15.4a CSS.
• Чирикающее зеркало
• Усиление чирпированных импульсов
• Преобразование чирплета — представление сигнала, основанное на семействе локализованных функций чирплета.
• Радар непрерывного действия
• Дисперсия (оптика)
• Сжатие импульсов
• Распространение радиосигнала § Измерение распространения ВЧ

Внешние ссылки

• Онлайн-генератор звуковых сигналов (вывод файла WAV)
• Сонар CHIRP на FishFinder
• Сонар CHIRP на FishFinder