Теорема Гуи–Стодолы

В термодинамике и теплофизике теорема Гуи -Стодолы является важной теоремой для количественного определения необратимости в открытой системе и помогает в эксергетическом анализе термодинамических процессов . Он утверждает, что скорость, с которой работа теряется во время процесса или с которой разрушается эксергия, пропорциональна скорости, с которой энтропия генерируется , и что коэффициент пропорциональности - это температура окружающего резервуара тепла. В литературе теорема часто появляется в несколько модифицированном виде, изменяя коэффициент пропорциональности.

Теорема названа совместно в честь французского физика Жоржа Гуи и словацкого физика Орела Стодолы , которые продемонстрировали теорему в 1889 и 1905 годах соответственно. Гуи использовал его при работе над эксергией и полезной энергией, а Стодола — при работе над паровыми и газовыми двигателями.

Обзор

Теорема Гуи-Стодолы часто применяется к открытой термодинамической системе, которая может обмениваться теплом с некоторыми тепловыми резервуарами . Это справедливо как для систем, которые не могут обмениваться массой, так и для систем, масса которых может входить и выходить.

Система вместе с резервуарами

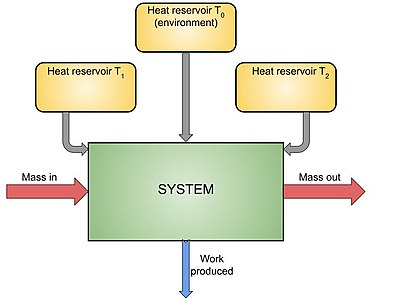
Понаблюдайте за такой системой, как показано на изображении, когда она проходит какой-то процесс . Он находится в контакте с несколькими резервуарами, один из которых имеет температуру $T_{0}$, является резервуаром окружающей среды. В ходе этого процесса система производит работу и генерирует энтропию. В этих условиях теорема имеет два общих вида.

Форма работы

Обратимая работа – это максимальная полезная работа, которую можно получить. $W_{rev}=W_{max}$и может быть полностью использован только в идеальном обратимом процессе . Необратимый процесс производит некоторую работу $W_{actual}$, что меньше, чем $W_{rev}$. Потерянная работа тогда $W_{lost}=W_{rev}-W_{actual}$; другими словами, $W_{lost}$ — это работа, которая была потеряна или не использована в ходе процесса из-за необратимости. Что касается потерянной работы, теорема обычно гласит: $${\dot {W}}_{lost}=T_{0}{\dot {S_{g}}}$$где ${\dot {W}}_{lost}$ - это скорость, с которой теряется работа, и ${\dot {S_{g}}}$ это скорость, с которой генерируется энтропия. Производные по времени обозначены точками. Теорема, как сказано выше, справедлива только для всей термодинамической Вселенной — системы вместе с ее окружением вместе: $${\dot {W}}_{lost,tot}=T_{0}{\dot {S}}_{g,tot}$$где индекс «tot» обозначает общее количество произведенных внутри или во всей Вселенной.

Обратите внимание, что ${\dot {W}}_{lost}$ Это относительная величина, поскольку она измеряется по отношению к конкретному термальному резервуару. В приведенных выше уравнениях ${\dot {W}}_{lost}$ определяется относительно резервуара окружающей среды, при $T_{0}$. При сравнении реального процесса с идеальным обратимым процессом между теми же конечными точками (чтобы оценить $W_{rev}$, чтобы найти значение $W_{lost}$), только тепловое взаимодействие с эталонным резервуаром $T_{0}$ допускается варьировать. Тепловые взаимодействия между системой и другими резервуарами сохраняются прежними. Итак, если другой эталонный резервуар $T_{ref}$ выбрано, теорема будет выглядеть так: ${\dot {W}}_{lost,tot}=T_{ref}{\dot {S}}_{g,tot}$, где на этот раз ${\dot {W}}_{lost}$ это по отношению к $T_{ref}$, а в соответствующем обратимом процессе только тепловое взаимодействие с $T_{ref}$ отличается.

Путем интегрирования по времени существования процесса теорему также можно выразить через конечные количества, а не скорости: ${W}_{lost,tot}=T_{0}{S}_{g,tot}$.

Адиабатический случай

Теорема справедлива и для адиабатических процессов . То есть для закрытых систем, не находящихся в тепловом контакте с какими-либо теплоемкими резервуарами.

Как и в неадиабатическом случае, потерянная работа измеряется относительно некоторого эталонного резервуара. $T_{0}$. Несмотря на то, что сам процесс является адиабатическим, соответствующий обратимый процесс может не быть адиабатическим и может потребовать теплообмена с эталонным резервуаром. Таким образом, это можно рассматривать как частный случай приведенного выше утверждения теоремы – адиабатический процесс – это такой, при котором тепловые взаимодействия со всеми резервуарами равны нулю, а в обратимом процессе – только тепловое взаимодействие с эталонным тепловым резервуаром. может быть разным.

Адиабатический случай теоремы справедлив и для другой формулировки теоремы, представленной ниже.

Эксергетическая форма

Эксергия системы — это максимальное количество полезной работы, которую система может произвести в ходе процесса , приводящего ее в равновесие с окружающей средой, или количество доступной энергии. Во время необратимого процесса , такого как теплообмен с резервуарами, эксергия разрушается. В общем случае теорема утверждает, что $${\dot {\psi }}_{d}=T_{0}{\dot {S_{g}}}$$где ${\dot {\psi }}_{d}$ - это скорость, с которой разрушается эксергия, и ${\dot {S_{g}}}$ это скорость, с которой генерируется энтропия. Как и выше, производные по времени обозначены точками.

В отличие от формулировки потерянной работы, эта версия теоремы справедлива как для системы (управляющего объема), так и для ее окружения (окружающей среды и тепловых резервуаров) отдельно: $${\dot {\psi }}_{d,sys}=T_{0}{\dot {S}}_{g,sys}$$и $${\dot {\psi }}_{d,surr}=T_{0}{\dot {S}}_{g,surr}$$где индекс «sys» обозначает количества, производимые внутри или самой системой, а «surr» внутри или в окружающей среде. Следовательно, суммируя эти две формы, теорема справедлива и для термодинамической Вселенной в целом: $${\dot {\psi }}_{d,tot}={\dot {\psi }}_{d,sys}+{\dot {\psi }}_{d,surr}=T_{0}{\dot {S}}_{g,sys}+T_{0}{\dot {S}}_{g,surr}=T_{0}{\dot {S}}_{g,tot}$$где индекс «tot» обозначает общие количества всей Вселенной.

Таким образом, эксергетическая формулировка теоремы менее ограничена, поскольку ее можно применять к различным областям отдельно. Тем не менее, форма работы используется чаще.

Доказательство теоремы в обеих формах использует первый закон термодинамики , записывая члены ${\dot {W}}_{lost}$, ${\dot {\psi }}_{d}$, и ${\dot {S_{g}}}$ в соответствующих регионах и их сравнение.

Модифицированный коэффициент и эффективная температура

Во многих случаях предпочтительнее использовать в рабочей форме несколько модифицированный вариант теоремы Гуи-Стодолы, где $T_{0}$ заменяется некоторой эффективной температурой. Когда это делается, это часто расширяет сферу применения теоремы и адаптирует ее для применимости к большему количеству систем или ситуаций. Например, приведенные ниже поправки необходимы только в том случае, если система обменивается теплом с более чем одним резервуаром - если она обменивается теплом только при температуре окружающей среды. $T_{0}$, справедлива приведенная выше простая форма. Кроме того, модификации могут изменить обратимый процесс, с которым сравнивается реальный процесс при расчете. ${\dot {W}}_{lost}$.

Модифицированная теорема тогда читается $${\dot {W}}_{lost}=T_{eff}{\dot {S_{g}}}$$где $T_{eff}$ – эффективная температура.

Для проточного процесса пусть $s_{1}$ обозначают удельную энтропию (энтропию на единицу массы) на входе, куда поступает масса, и $s_{2}$ удельная энтропия на выходе, куда вытекает масса. Аналогично обозначим удельную энтальпию через $h_{1}$ и $h_{2}$. В этом случае вход и выход функционируют как начальное и конечное состояния процесса: масса входит в систему в начальном состоянии (вход, обозначенный «1»), подвергается некоторому процессу, а затем выходит в конечном состоянии (выход , с индексом «2»).

Затем этот процесс сравнивается с обратимым процессом с тем же начальным состоянием, но с (возможно) другим конечным состоянием. Теоретическая удельная энтропия и энтальпия после этого идеального изэнтропического процесса определяются выражением $s_{2,rev}$ и $h_{2,rev}$, соответственно. Когда реальный процесс сравнивается с этим теоретическим обратимым процессом и ${\dot {W}}_{lost}$ оценивается, правильная эффективная температура определяется выражением $$T_{eff}={\frac {h_{2}-h_{2,rev}}{s_{2}-s_{2,rev}}}$$В общем, $T_{eff}$ находится где-то посередине между конечной температурой реального процесса $T_{2}$ и конечная температура в теоретическом обратимом процессе $T_{2,rev}$.

Это уравнение, приведенное выше, иногда можно упростить. Если и давление , и удельная теплоемкость остаются постоянными, то изменения энтальпии и энтропии можно записать через температуры: $$T_{eff}={\frac {T_{2}-T_{2,rev}}{\ln T_{2}-\ln T_{2,rev}}}={\frac {T_{2}-T_{2,rev}}{\ln {\frac {T_{2}}{T_{2,rev}}}}}$$Однако важно отметить, что эта версия теоремы не связывает точные значения, как в исходной теореме. В частности, при сравнении реального процесса с обратимым модифицированная версия позволяет различать конечное состояние этих двух процессов. В этом отличие от исходной версии, в которой обратимый процесс построен таким образом, чтобы конечные состояния были одинаковыми.

Приложения

В общем, теорема Гуи-Стодолы используется для количественной оценки необратимости в системе и проведения эксергетического анализа. То есть позволяет взять термодинамическую систему и лучше понять, насколько она неэффективна (с точки зрения энергии), сколько работы теряется, сколько есть возможностей для улучшения и где. По сути, второй закон термодинамики гласит, что энтропия системы только возрастает. Со временем термодинамические системы имеют тенденцию набирать энтропию и терять энергию (при приближении к равновесию): таким образом, энтропия «каким-то образом» связана с тем, сколько эксергии или потенциала полезной работы имеет система. Теорема Гуи-Стодолы обеспечивает конкретную связь. По большей части именно так эта теорема и используется — для поиска и количественной оценки неэффективности системы.

Поточные процессы

Основная статья: Потоковый процесс

Процесс потока — это тип термодинамического процесса , при котором вещество течет внутрь и наружу в открытую систему, называемую контрольным объемом . Такой процесс может быть устойчивым , то есть материя и энергия, входящие в систему и выходящие из нее, постоянны во времени. Он также может быть нестационарным или переходным, что означает, что потоки могут меняться и различаться в разное время.

Многие доказательства теоремы демонстрируют ее именно для проточных систем. Таким образом, теорема особенно полезна при проведении эксергетического анализа таких систем.

Сжатие и поглощение пара

См. Также: Тепловой насос и холодильный цикл , Охлаждение § Циклическое охлаждение и Паросжатие охлаждения.

Теорема Гуи-Стодолы часто применяется к холодильным циклам . Это термодинамические циклы или механические системы, в которых можно использовать внешнюю работу для перемещения тепла от источников с низкой температурой к поглотителям с высокой температурой или наоборот. В частности, теорема полезна при анализе с компрессией пара и абсорбцией пара циклов охлаждения .

Теорема может помочь определить, какие компоненты системы имеют большую необратимость и сколько эксергии они разрушают. Его можно использовать, чтобы определить, при каких температурах производительность оптимальна или какой размер системы следует построить. В целом, то есть теорема Гуи-Стодолы является инструментом для поиска и количественной оценки неэффективности системы и может указать, как их минимизировать - это цель эксергетического анализа. Когда теорема используется для этих целей, ее обычно применяют в модифицированной форме.

В экологии

Макроскопически теорема может быть полезна с экологической точки зрения, в экофизике. Экосистема – это сложная система , в которой взаимодействует множество факторов и компонентов, как биотических, так и абиотических. Теорема Гуи-Стодолы позволяет определить, сколько энтропии генерируется каждой частью системы или сколько работы теряется. Если в экосистему вмешивается человек, то, продолжит ли экосистема существовать или исчезнет, ​​может зависеть от того, сколько необратимых явлений она может выдержать. Количество генерируемой энтропии или объем работы, которую может выполнить система, могут различаться. Следовательно, два разных состояния (например, здоровый лес и состояние, подвергшееся значительному вырубке лесов) одной и той же экосистемы можно сравнивать с точки зрения генерации энтропии, и это можно использовать для оценки устойчивости экосистемы под воздействием человека.

В биологии

Теорема полезна и в более микроскопическом масштабе, в биологии . Живые системы, такие как клетки , можно анализировать термодинамически. Это довольно сложные системы, в которых происходит множество преобразований энергии и они часто теряют тепло. Следовательно, теорема Гуи-Стодолы может быть полезна в определенных ситуациях для проведения эксергетического анализа таких систем. В частности, это может помочь выявить различия между здоровыми и больными клетками.

Как правило, теорема может найти применение в областях биомедицины или там, где биология и физика пересекаются, например, в биохимической инженерии, термодинамике .

Вариационный принцип

Вариационный принцип в физике, такой как принцип наименьшего действия или принцип Ферма в оптике, позволяет описать систему глобально и решить ее с помощью вариационного исчисления . В термодинамике такой принцип позволил бы использовать лагранжеву формулировку. Теорема Гуи-Стодолы может быть использована в качестве основы для такого вариационного принципа в термодинамике. Доказано, что он удовлетворяет необходимым условиям.

Это фундаментально отличается от большинства других применений теоремы — здесь она применяется не для обнаружения компонентов с необратимостью или потерей эксергии, а, скорее, помогает дать более общую информацию о системе.