Динамический прямоугольник
Динамический прямоугольник — это прямоугольная четырехсторонняя фигура ( прямоугольник ) с динамической симметрией , что в данном случае означает, что соотношение сторон (ширина, разделенная на высоту) является выдающимся значением динамической симметрии , системы пропорций и естественного дизайна. методология, описанная в Джея Хэмбиджа книгах . Эти динамические прямоугольники начинаются с квадрата , который расширяется (с помощью ряда дуг и точек пересечения) для формирования желаемой фигуры, которая может быть золотым прямоугольником (1:1,618...), прямоугольником 2:3, двойным прямоугольником. квадрат (1:2) или корневой прямоугольник (1: √ φ , 1: √ 2 , 1: √ 3 , 1: √ 5 и т. д.). [1] [2] [3]
Корневые прямоугольники
[ редактировать ]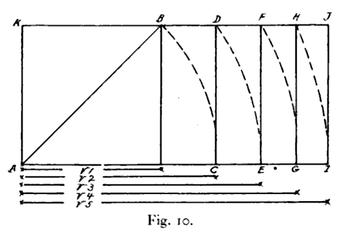
Корневой прямоугольник — это прямоугольник , в котором отношение большей стороны к меньшей является квадратным корнем целого числа , например √ 2 , √ 3 и т. д. [2]
Прямоугольник с корнем 2 (ACDK на рис. 10) строится путем продления двух противоположных сторон квадрата до длины его диагонали. Прямоугольник с корнем 3 создается путем удлинения двух более длинных сторон прямоугольника с корнем 2 до длины диагонали прямоугольника с корнем 2. Каждый последующий корневой прямоугольник создается путем удлинения более длинных сторон корневого прямоугольника до длины его диагонали. [4]
Характеристики
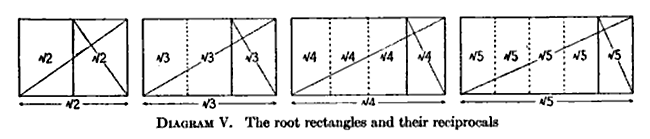
[ редактировать ]- Когда прямоугольник с корнем N делится на N равных прямоугольников путем деления длинного края на N сегментов, полученные фигуры сохраняют пропорцию корня N (как показано выше). [5]
- Прямоугольник с корнем-3 также называется шеститоном . [6] а его короткая и длинная стороны пропорционально эквивалентны стороне и диаметру шестиугольника . [7]
- Поскольку 2 — это квадратный корень из 4, прямоугольник с корнем 4 имеет пропорцию 1:2, что означает, что он эквивалентен двум квадратам, расположенным рядом. [7]
- Прямоугольник с корнем 5 связан с золотым сечением (φ). Более длинная сторона равна один плюс два раза 1/φ (0,618...). [7]
Корневой прямоугольник φ
[ редактировать ]
Прямоугольник root-φ является динамическим прямоугольником, но не корневым прямоугольником. Его диагональ равна φ, умноженной на длину меньшей стороны. Если прямоугольник с корнем φ разделить диагональю, в результате получатся два конгруэнтных треугольника Кеплера .
Джей Хэмбидж
[ редактировать ]Джей Хэмбидж , как часть своей теории динамической симметрии, включает корневые прямоугольники в то, что он называет динамическими прямоугольниками , которые имеют иррациональные и геометрические дроби в качестве отношений, таких как золотое сечение или квадратные корни. Хэмбидж отличает их от прямоугольников с рациональными пропорциями, которые он называет статическими прямоугольниками . [3] По его словам, прямоугольники с корнем 2, 3, 4 и 5 часто встречаются в готическом и классическом греческом и римском искусстве, объектах и архитектуре, в то время как прямоугольники с соотношением сторон, превышающим корень 5, редко встречаются в человеческих проектах. [4]
По мнению Матилы Гики , динамические прямоугольники Хэмбиджа
может создавать самые разнообразные и удовлетворительные гармонические (согласные, связанные симметрией) подразделения и комбинации, и это происходит за счет очень простого процесса [...] рисования внутри выбранного прямоугольника диагонали и перпендикуляра к ней из одного из двух оставшихся вершин (таким образом разделяя поверхность на обратный прямоугольник и его гномон) и рисуя любую сеть параллелей и перпендикуляров к сторонам и диагоналям. Это автоматически создает поверхности, соответствующие характерным пропорциям исходного прямоугольника, а также позволяет избежать (снова автоматически) смешивания антагонистических тем, таких как √ 2 и √ 3 или √ 5 . √ 5 и Φ, наоборот, не антагонистичны, а созвучны, также с √ Φ , Φ 2 , и так далее. [3]
12 ортогонов Версина
[ редактировать ]Согласно книге Вольфганга фон Версина « Книга прямоугольников, пространственный закон и жесты описанных ортогонов» (1956), набор из 12 особых ортогонов (от греч. ορθος , ортос , «прямой»). [9] и γονια , гония , «угол»; «прямоугольная фигура», которая, как следствие, бывает прямоугольной и четырехугольной. [10] )исторически использовался художниками, архитекторами и каллиграфами для управления размещением и взаимодействием элементов в дизайне. [3] [11] Эти ортогоны: [12]
- Квадрат (1:1 или 1: √ 1 )
- Диагональ (1: √ 2 )
- Гектон или шеститон (1: √ 3 )
- Доппельквадрат (1:2 или 1: √ 4 )
- Гемиолион (2:3)
- Аурон ( золотой прямоугольник , 1: φ )
- Полудиагон (1:½ √ 5 )
- Пентон (1: √ φ )
- Трио (1:⅔ √ 3 )
- Четырехугольник (1:(1+ √ 2 )/2)
- Биаурон (1:2φ)
- Бипентон (1:2 √ 5-2 √ 5 )
Книга Вольфганга фон Версина включает в себя необычную копию текста 1558 года ( Возрождение ) со схемами семи из 12 ортогонов и приглашением из отрывка обратить пристальное внимание, поскольку «древние» архитекторы считали, что «ничто не превосходит эти пропорции», поскольку «вещь чистейшей абстракции». [13]
Все 12 ортогонов, образуя вместе, образуют единое целое: квадрат, который превращается в двойной квадрат. [14]
Пожалуй, самым популярным среди ортогонов является аурон или золотой прямоугольник , который получается путем проецирования диагонали, идущей от средней точки стороны квадрата, к одной из противоположных вершин, пока она не совпадет со средней точкой.
Четыре из этих ортогонов являются гармоническими прямоугольниками: прямоугольник, или с корнем 2 прямоугольник , получается путем проецирования диагонали квадрата; шеститона корня , гектона или -3 прямоугольник получается путем проецирования диагонали диагонали; двойной квадрат или с корнем из 4 прямоугольник получается путем проецирования диагонали гектона; Прямоугольник корнем 5 с получается путем проецирования диагонали двойного квадрата (или путем проецирования на 180 ° обеих диагоналей, идущих от средней точки стороны квадрата к противоположным вершинам).
Две самые сложные из этих фигур: пентон сторона , с пропорциями 1: √ φ относится к сечению золотой пирамиды , длинная сторона бипентона равна меньшей, умноженной на две трети квадратного корня из трех, длинная биаурона равна √ 5 - в 1 или 2τ раза короче.
Четырехугольник связан с диагональю в том смысле , что его длинная сторона получается путем проецирования диагонали четверти квадрата. Трион имеет высоту равностороннего треугольника и ширину стороны. ( Более длинная сторона полудиагона 1:½ √ 5 ) равна половине длины прямоугольника с корнем 5 и получается путем проецирования диагонали половины квадрата до тех пор, пока она не станет перпендикулярной началу координат.
Помимо квадрата и двойного квадрата, единственным статическим прямоугольником, включенным в список, является гемиолион , который получается путем проецирования на 90° или 180° половины стороны квадрата.
Построение ортогона
[ редактировать ]Размеры ортогонов относятся друг к другу и к ортогону в целом. По этой причине использование ортогонов в качестве шаблона или базовой структуры представляет интерес для художников, архитекторов и дизайнеров. [15]
Ортогоны всегда начинаются с квадрата, любого квадрата. После построения отдельного ортогона определяются дополнительные связанные измерения (малые, средние, большие). Эти измерения затем можно использовать при проектировании (живопись, архитектура, керамика, мебель, каллиграфия, автомобили и т. д.).
В книге Версина есть очень подробные объяснения создания отдельных ортогонов. [16] Полученные измерения затем применяются при проектировании. Произведения Джорджо Моранди иллюстрируют, как измерения разных размеров (полученные из ортогона) могут создать визуальную гармонию.
Ортогоны и дизайн
[ редактировать ]Использование размеров, связанных с ортогоном, в качестве базовой системы (или шаблона для проекта) гарантирует, что различные части будут относиться к проекту в целом. Марк Витрувий Поллион в третьей книге « De Architectura » (известной в настоящее время как «Десять книг по архитектуре») объясняет:
«Поэтому, поскольку природа спроектировала человеческое тело так, что его члены должным образом пропорциональны каркасу в целом, кажется, что древние имели веские основания для своего правила, согласно которому в совершенных зданиях различные члены должны находиться в точно симметричных отношениях с телом человека. Поэтому, передавая нам надлежащее устройство зданий всех видов, они особенно тщательно делали это в случае храмов богов, зданий, достоинства и недостатки которых обычно сохраняются навсегда».
Рисунок Леонардо «Витрувианский человек» является иллюстрацией концепции частей, относящихся к произведению в целом. [17]
Ссылки
[ редактировать ]- ^ СКИННЕР, Стивен, Сакральная геометрия, расшифровывающая код , Нью-Йорк: Sterling Publishing Company, 2006, стр. 53.
- ↑ Перейти обратно: Перейти обратно: а б с Джей Хэмбидж (1920) [1920]. Динамическая симметрия: греческая ваза (перепечатка оригинального издания издательства Йельского университета). Уайтфиш, Монтана: Издательство Кессинджер. стр. 19–29 . ISBN 0-7661-7679-7 .
Корневые прямоугольники динамической симметрии.
- ↑ Перейти обратно: Перейти обратно: а б с д Матила Гика (1977). Геометрия искусства и жизни . Публикации Курьера Дувра. стр. 126–127 . ISBN 9780486235424 .
- ↑ Перейти обратно: Перейти обратно: а б Джей Хэмбидж. (1926, 1948, 1967) Элементы динамической симметрии . Публикации Курьера Дувра. стр. 9–10.
- ^ Эндрю Хаслам (2006). Книжный дизайн . Издательство Лоуренса Кинга. стр. 48–49 . ISBN 1-85669-473-9 .
корень-прямоугольник.
- ^ Вим Мюллер (2001) Порядок и смысл в дизайне . Издательство Лемма, с. 49.
- ↑ Перейти обратно: Перейти обратно: а б с Кимберли Элам (2001). Геометрия дизайна: исследования пропорций и композиции . Принстонская архитектурная пресса. стр. 34–41. ISBN 1-56898-249-6 .
- ^ Лейси Дэвис Кэски (1922). Геометрия греческих ваз: аттические вазы в Музее изящных искусств, проанализированные на основе принципов пропорций, открытых Джеем Хэмбиджем . Музей изящных искусств, Бостон.
- ^ «Орто-» , Оксфордский словарь современного английского языка , Оксфорд: Oxford University Press, 1998, стр. 627, 1071 стр.
- ^ КЕРТИС, Томас, Лондонская энциклопедия , 1829, стр. 356.
- ^ ВЕРСИН, Вольфганг Фон, Книга закона прямоугольника и жеста пространственного диска Отогона. Die Orthogone-scheibe ( Книга прямоугольников, пространственного закона и жестов описанных ортогонов. Описанные ортогоны ), Равенсбург: Otto Maier Verlag Publishers, 1956
- ^ ВЕРСИН, стр. 83.
- ^ ВЕРСИН, соч. цит., с. 36
- ^ ВЕРСИН, стр. 80.
- ^ «Построение тетради Вселенной. Том 4: Динамические прямоугольники» .
- ^ ВЕРСИН, стр. 82-85.
- ^ ХЕМЕНВЭЙ, стр. 95.
Дальнейшее чтение
[ редактировать ]- Хеменвей, Прия; Божественная Пропорция, Фи в Искусстве, Природе и Науке; 2005, Sterling Publishing Co., Inc, Нью-Йорк, Нью-Йорк.
