Лемма о покрытии Виталия

В математике лемма о покрытии Витали представляет собой комбинаторный и геометрический результат, обычно используемый в теории меры евклидовых пространств . Эта лемма представляет собой промежуточный шаг, представляющий самостоятельный интерес, в доказательстве теоремы Витали о накрытии . Теорема о покрытии принадлежит итальянскому математику Джузеппе Витали . Теорема утверждает, что можно покрыть с точностью до пренебрежимо Лебега множества заданное подмножество E из R ^д несвязным семейством, выделенным из Витали накрытия E .

Виталий, покрывающий лемму

Визуализация леммы в $\mathbb {R} ^{1}$.

Вверху: коллекция мячей; зеленые шарики — это непересекающаяся подколлекция. Внизу: подколлекция с трехкратным радиусом охватывает все шары.

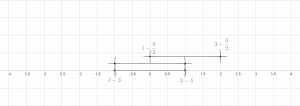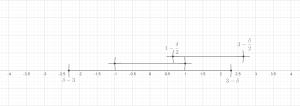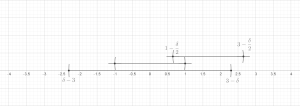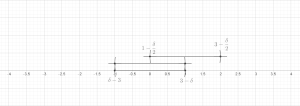
Есть две основные версии леммы: конечная версия и бесконечная версия. Обе леммы могут быть доказаны в общей ситуации метрического пространства , обычно эти результаты применяются к частному случаю евклидова пространства. $\mathbb {R} ^{d}$. В обеих теоремах мы будем использовать следующие обозначения: если ${\textstyle B=B(x,r)}$ это мяч и $c\geq 0$, мы напишем $cB$ для мяча ${\textstyle B(x,cr)}$.

Конечная версия

Теорема (лемма о конечном покрытии). Позволять $B_{1},\dots ,B_{n}$ — любой конечный набор шаров, содержащийся в произвольном метрическом пространстве. Тогда существует подколлекция $B_{j_{1}},B_{j_{2}},\dots ,B_{j_{m}}$ из этих шаров, которые не пересекаются и удовлетворяют $$B_{1}\cup B_{2}\cup \dots \cup B_{n}\subseteq 3B_{j_{1}}\cup 3B_{j_{2}}\cup \dots \cup 3B_{j_{m}}.$$Доказательство. Не ограничивая общности, мы предполагаем, что набор шаров не пуст; т. е. n > 0. Пусть $B_{j_{1}}$ быть шаром наибольшего радиуса. Индуктивно предположим, что $B_{j_{1}},\dots ,B_{j_{k}}$ были выбраны. Если есть какой-то мяч $B_{1},\dots ,B_{n}$ это не пересекается с $B_{j_{1}}\cup B_{j_{2}}\cup \dots \cup B_{j_{k}}$, позволять $B_{j_{k+1}}$ быть таким шаром максимального радиуса (произвольно разрывая связи), в противном случае мы полагаем m := k и прекращаем индуктивное определение.

Теперь установите ${\textstyle X:=\bigcup _{k=1}^{m}3\,B_{j_{k}}}$. Осталось показать, что $B_{i}\subset X$ для каждого $i=1,2,\dots ,n$. Это ясно, если $i\in \{j_{1},\dots ,j_{m}\}$. В противном случае обязательно существует какое-то $k\in \{1,\dots ,m\}$ такой, что $B_{i}$ пересекает $B_{j_{k}}$. Выбираем минимально возможное $k$ и обратите внимание, что радиус $B_{j_{k}}$ по крайней мере так же велик, как и $B_{i}$. следует , что неравенства треугольника Тогда из $B_{i}\subset 3\,B_{j_{k}}\subset X$, по мере необходимости. Это завершает доказательство конечной версии.

Бесконечная версия

Теорема (лемма о бесконечном покрытии). Позволять $\mathbf {F}$ — произвольный набор шаров в сепарабельном метрическом пространстве такой, что $$R:=\sup \,\{\mathrm {rad} (B):B\in \mathbf {F} \}<\infty$$ где $\mathrm {rad} (B)$ обозначает радиус шара B . Тогда существует счетное подмножество $\mathbf {G} \subset \mathbf {F}$ такие, что шарики $\mathbf {G}$ попарно не пересекаются и удовлетворяют $$\bigcup _{B\in \mathbf {F} }B\subseteq \bigcup _{C\in \mathbf {G} }5\,C.$$И более того, каждый $B\in \mathbf {F}$ пересекает некоторые $C\in \mathbf {G}$ с $B\subset 5C$.

Доказательство: рассмотрим разбиение F на поднаборы F _n , n ≥ 0, определяемые формулой

$\mathbf {F} _{n}=\{B\in \mathbf {F} :2^{-n-1}R<{\text{rad}}(B)\leq 2^{-n}R\}.$

То есть, ${\textstyle \mathbf {F} _{n}}$ состоит из шаров B, радиус которых равен (2 ^{− п −1} Р , 2 ^{− п} Р ]. Последовательность Gn _. , при которой ⊂ _Gn Fn , _{определяется} индуктивно следующим образом Сначала положим H ₀ = F ₀ и пусть G ₀ — максимальное непересекающееся подмножество H ₀ (такое подмножество существует по лемме Цорна ). Полагая, что , _G0 ..., Gn _пусть выбраны,

$\mathbf {H} _{n+1}=\{B\in \mathbf {F} _{n+1}:\ B\cap C=\emptyset ,\ \ \forall C\in \mathbf {G} _{0}\cup \mathbf {G} _{1}\cup \dots \cup \mathbf {G} _{n}\},$

и пусть G _{n +1} — максимальное непересекающееся подмножество в H _{n +1} . Подколлекция

$\mathbf {G} :=\bigcup _{n=0}^{\infty }\mathbf {G} _{n}$

множества F удовлетворяет требованиям теоремы: G — непересекающаяся совокупность и, следовательно, счетна, поскольку данное метрическое пространство сепарабельно. Более того, каждый шар B ∈ F пересекает шар C ∈ G такой, что B ⊂ 5 C .
Действительно, если нам дать некоторые $B\in \mathbf {F}$, должен существовать такой n , что B принадлежит F _n . Либо B не принадлежит H _n , что означает n > 0 и означает, что B пересекает шар из объединения G ₀ , ..., G _{n −1} , или B ∈ H _n и в силу максимальности G _n , B пересекает шар в G _n . случае B пересекает шар C принадлежащий объединению G0 _, ,..., Gn _. В любом Такой шар C должен иметь радиус больше 2 ^{− п −1} Р. ​Поскольку радиус B меньше или равен 2 ^{− п} R, на основании неравенства треугольника мы можем заключить, что B ⊂ 5 C, как и утверждается. Из этого $\bigcup _{B\in \mathbf {F} }B\subseteq \bigcup _{C\in \mathbf {G} }5\,C$ следует сразу, завершая доказательство.

Примечания

• В бесконечной версии исходный набор шаров может быть счетным или несчетным . В сепарабельном метрическом пространстве любой попарно непересекающийся набор шаров должен быть счетным. В несепарабельном пространстве тот же аргумент показывает, что существует попарно непересекающееся подсемейство, но это семейство не обязательно должно быть счетным.
• Результат может оказаться неверным, если радиусы не ограничены: рассмотрим семейство всех шаров с центром в точке 0 в R. ^д ; любое непересекающееся подсемейство состоит только из одного шара B , а 5 B не содержит всех шаров этого семейства.
• Константа 5 не является оптимальной. Если масштаб c ^{− п} , c > 1, используется вместо 2 ^{− п} для определения F _n окончательное значение равно 1 + 2 c вместо 5. Любая константа больше 3 дает правильное утверждение леммы, но не 3.
• Используя более тонкий анализ, когда исходный набор F является покрытием Витали подмножества E из R ^д , можно показать, что подколлекция G , определенная в приведенном выше доказательстве, покрывает E с точностью до множества, пренебрегаемого Лебегом.

Приложения и способ использования

Применение леммы Витали заключается в доказательстве максимального неравенства Харди – Литтлвуда . Как и в этом доказательстве, лемма Витали часто используется, например, когда мы рассматриваем d -мерную меру Лебега : $\lambda _{d}$, множества E ⊂ R ^д , который, как мы знаем, содержится в объединении некоторого набора шаров $\{B_{j}:j\in J\}$, каждый из которых имеет меру, которую нам легче вычислить, или имеет особое свойство, которое хотелось бы использовать. Следовательно, если мы вычислим меру этого объединения, мы получим верхнюю границу меры E . Однако трудно вычислить меру объединения всех этих шаров, если они перекрываются. По лемме Витали мы можем выбрать подколлекцию $\left\{B_{j}:j\in J'\right\}$ который не пересекается и такой, что ${\textstyle \bigcup _{j\in J'}5B_{j}\supset \bigcup _{j\in J}B_{j}\supset E}$. Поэтому,

$\lambda _{d}(E)\leq \lambda _{d}{\biggl (}\bigcup _{j\in J}B_{j}{\biggr )}\leq \lambda _{d}{\biggl (}\bigcup _{j\in J'}5B_{j}{\biggr )}\leq \sum _{j\in J'}\lambda _{d}(5B_{j}).$

Теперь, поскольку увеличение радиуса d -мерного шара в пять раз увеличивает его объем в 5 раз ^д , мы это знаем

$\sum _{j\in J'}\lambda _{d}(5B_{j})=5^{d}\sum _{j\in J'}\lambda _{d}(B_{j})$

и таким образом

$\lambda _{d}(E)\leq 5^{d}\sum _{j\in J'}\lambda _{d}(B_{j}).$

Теорема

В теореме о покрытии цель состоит в том, чтобы покрыть с точностью до «незначительного множества» заданное множество E ⊆ R. ^д непересекающейся подколлекцией, извлеченной из покрытия Витали для E : класс Витали или покрытие Витали ${\mathcal {V}}$ ибо E — это набор множеств такой, что для каждого x ∈ E и δ > 0 существует множество U в наборе ${\mathcal {V}}$ такой, что ∈ U и диаметр U отличен x от нуля и меньше δ .

В классической постановке Виталия пренебрежимо малое множество - это пренебрежимо малое множество Лебега , но меры, отличные от меры Лебега, и пространства, отличные от R ^д также рассматривались, как показано в соответствующем разделе ниже.

Полезно следующее наблюдение: если ${\mathcal {V}}$ является накрытием Витали для E , и если E содержится в открытом множестве Ω ⊆ R ^д , то подколлекция множеств U в ${\mathcal {V}}$ содержащиеся в Ω, также является накрытием Витали для E .

Витали о покрытии

Следующая теорема о покрытии для меры Лебега λ _d принадлежит Лебегу (1910) . Коллекция ${\mathcal {V}}$ измеримых подмножеств R ^д является регулярной семьей (в смысле Лебега ), если существует константа C такая, что

$\operatorname {diam} (V)^{d}\leq C\,\lambda _{d}(V)$

для каждого набора V в коллекции ${\mathcal {V}}$.
Семейство кубиков является примером правильного семейства. ${\mathcal {V}}$как и семья ${\mathcal {V}}(m)$ прямоугольников в R ² такое, что отношение сторон остается между m ⁻¹ и m для некоторого фиксированного m задана произвольная норма ≥ 1. Если на R ^д , еще одним примером является семейство шаров для метрики, связанной с нормой. Напротив, семейство всех прямоугольников в R ² является не регулярным.

Теорема . Пусть E ⊆ R ^д — измеримое множество с конечной мерой Лебега, и пусть ${\mathcal {V}}$ — регулярное семейство замкнутых подмножеств R ^д это прикрытие Витали для E . Тогда существует конечная или счетно бесконечная непересекающаяся подколлекция $\{U_{j}\}\subseteq {\mathcal {V}}$ такой, что $$\lambda _{d}{\biggl (}E\setminus \bigcup _{j}U_{j}{\biggr )}=0.$$

Оригинальный результат Витали (1908) представляет собой частный случай этой теоремы, в котором d = 1 и ${\mathcal {V}}$ представляет собой совокупность интервалов, являющуюся накрытием Витали измеримого подмножества E вещественной прямой, имеющей конечную меру.
Приведенная выше теорема остается верной даже без предположения, что E имеет конечную меру. Это получается путем применения результата о покрытии в случае конечной меры для каждого целого числа n ≥ 0 к части E , содержащейся в открытом кольце Ω _n точек x такой, что n < | х | < п +1.

Несколько родственная теорема о покрытии — это теорема о покрытии Безиковича . Каждой точке a подмножества A ⊆ R ^д евклидов шар B ( a , ra _и ) с центром a положительным радиусом . _ra , задан Затем, как и в лемме Витали о покрытии, выбирается поднабор этих шаров, чтобы покрыть A определенным образом. Основные различия между теоремой о накрытии Безиковича и леммой о накрытии Витали заключаются в том, что, с одной стороны, требование Витали о дизъюнктности смягчено до того факта, что число N _x выбранных шаров, содержащих произвольную точку x ∈ R ^д ограничен константой Bd _, зависящей только от размерности d ; с другой стороны, выбранные шары покрывают множество A всех данных центров.

Витали о покрытии

Аналогичная цель может возникнуть при рассмотрении меры Хаусдорфа вместо меры Лебега. В этом случае применима следующая теорема.

Теорема . Пусть H ^с обозначим s -мерную меру Хаусдорфа, пусть E ⊆ R ^д быть Н ^с - измеримое множество и ${\mathcal {V}}$ класс Виталиязамкнутых множеств для E . Тогда существует (конечный или счетный) непересекающийся поднабор. $\{U_{j}\}\subseteq {\mathcal {V}}$ такой, что либо $$H^{s}\left(E\setminus \bigcup _{j}U_{j}\right)=0$$ или $$\sum _{j}\operatorname {diam} (U_{j})^{s}=\infty .$$

Более того, если E имеет конечную s -мерную меру Хаусдорфа, то для любого ε > 0 мы можем выбрать этот поднабор { U _j } такой, что

$H^{s}(E)\leq \sum _{j}\mathrm {diam} (U_{j})^{s}+\varepsilon .$

Из этой теоремы следует приведенный выше результат Лебега. Действительно, когда s = d , мера Хаусдорфа H ^с на R ^д совпадает с кратной d -мерной мере Лебега. Если непересекающаяся коллекция $\{U_{j}\}$ регулярен и содержится в измеримой области B с конечной мерой Лебега, то

$\sum _{j}\operatorname {diam} (U_{j})^{d}\leq C\sum _{j}\lambda _{d}(U_{j})\leq C\,\lambda _{d}(B)<+\infty$

что исключает вторую возможность в первом утверждении предыдущей теоремы. Отсюда следует, что E покрывается с точностью до пренебрежимо для Лебега множества выбранным непересекающимся поднабором.

От леммы о покрытии к

Лемму о накрытии можно использовать как промежуточный шаг в доказательстве следующей основной формы теоремы о накрытии Витали.

Теорема . Для каждого подмножества E из R ^д и для каждого покрытия Витали E набором F замкнутых шаров существует непересекающийся подколледж G , который покрывает E с точностью до множества, пренебрегаемого Лебегом.

Доказательство: Без ограничения общности можно считать, что все шары в F невырождены и имеют радиус меньше или равный 1. По бесконечной форме леммы о накрытии существует счетное непересекающееся подмножество. $\mathbf {G}$ из F такой, что каждый шар B ∈ F пересекает шар C ∈ G, для которого B ⊂ 5 C . Пусть r задано > 0, и пусть Z обозначает множество точек z ∈ E , которые не содержатся ни в одном шаре из G и принадлежат открытому шару B ( r ) радиуса r с центром в 0. Достаточно показать что Z пренебрежимо мал по Лебегу для каждого заданного r .

Позволять $\mathbf {G} _{r}=\{C_{n}\}_{n}$ обозначаем поднабор тех шаров в G, которые пересекают B ( r ). Обратите внимание, что $\mathbf {G} _{r}$ может быть конечным или счетным. Пусть z ∈ Z фиксировано. Для каждого N z не принадлежит замкнутому множеству $K=\bigcup _{n\leq N}C_{n}$ определению З. по Но по свойству накрытия Витали можно найти шар B ∈ F , содержащий z содержащийся в B ( r ) и не пересекающийся с K. , По свойству G шар B пересекает некоторый шар $C_{i}\in \mathbf {G}$ и содержится в $5C_{i}$. Но поскольку K и B не пересекаются, мы должны иметь i > N. Итак, $z\in 5C_{i}$ для некоторого i > N, и поэтому

$Z\subset \bigcup _{n>N}5C_{n}.$

Это дает для каждого N неравенство

$\lambda _{d}(Z)\leq \sum _{n>N}\lambda _{d}(5C_{n})=5^{d}\sum _{n>N}\lambda _{d}(C_{n}).$

Но поскольку шары $\mathbf {G} _{r}$ содержатся в B(r+2) и эти шары не пересекаются, мы видим

$\sum _{n}\lambda _{d}(C_{n})<\infty .$

Следовательно, член в правой части приведенного выше неравенства сходится к 0, когда N стремится к бесконечности, что показывает, что Z при необходимости пренебрежимо мал.

Бесконечномерные пространства

Теорема Витали о накрытии недействительна в бесконечномерных условиях. Первый результат в этом направлении дал Дэвид Прейсс в 1979 году: существует гауссова мера γ на (бесконечномерном) сепарабельном гильбертовом пространстве H, так что теорема о накрытии Витали неверна для ( H , Borel( H ), γ ). Этот результат был усилен в 2003 году Ярославом Тишером: теорема о покрытии Витали фактически неверна для любой бесконечномерной гауссовой меры в любом (бесконечномерном) сепарабельном гильбертовом пространстве.

См. также

• Теорема о покрытии Безиковича

Ссылки

• Эванс, Лоуренс К.; Гариепи, Рональд Ф. (1992), Теория меры и тонкие свойства функций , Исследования по высшей математике, Бока-Ратон, Флорида : CRC Press , стр. viii+268, ISBN  0-8493-7157-0 , МР   1158660 , Збл   0804.28001
• Фальконер, Кеннет Дж. (1986), Геометрия фрактальных множеств , Cambridge Tracts in Mathematics, vol. 85, Кембридж: Издательство Кембриджского университета , стр. xiv+162, ISBN  0-521-25694-1 , МР   0867284 , Збл   0587.28004
• «Теорема Витали» , Математическая энциклопедия , EMS Press , 2001 [1994]
• Лебег, Анри (1910), «Об интегрировании разрывных функций» , Annales Scientifiques de l'École Normale Supérieure , 27 : 361–450, doi : 10.24033/asens.624 , JFM   41.0457.01
• Натансон, И.П. (1955), Теория функций действительной переменной , Нью-Йорк: Frederick Ungar Publishing Co. , стр. 277, МР   0067952 , Збл   0064.29102
• Прейсс, Дэвид (1979), «Гауссовы меры и теоремы покрытия», Математическое обозрение Университета Каролины , 20 (1): 95–99, ISSN   0010-2628 , MR   0526149 , Zbl   0386.28015
• Штейн, Элиас М .; Шакарчи, Рами (2005), Реальный анализ. Теория меры, интегрирование и гильбертовы пространства , Принстонские лекции по анализу, III, Принстон, Нью-Джерси : Princeton University Press, стр. xx+402, ISBN  0-691-11386-6 , МР   2129625 , Збл   1081.28001
• Тишер, Ярослав (2003), «Теорема о покрытии Витали в гильбертовом пространстве», Труды Американского математического общества , 355 (8): 3277–3289 (электронный), doi : 10.1090/S0002-9947-03-03296-3 , MR   1974687 , Збл   1042.28014
• Витали, Джузеппе (1908) [17 декабря 1907 г.], «О группах точек и функциях действительных переменных» , Atti dell'Accademia delle Scienze di Torino (на итальянском языке), 43 : 75–92, JFM   39.0101.05 (название перевод) « О группах точек и функциях действительных переменных » — статья, содержащая первое доказательство теоремы Витали о накрытии .