Теория трехфазного движения

Теория трехфазного движения — это теория транспортных потоков, разработанная Борисом Кернером в период с 1996 по 2002 год. В основном основное внимание уделяется объяснению физики нарушений дорожного движения и возникающих в результате заторов на автомагистралях. Кернер описывает три фазы дорожного движения, тогда как классические теории, основанные на фундаментальной диаграмме транспортных потоков, выделяют две фазы: свободный поток и перегруженный трафик . Теория Кернера делит перегруженное движение на две отдельные фазы: синхронизированный поток и широкая движущаяся пробка , в результате чего общее количество фаз достигает трех:

Синхронизированный поток

час

1. Свободный поток ( F )
2. Синхронизированный поток ( S )
3. Широкий движущийся затор ( J )

Слово «широкий» используется даже несмотря на то, что речь идет о длине пробки.

Фаза состояние определяется как в пространстве и времени.

Свободный поток ( F )

При свободном транспортном потоке эмпирические данные показывают положительную корреляцию между скоростью потока $q$ (в транспортных средствах в единицу времени) и плотность транспортных средств $k$ (в транспортных средствах на единицу расстояния). Эта связь прекращается при максимальном свободном потоке. $q_{\max }$ с соответствующей критической плотностью $k_{\text{crit}}$. (См. рисунок 1.)

Рисунок 1: Измеренная скорость потока в зависимости от плотности транспортного средства в свободном потоке (вымышленные данные)

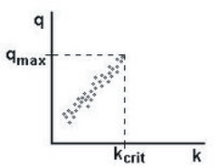
Перегруженное движение

Данные показывают более слабую связь между расходом и плотностью в условиях заторов. Поэтому Кернер утверждает, что фундаментальная диаграмма , используемая в классической теории дорожного движения, не может адекватно описать сложную динамику автомобильного движения. Вместо этого он делит заторы на синхронизированный поток и широкие движущиеся пробки .

В пробках скорость автомобиля ниже минимальной скорости автомобиля. $v_{\text{free}}^{\min }$ встречающаяся в свободном потоке, т. е. линия с наклоном минимальной скорости $v_{\text{free}}^{\min }={\frac {q_{\max }}{k_{\text{crit}}}}$ в свободном потоке (пунктирная линия на рисунке 2) делит эмпирические данные на плоскости плотности потока на две области: на левой стороне точки данных свободного потока и на правой стороне точки данных, соответствующие перегруженному трафику.

Рисунок 2. Зависимость скорости потока от плотности транспортных средств в условиях свободного потока и заторов (вымышленные данные)

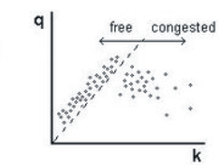
Определения [ J ] и [ S ] фаз J и S в условиях перегруженного движения.

В теории Кернера фазы J и S в перегруженном трафике являются наблюдаемыми результатами универсальных пространственно-временных характеристик реальных данных о дорожном движении . Фазы J и S определяются посредством определений [ J ] и [ S ] следующим образом:

Рисунок 3: Измеренные данные скорости во времени и пространстве (а) и их представление на плоскости время-пространство (б)

Фаза «широкого движущегося затора» [ J ]

Так называемая «широкая движущаяся пробка» движется вверх по течению через любые узкие места на шоссе . При этом средняя скорость нисходящего фронта $v_{g}$ сохраняется. Это характерная особенность широкого движущегося затора, определяющего J. фазу

Термин «широкая движущаяся пробка» призван отражать характерную особенность затора распространяться через любое другое состояние транспортного потока и через любое узкое место , сохраняя при этом скорость фронта затора ниже по течению. Фраза «движущаяся пробка» отражает распространение пробки как целостной локализованной структуры на дороге. Чтобы отличить широкие движущиеся заторы от других движущихся заторов, которые обычно не поддерживают среднюю скорость фронта нисходящего потока, Кернер использовал термин « широкие» . Термин «широкий» отражает тот факт, что если движущаяся затор имеет ширину (в продольном направлении дороги) значительно большую, чем ширина фронтов затора, и если скорость автомобиля внутри затора равна нулю, затор всегда имеет характерную особенность: поддержание скорости нисходящего фронта затора (см. раздел 7.6.5 книги ).Таким образом, термин «широкий» не имеет ничего общего с шириной затора, а на самом деле означает, что его длина значительно больше, чем переходные зоны в его голове и хвосте. Исторически Кернер использовал термин «широкий» из качественной аналогии широкой движущейся пробки в транспортном потоке с широкими автосолитонами , встречающимися во многих системах естествознания (таких как газовая плазма, электронно-дырочная плазма в полупроводниках, биологических системах и химических реакциях): широкий движущийся затор и широкий автосолитон обладают некоторыми характерными особенностями, не зависящими от начальных условий, при которых возникли эти локализованные закономерности.

Фаза «синхронизированного потока» [ S ]

В «синхронизированном потоке» на переднем фронте, где транспортные средства разгоняются до свободного потока, не проявляется эта характерная черта широкой движущейся пробки. В частности, нижний фронт синхронизированного потока часто оказывается в узком месте.

Термин «синхронизированный поток» предназначен для отражения следующих особенностей этой фазы движения: (i) Это непрерывный транспортный поток без значительных остановок, что часто происходит внутри широкой движущейся пробки. Термин «поток» отражает эту особенность. (ii) На многополосной дороге в этом потоке наблюдается тенденция к синхронизации скорости транспортных средств на разных полосах движения. Кроме того, наблюдается тенденция к синхронизации скоростей транспортных средств на каждой из полос движения (скопление транспортных средств) в синхронизированном потоке. Это связано с относительно низкой вероятностью прохождения. Термин «синхронизированный» отражает эффект синхронизации скорости.

Пояснение определений фаз трафика на основе измеренных данных о трафике

Измеренные данные усредненных скоростей транспортных средств (рисунок 3(а)) иллюстрируют определения фаз [ J ] и [ S ]. На рисунке 3 (а) представлены две пространственно-временные модели перегруженного движения с низкой скоростью движения транспортных средств. Одна волна распространяется вверх по течению с почти постоянной скоростью нисходящего фронта, двигаясь прямо через узкое место на автостраде. Согласно определению [ J ], такая модель заторов относится к фазе «широкой движущейся пробки». Напротив, нижний фронт другой модели зафиксирован на узком месте. По определению [ S ] данная закономерность относится к фазе «синхронизированного течения» (рис. 3 (а) и (б)). Другие эмпирические примеры проверки определений фаз дорожного движения [ J ] и [ S ] можно найти в книгах. и, в статье а также в эмпирическом исследовании данных о плавающих автомобилях (Плавающие данные автомобиля также называются данными зонда автомобиля ).

Определение фазы движения на основе эмпирических данных по одному транспортному средству

В гл. 6.1 книги Было показано, что определения фаз дорожного движения [ S ] и [ J ] являются источником большинства гипотез трехфазной теории и связанных с ней трехфазных микроскопических моделей транспортных потоков. Определения фазы трафика [ J ] и [ S ] являются нелокальными макроскопическими определениями и применимы только после того, как макроскопические данные были измерены в пространстве и времени, т. е. в «автономном» исследовании. Это связано с тем, что для окончательного разграничения фаз J и S посредством определений [ J ] и [ S ] необходимо исследование распространения пробок на дорогах через узкое место. Это часто рассматривается как недостаток определений фазы трафика [ S ] и [ J ]. Однако существуют локальные микроскопические критерии различия фаз J и S без изучения распространения перегруженного трафика через узкое место. Микроскопические критерии таковы (см. раздел 2.6 в книге ): Если в данных по одному транспортному средству ( микроскопических ), связанных с перегруженным движением, наблюдается «интервал прерывания потока», т. е. временной интервал между двумя транспортными средствами, следующими друг за другом, который намного превышает среднее время задержки ускорения транспортного средства от широкого движущегося затора (последнее составляет около 1,3–2,1 с), то соответствующий интервал прерывания потока соответствует фазе широкого движущегося затора. После того, как по этому критерию в условиях перегруженного движения были обнаружены все широкие движущиеся пробки, все оставшиеся состояния перегруженности относятся к фазе синхронизированного потока.

Гипотеза Кернера о двумерных (2D) состояниях транспортного потока.

Устойчивые состояния синхронизированного потока

Однородный синхронизированный поток — это гипотетическое состояние синхронизированного потока идентичных транспортных средств и водителей, при котором все транспортные средства движутся с одинаковой независимой от времени скоростью и имеют одинаковые пространственные промежутки (пространственный разрыв — это расстояние между одним транспортным средством и тем, что следует за ним). т. е. этот синхронизированный поток однороден во времени и пространстве.

Гипотеза Кернера состоит в том, что однородный синхронизированный поток может возникать в любом месте двумерной области (2D) плоскости плотности потока (2D-область S на рисунке 4 (а)). Набор возможных состояний свободного потока (F) по плотности транспортных средств перекрывается с набором возможных состояний однородного синхронизированного потока. Состояния свободного потока на многополосной дороге и состояния однородного синхронизированного потока разделены разрывом в скорости потока и, следовательно, разрывом в скорости при данной плотности: при каждой данной плотности скорость синхронизированного потока меньше чем скорость свободного потока.

В соответствии с этой гипотезой трехфазной теории Кернера, при заданной скорости в синхронизированном потоке водитель может сделать произвольный выбор расстояния до предыдущего транспортного средства в пределах диапазона, связанного с двумерной областью однородного синхронизированного потока ( Рисунок 4(b)): драйвер принимает разные пробелы в разное время и не использует один уникальный пробел.

Рисунок 4: Гипотеза теории трехфазного движения Кернера о 2D-области установившихся состояний синхронизированного потока в плоскости поток-плотность: (a) Качественное представление состояний свободного потока (F) и 2D-области однородного синхронизированного потока (пунктирная область S) ) на многополосной дороге в плоскости плотности потока. (б) Часть 2D-области однородного синхронного течения в плоскости скорости зазора (штриховая область S). В (б) $G$ и $g_{\text{safe}}$, являются соответственно зазором в пространстве синхронизации и зазором в безопасном пространстве между двумя транспортными средствами, следующими друг за другом.

Гипотеза трехфазной теории дорожного движения Кернера о двумерной области установившихся состояний синхронизированного потока противоречит гипотезе более ранних теорий транспортных потоков, включающих фундаментальную диаграмму транспортных потоков , которая предполагает одномерную связь между плотностью транспортных средств и скоростью потока. .

Следование за автомобилем в теории трехфазного движения

В трехфазной теории Кернера транспортное средство ускоряется, когда космический зазор $g$ до предыдущего автомобиля больше, чем зазор в пространстве синхронизации $G$, то есть в $g>G$ (обозначено ускорением на рисунке 5); Транспортное средство замедляется, когда зазор g меньше безопасного зазора $g_{\text{safe}}$, то есть в $g<g_{\rm {safe}}$ (обозначено замедлением на рисунке 5).

Рисунок 5. Качественное объяснение следования за автомобилем в теории трехфазного движения Кернера: транспортное средство ускоряется в пространстве. $g>G$ и тормозит на космических разрывах $g<g_{\text{safe}}$, тогда как при условии $g_{\text{safe}}\leq g\leq G$ Транспортное средство адаптирует свою скорость к скорости предшествующего транспортного средства, не заботясь о точном расстоянии. Пунктирная область синхронизированного потока взята из рисунка 4 (б).

Если зазор меньше G , водитель стремится адаптировать свою скорость к скорости идущего впереди транспортного средства, не заботясь о том, каков точный зазор, при условии, что этот зазор не меньше безопасного пространства. $g_{\text{safe}}$ (обозначено адаптацией скорости на рисунке 5). Таким образом, космический разрыв $g$ в автомобиле следующим в рамках трехфазной теории Кернера может быть любой зазор в пределах диапазона зазора $g_{\text{safe}}\leq g\leq G$.

Автономное вождение в рамках теории трехфазного движения

В рамках трехфазной теории гипотеза о двумерных областях состояний синхронизированного потока также была применена для разработки модели автономного вождения (также называемого автоматическим вождением , беспилотным или автономным транспортным средством).

Распад трафика – F → S фазовый переход

Согласно измеренным данным, перегруженное движение чаще всего возникает вблизи узких мест на автомагистралях, например, въездов, съездов или дорожных работ. Переход от свободного потока к перегруженному трафику известен как разбивка трафика. В теории трехфазного трафика Кернера разбивка трафика объясняется фазовым переходом от свободного потока к синхронизированному потоку (так называемому фазовому переходу F → S). Это объяснение подтверждается имеющимися измерениями, поскольку в измеренных данных о трафике после сбоя трафика в узком месте нисходящий фронт перегруженного трафика фиксируется в узком месте. Следовательно, результирующий перегруженный трафик после сбоя трафика удовлетворяет определению [ S ] фазы «синхронизированного потока».

Эмпирические спонтанные и индуцированные F → S переходы

Кернер, используя эмпирические данные, отмечает, что синхронизированный поток может формироваться в свободном потоке самопроизвольно (спонтанный фазовый переход F → S) или может быть индуцирован извне (индуцированный фазовый переход F → S).

Спонтанный фазовый переход F → S означает, что пробой происходит, когда ранее в узком месте, а также вверх и вниз по потоку существовал свободный поток. Это означает, что спонтанный фазовый переход F → S происходит за счет роста внутреннего возмущения свободного потока в окрестности узкого места.

Напротив, индуцированный фазовый переход F → S происходит через область перегруженного движения, которая первоначально возникла в другом месте дороги ниже по течению от места узкого места. Обычно это связано с распространением вверх по потоку синхронизированной области течения или широким движущимся затором. Эмпирический пример вызванного пробоя в узком месте, ведущего к синхронному потоку, можно увидеть на рисунке 3: синхронизированный поток возникает в результате распространения вверх по течению широкого движущегося затора.Существование эмпирически вызванного сбоя движения (т. е. эмпирически вызванного фазового перехода F → S) означает, что фазовый переход F → S происходит в метастабильном состоянии свободного потока на узком месте шоссе. Термин «метастабильный свободный поток» означает, что когда в свободном потоке происходят небольшие возмущения, состояние свободного потока все еще стабильно, т. е. свободный поток сохраняется в узком месте. Однако когда в свободном потоке вблизи узкого места возникают более крупные возмущения, свободный поток становится нестабильным, и в узком месте возникает синхронизированный поток.

Физическое объяснение распада трафика в трехфазной теории

Рисунок 6: Объяснение разбивки трафика с помощью Z-подобной нелинейной прерывистой функции вероятности обгона в теории трехфазного движения Кернера. Пунктирная кривая иллюстрирует критическую вероятность обгона в зависимости от плотности движения.

Кернер объясняет природу фазовых переходов F → S как соревнование между «скоростной адаптацией» и «чрезмерным ускорением». Адаптация скорости определяется как замедление транспортного средства до скорости более медленно движущегося впереди транспортного средства. Чрезмерное ускорение определяется как ускорение транспортного средства, происходящее даже в том случае, если предшествующее транспортное средство не движется быстрее, чем предшествующее транспортное средство, а предшествующее транспортное средство дополнительно не ускоряется. В теории Кернера вероятность превышения ускорения является разрывной функцией скорости транспортного средства: при одинаковой плотности транспортного средства вероятность превышения ускорения в свободном потоке больше, чем в синхронизированном потоке. Когда в пределах локального возмущения скорости адаптация скорости сильнее, чем чрезмерное ускорение, происходит фазовый переход F → S. В противном случае, когда чрезмерное ускорение превышает адаптацию скорости, начальное возмущение со временем затухает. В области синхронизированного потока сильное чрезмерное ускорение отвечает за обратный переход от синхронизированного потока к свободному потоку (переход S → F).

Механизмов превышения ускорения автомобиля может быть несколько. Можно предположить, что на многополосной дороге наиболее вероятным механизмом превышения скорости является перестроение на более быструю полосу движения. В этом случае фазовые переходы F → S объясняются взаимодействием ускорения при обгоне более медленного автомобиля (переускорение) и торможения до скорости идущего впереди более медленного автомобиля (скоростная адаптация). Обгон способствует поддержанию свободного потока. «Адаптация скорости», с другой стороны, приводит к синхронизации потока. Адаптация скорости произойдет, если обгон невозможен. Кернер утверждает, что вероятность обгона является прерывистой функцией плотности транспортных средств (рис. 6): при заданной плотности транспортных средств вероятность обгона в свободном потоке значительно выше, чем в синхронизированном потоке.

Обсуждение объяснения Кернера разбивки дорожного движения

Объяснение Кернером сбоя движения на узком месте автомагистрали фазовым переходом F → S в метастабильном свободном потоке связано со следующими фундаментальными эмпирическими особенностями сбоя движения на узком месте, обнаруженными в реальных измеренных данных: (i) Спонтанный сбой движения в начальный период свободный поток в узком месте приводит к возникновению перегруженного трафика, нисходящий фронт которого зафиксирован в узком месте (по крайней мере, в течение некоторого интервала времени), т. е. этот перегруженный трафик удовлетворяет определению [ S ] для фазы синхронизированного потока. Другими словами, спонтанный срыв трафика – это всегда фазовый переход F → S. (ii) Вероятность такого спонтанного нарушения движения является возрастающей функцией скорости потока в узком месте. (iii) При одном и том же узком месте срыв трафика может быть как спонтанным, так и вынужденным (эмпирические примеры этих фундаментальных особенностей срыва трафика см. в разделах 2.2.3 и 3.1 книги). ); по этой причине фазовый переход F → S происходит в метастабильном свободном потоке в узком месте магистрали. Как объяснялось выше, смысл термина «метастабильный свободный поток» заключается в следующем. Достаточно малые возмущения в распаде метастабильного свободного потока. Однако когда в узком месте возникает достаточно большое возмущение, фазовый переход F → S все же происходит. Такое возмущение, инициирующее фазовый переход F → S в метастабильном свободном потоке в узком месте, можно назвать ядром сбоя движения. Другими словами, реальный пробой дорожного движения (фазовый переход F → S) на узком месте автомагистрали имеет нуклеационную природу. Кернер считает эмпирическую природу возникновения нарушения дорожного движения (фазовый переход F → S) на узком месте дороги эмпирической основой дорожной и транспортной науки.

Причина теории Кернера и его критика классических теорий транспортных потоков.

Эмпирический характер возникновения нарушений движения на узких местах автомагистралей не может быть объяснен с помощью классических теорий и моделей дорожного движения. Поиск объяснения эмпирической природы зарождения сбоя движения (фазовый переход F → S) на узком месте автомагистрали стал мотивацией для разработки трехфазной теории Кернера.

В частности, в двухфазных моделях транспортных потоков, в которых разрушение транспортного потока связано с неустойчивостью свободного потока, эта неустойчивость модели приводит к фазовому переходу F → J, т.е. в этих моделях транспортного потока разрушение транспортного потока определяется спонтанным возникновением широкой движущейся затор(ы) в первоначальном свободном потоке (см. критику Кернера таких двухфазных моделей, а также других классических моделей и теорий транспортных потоков в главе 10 книги). а также в критических обзорах, ).

Основное предсказание трехфазной теории Кернера

Кернер разработал трехфазную теорию как объяснение эмпирической природы нарушения движения на узких местах шоссе: случайный (вероятностный) фазовый переход F → S, который происходит в метастабильном состоянии свободного потока.При этом Кернер объяснил основное предсказание о том, что эта метастабильность свободного течения по отношению к фазовому переходу F → S обусловлена ​​зародышевой природой неустойчивости синхронизированного течения. Объяснение заключается в достаточно большом локальном увеличении скорости синхронного потока (называемом нестабильностью S → F), которое представляет собой растущую волну скорости локального увеличения скорости синхронного потока в узком месте. Развитие неустойчивости S → F приводит к локальному фазовому переходу от синхронного течения к свободному течению в узком месте (переход S → F). Для объяснения этого явления Кернер разработал микроскопическую теорию S → F-неустойчивости. Ни одна из классических теорий и моделей транспортных потоков не учитывает нестабильность S → F трехфазной теории.

Первоначально разработанная для шоссейного движения, Кернер расширил трехфазную теорию для описания городского движения в 2011–2014 годах.

Диапазон пропускной способности шоссе

В теории трехфазного движения распад трафика объясняется переходом F → S, происходящим в метастабильном свободном потоке. Вероятно, самым важным следствием этого является существование диапазона пропускной способности автомагистралей между максимальной и минимальной пропускной способностью.

Максимальная и минимальная пропускная способность шоссе

Спонтанный пробой движения, т. е. самопроизвольный фазовый переход F → S, может произойти в широком диапазоне скоростей потока в свободном потоке. Кернер утверждает, основываясь на эмпирических данных, что из-за возможности спонтанных или вынужденных перерывов в движении на одном и том же узком месте автострады в любой момент времени существует диапазон пропускной способности шоссе в узком месте. Этот диапазон пропускной способности автомагистралей находится между минимальной пропускной способностью $C_{\min }$ и максимальная мощность $C_{\max }$ свободного потока (рис. 7).

Рисунок 7: Максимальная и минимальная пропускная способность шоссе в теории трехфазного движения Кернера.

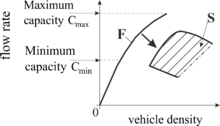
Пропускные способности магистралей и метастабильность свободного потока

Существует максимальная пропускная способность шоссе. $C_{\max }$: Если расход близок к максимальной производительности $C_{\max }$, то даже небольшие возмущения свободного потока в узком месте приведут к спонтанному фазовому переходу F → S. С другой стороны, только очень большие возмущения свободного потока в узком месте приведут к спонтанному фазовому переходу F → S, если расход близок к минимальной производительности. $C_{\min }$ (см., например, разд. 17.2.2 книги ). Вероятность меньшего возмущения свободного потока значительно выше, чем вероятность большего возмущения. Следовательно, чем выше скорость потока в свободном потоке в узком месте, тем выше вероятность спонтанного фазового перехода F → S. Если расход в свободном потоке ниже минимальной производительности $C_{\min }$, в узком месте не будет сбоя трафика (нет фазового перехода F →S).

Бесконечное количество пропускных способностей автомагистралей в узких местах можно проиллюстрировать метастабильностью свободного потока при скорости потока. $q$ с

$C_{\min }\leq q<C_{\max }.$

Метастабильность свободного течения означает, что при малых возмущениях свободный поток остается стабильным (свободное течение сохраняется), но при более крупных возмущениях течение становится неустойчивым и происходит фазовый переход F → S в синхронизированное течение.

Обсуждение определений мощности

Таким образом, основной теоретический результат трехфазной теории о понимании стохастической способности свободного потока в узком месте заключается в следующем: В любой момент времени в узком месте имеется бесконечное количество магистралей со свободным потоком. Бесконечное количество скоростей потока, при которых может возникнуть нарушение движения на узких местах, и бесконечное количество пропускных способностей автомагистралей. Эти мощности находятся в диапазоне расхода между минимальной и максимальной производительностью (рис. 7).

Диапазон пропускной способности автомагистралей, являющийся узким местом в теории трехфазного движения Кернера, в корне противоречит классическому пониманию стохастической пропускной способности автомагистралей, а также теориям дорожного движения и методам управления и контроля дорожного движения, которые в любой момент предполагают существование определенной пропускной способности автомагистралей. Напротив, в теории трехфазного движения Кернера в любой момент времени существует диапазон пропускной способности шоссе, который находится между минимальной пропускной способностью и $C_{\min }$ и максимальная мощность $C_{\max }$. Ценности $C_{\min }$ и $C_{\max }$ может существенно зависеть от параметров движения (доля длинномерных транспортных средств в транспортном потоке, погода, характеристики узких мест и т. д.).

Существование в любой момент времени диапазона пропускной способности шоссе в теории Кернера кардинально меняет методологии управления дорожным движением, динамического распределения трафика и управления дорожным движением. В частности, чтобы удовлетворить природу возникновения аварийных ситуаций, Кернер ввел принцип минимизации аварийных ситуаций (принцип BM) для оптимизации и управления сетями автомобильного движения.

Широкие движущиеся пробки ( J )

Движущаяся затор будет называться «широким», если его длина (по направлению потока) явно превышает длины фронтов затора. Средняя скорость автомобиля в широких движущихся пробках значительно ниже средней скорости в свободном потоке. На заднем фронте автомобили разгоняются до скорости свободного потока. На фронте затора выше по течению транспортные средства приходят из свободного или синхронного потока и должны снизить скорость. Согласно определению [ J ] широкий движущийся затор всегда имеет ту же среднюю скорость, что и встречный фронт. $v_{g}$, даже если затор распространяется на другие этапы трафика или узкие места. Скорость потока резко снижается в пределах широкого движущегося затора.

Характерные параметры широких движущихся пробок

Эмпирические результаты Кернера показывают, что некоторые характерные особенности широких движущихся пробок не зависят от интенсивности движения и особенностей узких мест (например, где и когда образовалась пробка). Однако эти характерные особенности зависят от погодных условий, дорожных условий, технологии транспортного средства, процента длинномерных транспортных средств и т. д. Скорость нисходящего фронта широкой движущейся пробки $v_{g}$ (в восходящем направлении) является характеристическим параметром, как и скорость потока сразу за затором. $q_{\text{out}}$ (при свободном потоке в этом месте, см. рисунок 8). Это означает, что многие широко движущиеся заторы имеют схожие характеристики в аналогичных условиях. Эти параметры относительно предсказуемы. Движение нижнего фронта затора можно проиллюстрировать в плоскости плотности потока линией, которая называется «Линия J» (Линия J на ​​рисунке 8). Наклон линии J представляет собой скорость нисходящего фронта затора. $v_{g}$.

Рисунок 8: Три фазы трафика на плоскости плотности потока в теории трехфазного трафика Кернера.

Минимальная пропускная способность магистрали и отток из-за широкой движущейся пробки

Кернер подчеркивает, что минимальная мощность $C_{\min }$ и истечение широкой движущейся пробки $q_{\text{out}}$ описывают две качественно разные характеристики свободного потока: минимальную производительность $C_{\min }$ характеризует фазовый переход F → S в узком месте, т. е. обрыв трафика. Напротив, истечение широкой движущейся пробки $q_{\text{out}}$ определяет условие существования широкого движущегося затора, т. е. фазу движения J при свободном распространении затора: Действительно, если затор распространяется в свободном потоке (т. е. как вверх, так и после затора возникают свободные течения) , то широкая подвижная затор может сохраняться, только когда затор притекает $q_{\text{in}}$ равен или больше, чем выход затора $q_{\text{out}}$; в противном случае варенье со временем растворится. В зависимости от параметров дорожного движения, таких как погода, процент длинномерных транспортных средств и т. д., а также характеристик узкого места, где может произойти фазовый переход F → S, минимальная пропускная способность $C_{\min }$ может быть меньше (как на рисунке 8) или больше, чем выход затора. $q_{\text{out}}$.

Синхронизированная фаза потока ( S )

В отличие от широких движущихся пробок, на синхронизированной фазе потока как скорость потока, так и скорость транспортного средства могут существенно различаться. Нижний фронт синхронизированного потока часто пространственно фиксирован (см. определение [ S ]), обычно в узком месте в определенном месте дороги. Скорость потока на этом этапе может оставаться такой же, как и в свободном потоке, даже если скорость транспортного средства резко снижается.

Поскольку фаза синхронизированного потока не имеет характерных особенностей фазы широкого движущегося затора J , теория трехфазного движения Кернера предполагает, что гипотетические однородные состояния синхронизированного потока охватывают двумерную область в плоскости плотности потока (пунктирные области на графике). Рисунок 8).

S → J Фазовый переход

Широкие движущиеся пробки не возникают самопроизвольно в свободном потоке, но могут возникать в областях синхронизированного потока. Этот фазовый переход называется фазовым переходом S → J.

«Застревание без видимой причины» – фазовые переходы F → S → J.

Рисунок 9: Эмпирический пример каскада фазовых переходов F → S → J в теории трехфазного движения Кернера: (а) Фазовые переходы, происходящие в пространстве и времени. (б) Представление тех же фазовых переходов, что и в (а), в плоскости скорость-плотность (стрелки S → F, J → S и J → F показывают возможные фазовые переходы).

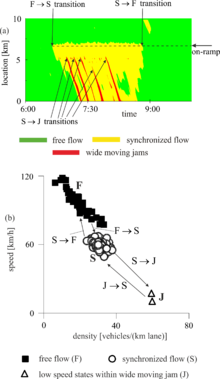
В 1998 году Кернер обнаружил, что в реальных данных о дорожном движении появление широкой движущейся пробки в свободном потоке наблюдается как каскад фазовых переходов F → S → J (рис. 9): сначала в области свободного потока возникает область синхронизированного потока. поток. Как объяснялось выше, такой фазовый переход F → S происходит в основном в узком месте. В рамках фазы синхронизированного потока происходит дальнейшее «самосжатие», плотность транспортного средства увеличивается, а скорость транспортного средства снижается. Это самосжатие называется «пинч-эффектом». В «защемленных» областях синхронного течения возникают узкие движущиеся пробки. Если эти узкие движущиеся заторы будут расти, появятся широкие движущиеся заторы, отмеченные буквами S → J на ​​рисунке 9). Таким образом, широкие движущиеся пробки возникают позже, чем произошел сбой движения (переход F → S), и на другом участке дороги выше по течению от узкого места. Поэтому, когда фазовые переходы Кернера F → S → J, происходящие в реальном дорожном движении (рис. 9 (а)) представлены в плоскости скорость-плотность (рис. 9 (б)) (или плоскости скорость-поток, или еще поток-плотность) Следует помнить, что состояния синхронного потока и состояния низкой скорости в пределах широкой движущейся пробки измеряются в разных местах дороги. Кернер отмечает, что частота возникновения широких движущихся пробок увеличивается, если увеличивается плотность в синхронном потоке. Широкие движущиеся пробки распространяются дальше вверх по течению, даже если они распространяются через области синхронизированного потока или узкие места. Очевидно, что возможна и любая комбинация обратных фазовых переходов (переходы S → F, J → S и J → F, показанные на рисунке 9).

Физика S → J перехода

Чтобы дополнительно проиллюстрировать фазовые переходы S → J: в теории трехфазного движения Кернера линия J делит однородные состояния синхронизированного потока на две части (рис. 8). Состояния однородного синхронизированного потока выше линии J метастабильны. Состояния однородного синхронизированного течения ниже линии J являются устойчивыми состояниями, в которых не может произойти фазовый переход S → J. Метастабильный однородный синхронизированный поток означает, что при небольших возмущениях состояние дорожного движения остается стабильным. Однако при возникновении более крупных возмущений синхронизированное течение становится неустойчивым и происходит фазовый переход S → J.

Схема движения S и J

Могут наблюдаться очень сложные закономерности перегрузки, вызванные фазовыми переходами F → ​​S и S → J.

Классификация шаблонов трафика синхронизированных потоков (SP)

Схема перегрузки синхронизированного потока (синхронизированная структура потока (SP)) с фиксированным нисходящим фронтом и непостоянно распространяющимся восходящим фронтом называется локализованной синхронизированной структурой потока (LSP).

Часто восходящий фронт СП распространяется вверх по течению. Если вверх по течению распространяется только восходящий фронт, соответствующий SP называется расширением синхронизированной структуры потока (WSP). Нисходящий фронт остается в месте узкого места, а ширина ПП увеличивается.

Возможно, что как восходящий, так и нисходящий фронт распространяется вверх по течению. Нижний фронт больше не находится в узком месте. Этот шаблон получил название «Схема движущегося синхронизированного потока» (MSP).

Уловите эффект синхронизированного потока на узком месте на автомагистрали.

Разница между SP и широким движущимся затором становится видимой в том, что когда WSP или MSP достигают узкого места в верхнем течении, может возникнуть так называемый «эффект улова». SP окажется в узком месте, и в результате возникнет новый перегруженный шаблон. Широко движущийся затор не застревает в узком месте и движется дальше вверх по течению. В отличие от широких движущихся пробок синхронизированный поток, даже если он движется как МСП, не имеет характерных параметров. Например, скорость нисходящего фронта MSP может значительно различаться и быть разной для разных MSP. Эти особенности СП и широкие подвижные заторы являются следствием фазыопределения [S] и [J].

Общая схема перегруженного трафика (GP)

Часто встречающаяся модель перегрузки — это модель, которая содержит обе фазы перегрузки: [S] и [J]. Такой шаблон с [S] и [J] называется общим шаблоном (GP). Эмпирический пример ГП показан на рисунке 9 (а).

Рисунок 10: Измеренный ЭГП в трех узких местах $B_{1}$, $B_{2}$, и $B_{3}$

Во многих инфраструктурах автомагистралей узкие места расположены очень близко друг к другу. Схема перегрузки, синхронизированный поток которой охватывает два или более узких места, называется расширенной схемой (EP). EP может содержать только синхронизированный поток (так называемый ESP: расширенная схема синхронизированного потока)), но обычно в синхронизированном потоке образуются широкие движущиеся пробки. В таких случаях EP называется EGP (расширенный общий шаблон) (см. рисунок 10).

Применение теории трехфазного движения в транспортной технике

Рисунок 11. Структура трафика в приложении ASDA/FOTO в трех странах.

из применений теории трехфазного движения Кернера являются методы /FOTO Automatische Stau Одним Dynamic ( Analyse и ASDA широких движущихся пробок) транспортных объектов ) ( отслеживание Прогнозирование Автоматическое . ASDA/FOTO — это программный инструмент, способный быстро и эффективно обрабатывать большие объемы данных о дорожном движении на сетях автомагистралей (см. примеры трех стран, рисунок 11). ASDA/FOTO работает в онлайн-системе управления дорожным движением, основанной на измеренных данных о дорожном движении. Распознавание, отслеживание и прогнозирование [S] и [J] выполняются с использованием особенностей теории трехфазного трафика Кернера.

Дальнейшие применения теории можно увидеть в разработке моделей моделирования дорожного движения, системы измерения скорости движения (ANCONA), коллективного управления дорожным движением, помощи при движении, автономного вождения и определения состояния дорожного движения, как описано в книгах Кернера.

Математические модели транспортных потоков в рамках теории трехфазного движения Кернера

собой не математическую модель транспортного потока Трехфазная теория Кернера представляет , а качественную теорию транспортного потока, состоящую из нескольких гипотез. Гипотезы трехфазной теории Кернера должны качественно объяснить пространственно-временные явления дорожного движения в транспортных сетях, обнаруженные в реальных данных о дорожном движении, которые измерялись в течение многих лет на различных автомагистралях в разных странах. Некоторые гипотезы теории Кернера были рассмотрены выше. множество различных математических моделей Можно ожидать, что в рамках трехфазной теории Кернера можно разработать транспортных потоков.

Первой математической моделью транспортного потока в рамках трехфазной теории Кернера, которую математическое моделирование может показать и объяснить нарушение дорожного движения в результате фазового перехода F → S в метастабильном свободном потоке в узком месте, была модель Кернера-Кленова, представленная в 2002 году. Модель Кернера-Кленова представляет собой микроскопическую стохастическую модель в рамках теории трехфазного движения Кернера. В модели Кернера-Кленова транспортные средства движутся в соответствии со стохастическими правилами движения транспортных средств, которые могут быть выбраны индивидуально для каждого из транспортных средств. Несколько месяцев спустя Кернер, Кленов и Вольф разработали модель транспортного потока клеточного автомата (CA) в рамках трехфазной теории Кернера.

Стохастическая трехфазная модель транспортного потока Кернера-Кленова в рамках теории Кернера получила дальнейшее развитие для различных приложений. В частности, для моделирования въездного учета, контроля ограничения скорости, динамического распределения трафика в дорожно-транспортных сетях, движения на тяжелых и движущихся узких местах, особенностей неоднородного транспортного потока, состоящего из разных транспортных средств и водителей, методов предупреждения пробок, транспортных средств связь между транспортными средствами (V2V) для совместного вождения, поведение беспилотных автомобилей в смешанном транспортном потоке, разбивка трафика по сигналам в городском потоке, перенасыщенный городской трафик, расход топлива транспортных средств в дорожных сетях (см. 1.7 обзора ).

Со временем несколько научных групп разработали новые математические модели в рамках трехфазной теории Кернера. В частности, новые математические модели в рамках трехфазной теории Кернера были представлены в работах Цзяна, Ву, Гао и др. Дэвис, Ли, Барлович, Шокенберг и Ким (другие ссылки на математические модели в рамках теории трехфазного движения Кернера и результаты их исследований см. в разделе 1.7 обзора). ).

Критика теории

Теория подверглась критике по двум основным причинам. Во-первых, теория почти полностью основана на измерениях на Бундесавтобане 5 в Германии. Возможно, эта дорога имеет такой рисунок, но другие дороги в других странах имеют другие характеристики. Будущие исследования должны показать обоснованность теории на других дорогах в других странах мира. Во-вторых, неясно, как были интерполированы данные . Кернер использует измерения с фиксированной точкой ( петлевые детекторы ), но свои выводы делает на траекториях транспортных средств , которые охватывают всю длину исследуемой дороги. Эти траектории можно измерить напрямую только в том случае, если используются данные плавающего автомобиля , но, как уже говорилось, используются только измерения петлевого детектора. Как данные между ними были собраны или интерполированы, неясно.

На приведенную выше критику был дан ответ в недавнем исследовании данных, измеренных в США и Великобритании, которое подтверждает выводы, сделанные на основе измерений на Bundesautobahn 5 в Германии. Более того, недавно была проведена проверка теории, основанной на данных о плавающих автомобилях. В этой статье также можно найти методы пространственно-временной интерполяции данных, измеренных дорожными детекторами (см. приложения к статье).

Были высказаны и другие критические замечания, например, что понятие фаз не было четко определено и что так называемые двухфазные модели также успешно моделируют основные особенности, описанные Кернером.

На эту критику был дан ответ в обзоре. следующее. Важнейшей особенностью теории Кернера является объяснение эмпирической природы зарождения срыва движения на узком месте дороги переходом F → S. Эмпирическую природу разбивки дорожного движения нельзя объяснить с помощью более ранних теорий транспортных потоков, включая изученные двухфазные модели транспортных потоков.

См. также

• Активное управление трафиком
• Фундаментальная диаграмма
• Интеллектуальная транспортная система
• Микроскопическая модель транспортного потока
• Узкое место в трафике
• Транспортный поток
• Модель трафика
• Волна трафика
• Пробки на дорогах
• Пробки на дорогах: реконструкция с помощью трехфазной теории Кернера
• Принцип минимизации пробоя Кернера.
• Прогнозирование перевозок
• Двухжидкостная модель

Ссылки

• Лью, Генри (2005). «Физика дорожного движения: эмпирические особенности схемы автомагистралей, инженерные приложения и теория». Физика сегодня . 58 (11): 54–56. Бибкод : 2005ФТ....58к..54К . дои : 10.1063/1.2155762 .
• Гао, Кун; Цзян, Руй; Ху, Шоу-Синь; Ван, Бин-Хонг; Ву, Цин-Сун (2007). «Модель клеточного автомата с адаптацией скорости в рамках теории трехфазного движения Кернера». Физический обзор E . 76 (2): 026105. Бибкод : 2007PhRvE..76b6105G . дои : 10.1103/PhysRevE.76.026105 . ПМИД   17930102 .
• Шёнхоф, Мартин; Хелбинг, Дирк (2009). «Критика теории трехфазного движения» (PDF) . Транспортные исследования. Часть B: Методологические . 43 (7): 784. CiteSeerX   10.1.1.475.3565 . дои : 10.1016/j.trb.2009.02.004 .
• Х. Реборн, С. Кленов, «Прогнозирование трафика в условиях перегруженности», В: Р. Мейерс (ред.): Энциклопедия сложности и системных наук, Springer New York, 2009.
• Х. Реборн, Дж. Палмер, «Использование ASDA и FOTO для генерации сообщений о трафике RDS/TMC», Traffic Engineering and Control, июль 2008 г., стр. 261–266.
• Дэвис, Л. Крейг (2010). «Введение в современную теорию и управление транспортными потоками: долгий путь к теории трехфазного дорожного движения» . Физика сегодня . 63 (3): 53. Бибкод : 2010ФТ....63с..53К . дои : 10.1063/1.3366241 .
• Трейбер, Мартин; Кестинг, Арне; Хелбинг, Дирк (2010). «Теория трехфазного движения и двухфазные модели с фундаментальной схемой в свете эмпирических стилизованных фактов» . Транспортные исследования. Часть B: Методологические . 44 (8–9): 983. arXiv : 1004.5545 . Бибкод : 2010arXiv1004.5545T . CiteSeerX   10.1.1.186.2970 . дои : 10.1016/j.trb.2010.03.004 . S2CID   18335270 .
• Хартенштейн, Ханнес (2010). «Теория транспортных потоков: три, а не две фазы [обзор книги «Введение в современную теорию и управление транспортными потоками: долгий путь к теории трехфазного дорожного движения»; Кернер, бакалавр наук; 2009)]". Журнал IEEE Vehical Technology Magazine . 5 (3): 91. doi : 10.1109/MVT.2010.937837 . S2CID   21113397 .