Решение для спутниковой навигации

Решение спутниковой навигации для определения местоположения приемника ( геопозиционирование ) включает в себя алгоритм. По сути, приемник GNSS измеряет время передачи сигналов GNSS, излучаемых четырьмя или более спутниками GNSS (определяя псевдодальность ), и эти измерения используются для получения его положения (т. е. пространственных координат ) и времени приема.

Нижеследующее выражено в координатах инерциальной системы отсчета .

Решение проиллюстрировано

• 
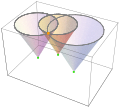
  По сути, решение, показанное оранжевым цветом, $\scriptstyle ({\hat {\boldsymbol {r}}}_{\text{rec}},\,{\hat {t}}_{\text{rec}})$, – пересечение световых конусов .
• 
  Апостериорное распределение решения получается из произведения распределения распространяющихся сферических поверхностей. (Смотрите анимацию .)

Этапы расчета

1. Приемник глобальной навигационной спутниковой системы (GNSS) измеряет кажущееся время передачи, $\displaystyle {\tilde {t}}_{i}$или «фаза» сигналов GNSS, излучаемых четырьмя или более спутниками GNSS ( $\displaystyle i\;=\;1,\,2,\,3,\,4,\,..,\,n$ ), одновременно.
2. спутников Спутники GNSS передают сообщения эфемерид , $\displaystyle {\boldsymbol {r}}_{i}(t)$и внутреннее смещение часов (т. е. опережение часов), $\displaystyle \delta t_{{\text{clock,sv}},i}(t)$ как функции ( атомного ) стандартного времени , например GPST .
3. Время передачи спутниковых сигналов ГНСС, $\displaystyle t_{i}$, таким образом, получается из незамкнутой формы уравнений $\displaystyle {\tilde {t}}_{i}\;=\;t_{i}\,+\,\delta t_{{\text{clock}},i}(t_{i})$ и $\displaystyle \delta t_{{\text{clock}},i}(t_{i})\;=\;\delta t_{{\text{clock,sv}},i}(t_{i})\,+\,\delta t_{{\text{orbit-relativ}},\,i}({\boldsymbol {r}}_{i},\,{\dot {\boldsymbol {r}}}_{i})$, где $\displaystyle \delta t_{{\text{orbit-relativ}},i}({\boldsymbol {r}}_{i},\,{\dot {\boldsymbol {r}}}_{i})$ — это релятивистское спутника смещение часов, периодически возрастающее из-за эксцентриситета орбиты Земли и гравитационного поля . Положение и скорость спутника определяются $\displaystyle t_{i}$ следующее: $\displaystyle {\boldsymbol {r}}_{i}\;=\;{\boldsymbol {r}}_{i}(t_{i})$ и $\displaystyle {\dot {\boldsymbol {r}}}_{i}\;=\;{\dot {\boldsymbol {r}}}_{i}(t_{i})$.
4. В области ГНСС «геометрический диапазон» $\displaystyle r({\boldsymbol {r}}_{A},\,{\boldsymbol {r}}_{B})$, определяется как прямой диапазон или трехмерное расстояние , от $\displaystyle {\boldsymbol {r}}_{A}$ к $\displaystyle {\boldsymbol {r}}_{B}$ в инерциальной системе отсчета (например, ECI ), а не во вращающейся системе отсчета .
5. Позиция получателя, $\displaystyle {\boldsymbol {r}}_{\text{rec}}$и время приема, $\displaystyle t_{\text{rec}}$, удовлетворяют светового конуса уравнению $\displaystyle r({\boldsymbol {r}}_{i},\,{\boldsymbol {r}}_{\text{rec}})/c\,+\,(t_{i}-t_{\text{rec}})\;=\;0$ в инерциальной системе отсчёта , где $\displaystyle c$ это скорость света . Время прохождения сигнала от спутника до приемника равно $\displaystyle -(t_{i}\,-\,t_{\text{rec}})$.
6. Вышеизложенное распространяется на спутниковой навигации позиционирования уравнение : $\displaystyle r({\boldsymbol {r}}_{i},\,{\boldsymbol {r}}_{\text{rec}})/c\,+\,(t_{i}\,-\,t_{\text{rec}})\,+\,\delta t_{{\text{atmos}},i}\,-\,\delta t_{{\text{meas-err}},i}\;=\;0$, где $\displaystyle \delta t_{{\text{atmos}},i}$ ( атмосферная задержка = ионосферная задержка + тропосферная задержка ) на пути прохождения сигнала и $\displaystyle \delta t_{{\text{meas-err}},i}$ это погрешность измерения.
7. Метод Гаусса – Ньютона можно использовать для решения нелинейной задачи наименьших квадратов для решения: $\displaystyle ({\hat {\boldsymbol {r}}}_{\text{rec}},\,{\hat {t}}_{\text{rec}})\;=\;\arg \min \phi ({\boldsymbol {r}}_{\text{rec}},\,t_{\text{rec}})$, где $\displaystyle \phi ({\boldsymbol {r}}_{\text{rec}},\,t_{\text{rec}})\;=\;\sum _{i=1}^{n}(\delta t_{{\text{meas-err}},i}/\sigma _{\delta t_{{\text{meas-err}},i}})^{2}$. Обратите внимание, что $\displaystyle \delta t_{{\text{meas-err}},i}$ следует рассматривать как функцию $\displaystyle {\boldsymbol {r}}_{\text{rec}}$ и $\displaystyle t_{\text{rec}}$.
8. распределение Заднее ​ $\displaystyle {\boldsymbol {r}}_{\text{rec}}$ и $\displaystyle t_{\text{rec}}$ пропорционально $\displaystyle \exp(-{\frac {1}{2}}\phi ({\boldsymbol {r}}_{\text{rec}},\,t_{\text{rec}}))$, режим которого $\displaystyle ({\hat {\boldsymbol {r}}}_{\text{rec}},\,{\hat {t}}_{\text{rec}})$. Их вывод формализуется как максимальная апостериорная оценка .
9. распределение Заднее ​ $\displaystyle {\boldsymbol {r}}_{\text{rec}}$ пропорционально $\displaystyle \int _{-\infty }^{\infty }\exp(-{\frac {1}{2}}\phi ({\boldsymbol {r}}_{\text{rec}},\,t_{\text{rec}}))\,dt_{\text{rec}}$.

Чехол с GPS

• Для системы глобального позиционирования (GPS) уравнения незамкнутой формы на шаге 3 приводят к

$\scriptstyle {\begin{cases}\scriptstyle \Delta t_{i}(t_{i},\,E_{i})\;\triangleq \;t_{i}\,+\,\delta t_{{\text{clock}},i}(t_{i},\,E_{i})\,-\,{\tilde {t}}_{i}\;=\;0,\\\scriptstyle \Delta M_{i}(t_{i},\,E_{i})\;\triangleq \;M_{i}(t_{i})\,-\,(E_{i}\,-\,e_{i}\sin E_{i})\;=\;0,\end{cases}}$

в котором $\scriptstyle E_{i}$ — орбитальная эксцентрическая аномалия спутника $i$, $\scriptstyle M_{i}$ это средняя аномалия , $\scriptstyle e_{i}$ - это эксцентриситет , и $\scriptstyle \delta t_{{\text{clock}},i}(t_{i},\,E_{i})\;=\;\delta t_{{\text{clock,sv}},i}(t_{i})\,+\,\delta t_{{\text{orbit-relativ}},i}(E_{i})$.

• Вышеуказанное можно решить, используя двумерный Ньютона – Рафсона . метод $\scriptstyle t_{i}$ и $\scriptstyle E_{i}$. В большинстве случаев две итерации будут необходимы и достаточны. Его итеративное обновление будет описано с использованием аппроксимированной обратной матрицы Якоби следующим образом:

$\scriptstyle {\begin{pmatrix}t_{i}\\E_{i}\\\end{pmatrix}}\leftarrow {\begin{pmatrix}t_{i}\\E_{i}\\\end{pmatrix}}-{\begin{pmatrix}1&&0\\{\frac {{\dot {M}}_{i}(t_{i})}{1-e_{i}\cos E_{i}}}&&-{\frac {1}{1-e_{i}\cos E_{i}}}\\\end{pmatrix}}{\begin{pmatrix}\Delta t_{i}\\\Delta M_{i}\\\end{pmatrix}}$

• Тропосферную задержку нельзя игнорировать, хотя спецификация системы глобального позиционирования (GPS) не дает его подробного описания.

Дело ГЛОНАСС

• Эфемериды ГЛОНАСС . не обеспечивают смещения часов $\scriptstyle \delta t_{{\text{clock,sv}},i}(t)$, но $\scriptstyle \delta t_{{\text{clock}},i}(t)$.

См. также

• Время сначала исправить

Примечания

• В области ГНСС $\scriptstyle {\tilde {r}}_{i}\;=\;-c({\tilde {t}}_{i}\,-\,{\tilde {t}}_{\text{rec}})$ называется псевдодальностью , где $\scriptstyle {\tilde {t}}_{\text{rec}}$ — предварительное время приема получателя. $\scriptstyle \delta t_{\text{clock,rec}}\;=\;{\tilde {t}}_{\text{rec}}\,-\,t_{\text{rec}}$ называется смещением тактового сигнала приемника (т.е. опережением тактового сигнала).
• Стандартный выход приемников GNSS $\scriptstyle {\tilde {r}}_{i}$ и $\scriptstyle {\tilde {t}}_{\text{rec}}$ наблюдения за эпоху .
• Временное изменение смещения релятивистских часов спутника является линейным, если его орбита круговая (и, следовательно, его скорость однородна в инерциальной системе отсчета).
• Время прохождения сигнала от спутника до приемника выражается как $\scriptstyle -(t_{i}-t_{\text{rec}})\;=\;{\tilde {r}}_{i}/c\,+\,\delta t_{{\text{clock}},i}\,-\,\delta t_{\text{clock,rec}}$, правая часть которого во время расчета является резистивной по отношению к ошибке округления .
• Геометрический диапазон рассчитывается как $\scriptstyle r({\boldsymbol {r}}_{i},\,{\boldsymbol {r}}_{\text{rec}})\;=\;|\Omega _{\text{E}}(t_{i}\,-\,t_{\text{rec}}){\boldsymbol {r}}_{i,{\text{ECEF}}}\,-\,{\boldsymbol {r}}_{\text{rec,ECEF}}|$, где геоцентрическая, геофиксированная вращающаяся система координат (ECEF) (например, WGS84 или ITRF ) используется с правой стороны и $\scriptstyle \Omega _{\text{E}}$ – матрица вращения Земли с аргументом времени прохождения сигнала . Матрицу можно факторизовать как $\scriptstyle \Omega _{\text{E}}(t_{i}\,-\,t_{\text{rec}})\;=\;\Omega _{\text{E}}(\delta t_{\text{clock,rec}})\Omega _{\text{E}}(-{\tilde {r}}_{i}/c\,-\,\delta t_{{\text{clock}},i})$.
• Единичный вектор прямой видимости спутника, наблюдаемого на $\scriptstyle {\boldsymbol {r}}_{\text{rec,ECEF}}$ описывается как: $\scriptstyle {\boldsymbol {e}}_{i,{\text{rec,ECEF}}}\;=\;-{\frac {\partial r({\boldsymbol {r}}_{i},\,{\boldsymbol {r}}_{\text{rec}})}{\partial {\boldsymbol {r}}_{\text{rec,ECEF}}}}$.
• Уравнение спутниковой навигации позиционирования можно выразить с помощью переменных $\scriptstyle {\boldsymbol {r}}_{\text{rec,ECEF}}$ и $\scriptstyle \delta t_{\text{clock,rec}}$.
• Нелинейность итерациях Гаусса – вертикальной зависимости тропосферной задержки ухудшает эффективность сходимости в Ньютона на шаге 7.
• Приведенные выше обозначения отличаются от обозначений в статьях Википедии «Введение в расчет положения» и «Расширенный расчет положения» Глобальной системы позиционирования (GPS).

См. также

• Снижение точности (навигация)
• Глобальная система позиционирования § Уравнения навигации
• Корректировка методом наименьших квадратов
• Точное позиционирование точки
• Кинематика в реальном времени

Внешние ссылки

• PVT (положение, скорость, время): процедура расчета в GNSS-SDR с открытым исходным кодом и базовой RTKLIB.