Двумерный анализ

Время ожидания между извержениями и продолжительность извержения гейзера Old Faithful в Йеллоустонском национальном парке , штат Вайоминг , США. Эта диаграмма рассеяния предполагает, что обычно существует два «типа» извержений: кратковременные и кратковременные и длительные и длительные.

Двумерный анализ — одна из простейших форм количественного (статистического) анализа . ^[1] Он включает в себя анализ двух переменных (часто обозначаемых как X , Y ) с целью определения эмпирической связи между ними. ^[1]

быть полезен при проверке простых гипотез связи Двумерный анализ может . Двумерный анализ может помочь определить, в какой степени становится легче узнать и предсказать значение одной переменной (возможно, зависимой переменной ), если мы знаем значение другой переменной (возможно, независимой переменной ) (см. также корреляцию и простую линейную регрессию ). . ^[2]

Двумерный анализ можно противопоставить одномерному анализу , при котором анализируется только одна переменная. ^[1] Как и одномерный анализ, двумерный анализ может быть описательным или логическим . Это анализ взаимосвязи между двумя переменными. ^[1] Двумерный анализ — это простой (с двумя переменными) частный случай многомерного анализа (когда одновременно исследуются множественные отношения между несколькими переменными). ^[1]

Двумерная регрессия

Регрессия — это статистический метод, используемый для исследования того, как изменение одной или нескольких переменных предсказывает или объясняет изменение другой переменной. Двумерная регрессия направлена на определение уравнения, представляющего оптимальную линию, которая определяет взаимосвязь между двумя переменными на основе определенного набора данных. Это уравнение впоследствии применяется для прогнозирования значений зависимой переменной, отсутствующей в исходном наборе данных. С помощью регрессионного анализа можно вывести уравнение кривой или прямой линии и получить коэффициент корреляции.

Простая линейная регрессия

Простая линейная регрессия — это статистический метод, используемый для моделирования линейной зависимости между независимой переменной и зависимой переменной. Он предполагает линейную связь между переменными и чувствителен к выбросам. Наиболее подходящее линейное уравнение часто представляется в виде прямой линии, чтобы минимизировать разницу между прогнозируемыми значениями уравнения и фактическими наблюдаемыми значениями зависимой переменной.

Уравнение: $y=mx+b$

$x$ : независимая переменная (предиктор)

$y$ : зависимая переменная (результат)

$m$ : наклон линии

$b$ : $y$ -перехват

Линия регрессии наименьших квадратов (LSRL)

Линия регрессии по методу наименьших квадратов — это метод простой линейной регрессии для моделирования линейной зависимости между двумя переменными, который служит инструментом для прогнозирования на основе новых значений независимой переменной. Расчет основан на методе критерия наименьших квадратов . Цель состоит в том, чтобы минимизировать сумму квадратов вертикальных расстояний (остатков) между наблюдаемыми значениями y и соответствующими прогнозируемыми значениями y для каждой точки данных.

Двумерная корреляция

Двумерная корреляция — это мера того, являются ли две переменные коковарными и если да, то каким образом, то есть изменяется ли дисперсия одной линейно по мере изменения дисперсии другой.

Ковариацию может быть сложно интерпретировать в разных исследованиях, поскольку она зависит от масштаба или уровня используемых измерений. По этой причине ковариация стандартизируется путем деления на произведение стандартных отклонений двух переменных для получения коэффициента корреляции произведения и момента Пирсона (также называемого коэффициентом корреляции Пирсона или коэффициентом корреляции), который обычно обозначается буквой « р ». ^[3]

Коэффициент корреляции Пирсона используется, когда обе переменные измеряются по шкале интервалов или отношений. Другие коэффициенты корреляции или анализы используются, когда переменные не являются интервалами или отношениями или когда они не имеют нормального распределения. Примерами являются коэффициент корреляции Спирмена , тау Кендалла , бисериальная корреляция и анализ хи-квадрат.

В отношении корреляции следует выделить три важных замечания:

Наличие выбросов может серьезно исказить коэффициент корреляции.
Большие размеры выборки могут привести к статистически значимым корреляциям, которые могут иметь небольшое практическое значение или вообще не иметь его.
Невозможно сделать выводы о причинно-следственной связи, основываясь только на корреляционном анализе.

Когда есть зависимая переменная

Если зависимая переменная — та, значение которой в некоторой степени определяется другой независимой переменной — является категориальной переменной , например, предпочтительной маркой зерновых, то пробит- или логит- регрессию (или полиномиальную пробит- или полиномиальную логит-регрессию можно использовать ). . Если обе переменные являются порядковыми , то есть они ранжируются в последовательности как первая, вторая и т. д., то ранговой корреляции можно вычислить коэффициент . Если только зависимая переменная является порядковой, упорядоченный пробит или упорядоченный логит можно использовать . Если зависимая переменная является непрерывной (либо уровень интервала, либо уровень соотношения, например, шкала температуры или шкала доходов), то простую регрессию можно использовать .

Если обе переменные представляют собой временные ряды определенный тип причинности, известный как причинность Грейнджера , можно проверить векторную авторегрессию , и выполнить для изучения межвременных связей между переменными.

Когда нет зависимой переменной

Когда ни одна переменная не может рассматриваться как зависимая от другой, регрессия не подходит, но может подойти некоторая форма корреляционного анализа. ^[4]

Графические методы

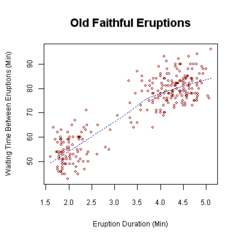
Графики , подходящие для двумерного анализа, зависят от типа переменной. Для двух непрерывных переменных диаграмма рассеяния представляет собой обычный график. Когда одна переменная является категориальной, а другая — непрерывной, ящичковая диаграмма обычно используется мозаичная диаграмма , а когда обе переменные являются категориальными , обычно используется . Эти графики являются частью описательной статистики .

См. также

Внешние ссылки

Дискриминантно-корреляционный анализ (DCA) ^[5]

Ссылки

^ Перейти обратно: ^а ^б ^с ^д ^и Эрл Р. Бэбби , Практика социальных исследований , 12-е издание, Wadsworth Publishing, 2009 г., ISBN 0-495-59841-0 , стр. 436–440.
^ Двумерный анализ , Социологический индекс
^ Сандилендс, Дебра (Далли) (2014). «Энциклопедия исследований качества жизни и благополучия, двумерный анализ, стр. 416–418» . СпрингерЛинк .
^ Чаттерджи, Самприт (2012). Регрессионный анализ на примере . Хобокен, Нью-Джерси: Уайли. ISBN 978-0470905845 .
^ М. Хагигат, М. Абдель-Мотталеб и В. Альхалаби (2016). Дискриминантный корреляционный анализ: объединение уровней признаков в реальном времени для мультимодального биометрического распознавания . Транзакции IEEE по информационной криминалистике и безопасности, 11 (9), 1984–1996.

[babbie-1] Перейти обратно: ^а ^б ^с ^д ^и Эрл Р. Бэбби , Практика социальных исследований , 12-е издание, Wadsworth Publishing, 2009 г., ISBN 0-495-59841-0 , стр. 436–440.

[2] Двумерный анализ , Социологический индекс

[:0-3] Сандилендс, Дебра (Далли) (2014). «Энциклопедия исследований качества жизни и благополучия, двумерный анализ, стр. 416–418» . СпрингерЛинк .

[Chaterjee-4] Чаттерджи, Самприт (2012). Регрессионный анализ на примере . Хобокен, Нью-Джерси: Уайли. ISBN 978-0470905845 .

[dca-5] М. Хагигат, М. Абдель-Мотталеб и В. Альхалаби (2016). Дискриминантный корреляционный анализ: объединение уровней признаков в реальном времени для мультимодального биометрического распознавания . Транзакции IEEE по информационной криминалистике и безопасности, 11 (9), 1984–1996.

[1]

[2]

[3]

[4]

[5]