Тетрада (геометрическая головоломка)

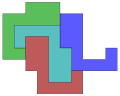
Тетрада с одной центральной областью и тремя окружающими.	Тетрада с дыркой

В геометрии тетрада — это набор из четырех односвязных непересекающихся плоских областей на плоскости, каждая пара имеет конечную часть общей границы. Он был назван Майклом Р.В. Бакли в 1975 году в Журнале занимательной математики . Был предложен еще один вопрос, который стал загадкой: могут ли эти 4 области быть конгруэнтными, с дырками или без них , другим закрытым областям. ^{[ 1 ]}

Наименьшее количество сторон и вершин

Решения с четырьмя конгруэнтными плитками включают в себя решения с пятью сторонами. ^{[ 2 ]} Однако их размещение окружает незакрытую дыру в плоскости. Среди решений без дырок решения с наименьшим возможным количеством сторон представляют собой шестиугольник, который Скотт Ким определил как студент Стэнфордского университета. ^{[ 1 ]} Неизвестно, возможны ли пятисторонние решения без дырок. ^{[ 2 ]}

Решение Кима имеет 16 вершин, в то время как некоторые решения пятиугольника имеют всего 11 вершин. Неизвестно, возможно ли меньшее количество вершин. ^{[ 2 ]}

Конгруэнтные полиформные решения

Гарднер предложил ряд полиформных решений ( полиамино , полиалмаз и полигекс ) без отверстий. ^{[ 1 ]}

11 квадратов
12 квадратов
10 треугольников
22 треугольника
26 треугольников
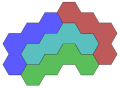
4 шестиугольника

Ссылки

^ Jump up to: ^а ^б ^с Мартин Гарднер, «От плиток Пенроуза к шифрам с люком» , 1989, стр.121–123 [1]
^ Jump up to: ^а ^б ^с Дополнительные вопросы о тетрадах Уолтера Трампа

Внешние ссылки

Полиформные тетрады , полимино и полинарные тетрады
Пазл тетрады 7 апреля 2020 г.
Применение информационных технологий в математических доказательствах и проверке результатов исследований учащихся
Тетрады и их счет Юрис ЧЕРНЕНОКС, Андрей ЦИБУЛИС

Эта посвященная геометрии, статья, незавершена . Вы можете помочь Википедии, расширив ее .

[gardner-1] Jump up to: ^а ^б ^с Мартин Гарднер, «От плиток Пенроуза к шифрам с люком» , 1989, стр.121–123 [1]

[trump-2] Jump up to: ^а ^б ^с Дополнительные вопросы о тетрадах Уолтера Трампа

[ 1 ]

[ 2 ]