Полигекс (математика)

В развлекательной математике многогекс — это многогранная форма с правильным шестиугольником (или для краткости «шестиугольник») в качестве базовой формы, построенная путем соединения одного или нескольких шестиугольников. Конкретные формы названы по количеству шестиугольников: моногекс , дигекс , тригекс , тетрагекс и т. д. Названия им дал Дэвид Кларнер, исследовавший их.
Каждая отдельная многогранная плитка и многогексы тесселяции могут быть нарисованы на регулярной шестиугольной плитке .
Правила строительства
[ редактировать ]Правила соединения шестиугольников могут различаться. Однако в целом применяются следующие правила:
- Два шестиугольника могут быть соединены только по общему краю и должны иметь всю эту сторону.
- Никакие два шестиугольника не могут перекрываться.
- Полигекс должен быть связан. Конфигурации несвязанных базовых многоугольников не считаются многогексами.
- Зеркальное изображение асимметричного многоугольника не считается отдельным многоугольником (многогексы «двусторонние»).
Свойства тесселяции
[ редактировать ]
Все многогексы с числом шестиугольников менее пяти могут образовывать хотя бы одну правильную плоскую мозаику.
Кроме того, плоские мозаики дигекса и прямых многогексов инвариантны при вращении или отражении на 180 градусов параллельно или перпендикулярно длинной оси дигекса (симметрия вращения 2-го порядка и симметрия отражения 4-го порядка), а также мозаика шестиугольников и некоторых других многогексов ( как шестигранник с одним отверстием ниже) инвариантны при вращении на 60, 120 или 180 градусов (вращательная и отражательная симметрия 6-го порядка).
Кроме того, шестиугольник является шестигранником , поэтому все полигексы также являются отдельными полиалмазами . Кроме того, поскольку равносторонний треугольник представляет собой шестиугольник и три равносторонних треугольника меньшего размера, можно наложить большой многоугольник на любой многоугольник, получив два многоугольника, соответствующие каждому многоугольнику. Это используется как основа бесконечного деления шестиугольника на все меньшие и меньшие шестиугольники (неповторяющаяся мозаика) или на шестиугольники и треугольники.
Перечисление
[ редактировать ]


Как и в случае с полимино , многогексы могут быть нумерованы как свободные многогексы (где повороты и отражения считаются одной и той же формой), фиксированные многогексы (где разные ориентации считаются разными) и односторонние многогексы (где зеркальные изображения считаются разными, а повороты считаются идентичными). ). Их также можно различать по тому, могут ли они содержать отверстия. Количество свободных n -гексов для n = 1, 2, 3,… равно 1, 1, 3, 7, 22, 82, 333, 1448, … (последовательность A000228 в OEIS ); количество свободных многогексов с дырками определяется OEIS : A038144 ; количество свободных многогексов без дырок определяется OEIS : A018190 ; количество односторонних многоугольников определяется OEIS : A006535 ; количество фиксированных многоугольников определяется OEIS : A001207 . [1] [2]
| н | Бесплатно | Свободный с дырками. | Бесплатно, без дырок. | Односторонний | Зафиксированный |
|---|---|---|---|---|---|
| 1 | 1 | 0 | 1 | 1 | 1 |
| 2 | 1 | 0 | 1 | 1 | 3 |
| 3 | 3 | 0 | 3 | 3 | 11 |
| 4 | 7 | 0 | 7 | 10 | 44 |
| 5 | 22 | 0 | 22 | 33 | 186 |
| 6 | 82 | 1 | 81 | 147 | 814 |
| 7 | 333 | 2 | 331 | 620 | 3652 |
| 8 | 1448 | 13 | 1435 | 2821 | 16689 |
| 9 | 6572 | 67 | 6505 | 12942 | 77359 |
| 10 | 30490 | 404 | 30086 | 60639 | 362671 |
Симметрия
[ редактировать ]Из многогексов вплоть до шестигексов 2 имеют 6-кратную симметрию вращения и отражения (следовательно, также 3-кратную и 2-кратную симметрию), моногекс и шестиугольник с отверстием, 3 других имеют 3-кратное вращение (компактный трехгранник, четырехугольник пропеллера и шестиугольник, похожий на равносторонний треугольник) и 3-кратную симметрию отражения, 9 других имеют 2-кратное вращение и отражение, 8 имеют только 2-кратное вращение, 16 имеют только 2-кратное отражение, а остальные 78 (большая часть тетрагексы, пентагексы или шестигексы) асимметричны. Замощения большинства отражательно-симметричных многогексов также инвариантны относительно скользящих отражений того же порядка по длине многогекса.
Моногексы
[ редактировать ]Есть один моногекс. Он замостит плоскость как обычную шестиугольную мозаику .
Дигексы
[ редактировать ]Существует один свободный дигекс:
Тригексы
[ редактировать ]Есть 3 свободных и двусторонних тригекса:
Тетрагексы
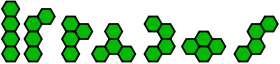
[ редактировать ]Всего имеется 7 свободных и двусторонних тетрагексов. Им даны имена в указанном порядке: брусок, червь, пистолет, пропеллер, арка, пчела и волна. [3]
Пятигексы
[ редактировать ]Есть 22 свободных и двусторонних пентагекса:
Шестигранники
[ редактировать ]Всего имеется 82 свободных и двусторонних шестиугольника:
См. также
[ редактировать ]- Тесселяция
- Теория перколяции
- Полиалмаз – мозаика с равносторонними треугольниками.
- Полимино – мозаика с квадратами
- Полициклические ароматические углеводороды - углеводороды, структура которых основана на полигексах.
- Рептилии - мозаики фигур, состоящие из уменьшенных копий самих себя.
Ссылки
[ редактировать ]- ^ Wolfram Mathworld: Polyhex
- ^ Гленн К. Роудс, Плоские мозаики полимино, полигексами и полиалмазами, Журнал вычислительной и прикладной математики 174 (2005), № 2, стр. 329–353
- ^ Гарднер, М. Математическое магическое шоу: больше головоломок, игр, развлечений, иллюзий и других математических уловок от Scientific American. Нью-Йорк: Винтаж, с. 147, 1978. PDF