Октамино

Октамино ; (или 8-омино ) — это полимино 8-го порядка то есть многоугольник на плоскости, одинакового размера состоящий из 8 квадратов , соединенных ребром к краю. ^[1] Если вращения и отражения не считать отдельными формами, существует 369 различных свободных октамино. Когда отражения считаются отдельными, получается 704 односторонних октамино. Если вращения также считаются отдельными, существует 2725 фиксированных октамино. ^[2]^[3]

Симметрия

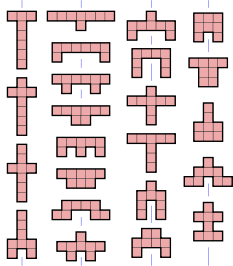
На рисунке показаны все возможные свободные октамино, раскрашенные в соответствии с их группами симметрии :

316 октамино (серого цвета) не имеют симметрии . Их группа симметрии состоит только из тождественного отображения .
23 октамино (красного цвета) имеют ось симметрии отражения, совмещенную с линиями сетки. Их группа симметрии состоит из двух элементов: единицы и отражения в линии, параллельной сторонам квадратов.

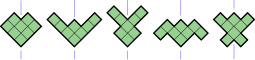
5 октамино (зеленого цвета) имеют ось симметрии отражения под углом 45 ° к линиям сетки. Их группа симметрии состоит из двух элементов: единицы и диагонального отражения.

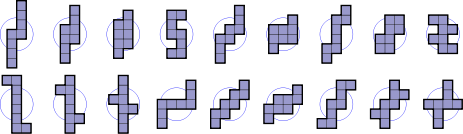
18 октамино (синего цвета) обладают точечной симметрией, также известной как вращательная симметрия второго порядка. Их группа симметрии состоит из двух элементов: единицы и поворота на 180°.

1 октамино (желтого цвета) имеет вращательную симметрию четвертого порядка. Его группа симметрии состоит из четырех элементов: единицы и поворотов на 90 °, 180 ° и 270 °.

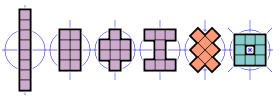
4 октамино (фиолетового цвета) имеют две оси симметрии отражения, обе выровнены по линиям сетки. Их группа симметрии состоит из четырех элементов: единицы, двух отражений и поворота на 180°. Это группа диэдра второго порядка, также известная как четырехгруппа Клейна .
1 октамино (оранжевого цвета) имеет две оси симметрии отражения, обе выровнены по диагоналям. Его группа симметрии также представляет собой группу диэдра второго порядка с четырьмя элементами.
1 октамино (голубой цвет) имеет четыре оси симметрии отражения, выровненные по линиям сетки и диагоналям, а также вращательную симметрию 4-го порядка. Его группа симметрии, группа диэдра 4-го порядка, состоит из восьми элементов.

Набор октамино — это наименьший набор полимино, в котором реализуются все восемь возможных симметрий. Следующим более высоким набором с этим свойством является набор додекомино (12 омино). ^[3]

Если отражения октамино считаются отдельными, как и в случае с односторонними октамино, то размеры первой, четвертой и пятой категорий выше удваиваются, что приводит к дополнительным 335 октамино, всего 704. Если вращения также считаются отдельными, затем октамино из первой категории считаются восьмикратными, октамино из следующих трех категорий считаются четырехкратными, октамино из категорий с пятой по седьмую считаются дважды, а последнее октамино учитывается только один раз. В результате получается 316 × 8 + (23+5+18) × 4 + (1+4+1) × 2 + 1 = 2725 фиксированных октамино.

Упаковка и укладка плитки

Из 369 свободных октамино 320 удовлетворяют критерию Конвея и еще 23 могут образовать участок, удовлетворяющий критерию. ^[4] Остальные 26 октамино (в том числе 6 с дырками) не могут мозаику плоскости. ^[5]

Поскольку в 6 свободных октамино есть дырка, нетрудно доказать, что полный набор октамино нельзя упаковать в прямоугольник и что не все октамино можно выложить плиткой .

Ссылки

^ Голомб, Соломон В. (1994). Полимино (2-е изд.). Принстон, Нью-Джерси: Издательство Принстонского университета. ISBN 0-691-02444-8 .
^ Вайсштейн, Эрик В. «Октамино» . Из MathWorld — веб-ресурса Wolfram . Проверено 22 июля 2008 г.
^ Jump up to: Перейти обратно: ^а ^б Редельмайер, Д. Хью (1981). «Подсчет полимино: еще одна атака» . Дискретная математика . 36 (2): 191–203. дои : 10.1016/0012-365X(81)90237-5 .
^ Роудс, Гленн К. (2005). «Плоские замощения полимино, полигексами и полиалмазами». Журнал вычислительной и прикладной математики . 174 (2): 329–353. дои : 10.1016/j.cam.2004.05.002 .
^ Гарднер, Мартин (август 1975 г.). «Подробнее о замощении плоскости: возможности полимино, полиалмазов и полигексов». Научный американец . 233 (2): 112–115.

[1] Голомб, Соломон В. (1994). Полимино (2-е изд.). Принстон, Нью-Джерси: Издательство Принстонского университета. ISBN 0-691-02444-8 .

[2] Вайсштейн, Эрик В. «Октамино» . Из MathWorld — веб-ресурса Wolfram . Проверено 22 июля 2008 г.

[Redelmeier-3] Jump up to: Перейти обратно: ^а ^б Редельмайер, Д. Хью (1981). «Подсчет полимино: еще одна атака» . Дискретная математика . 36 (2): 191–203. дои : 10.1016/0012-365X(81)90237-5 .

[4] Роудс, Гленн К. (2005). «Плоские замощения полимино, полигексами и полиалмазами». Журнал вычислительной и прикладной математики . 174 (2): 329–353. дои : 10.1016/j.cam.2004.05.002 .

[5] Гарднер, Мартин (август 1975 г.). «Подробнее о замощении плоскости: возможности полимино, полиалмазов и полигексов». Научный американец . 233 (2): 112–115.

[1]

[2]

[3]

[4]

[5]

v т и Полиформы
Полимино	Домино Тромино Тетромино Пентамино Гексомино Гептомино Октамино Нономино декомино
Высшие измерения	Полиоминоид Поликуб
Другие	Поляболо Полиграфтер Полигекс Полиалмаз Псевдополимино Полистик
Игры и головоломки	Блоки Кубик сомы Змеиный куб Танграм Гексастикс Тантрикс Тетрис
ВикиПроект Портал