Гауссовская сетевая модель

Рисунок 1: Модель гауссовой сети (GNM) представление основной частицы нуклеосомы (идентификатор PDB: 1KX4). Шарики/узлы представляют собой остатки (аминокислоты, серые; и нуклеотиды при их Р (оранжевый), С4'- и С2-атомах (белые). Узлы соединены упругими пружинами (светло-серые для внутримолекулярных белков, желтые для внутримолекулярных белков). Внутримолекулярная ДНК/РНК и циан (межмолекулярный белок-ДНК).

Модель гауссовой сети (GNM) представляет собой представление биологической макромолекулы как упругой сети масс и пружин для изучения, понимания и характеристики механических аспектов ее долгосрочной крупномасштабной динамики . Модель имеет широкий спектр применений: от небольших белков, таких как ферменты, состоящие из одного домена , до крупных макромолекулярных ансамблей, таких как рибосома или вирусный капсид . Динамика белковых доменов играет ключевую роль во множестве процессов молекулярного распознавания и передачи сигналов в клетках .Белковые домены, соединенные внутренне неупорядоченными гибкими линкерными доменами, индуцируют дальнюю аллостерию посредством динамики белковых доменов .Получающиеся в результате динамические режимы обычно не могут быть предсказаны на основе статических структур ни всего белка, ни отдельных доменов.

Сетевая модель Гаусса — это минималистский, крупнозернистый подход к изучению биологических молекул. В модели белки представлены узлами, соответствующими α-углеродам аминокислотных остатков. Аналогично структуры ДНК и РНК представлены от одного до трех узлов на каждый нуклеотид . Модель использует гармоническое приближение для моделирования взаимодействий. Такое крупнозернистое представление делает вычисления недорогими в вычислительном отношении.

На молекулярном уровне многие биологические явления, такие как каталитическая активность фермента , происходят в диапазоне от нано-до миллисекунд. Все методы моделирования атомов, такие как моделирование молекулярной динамики , редко достигают микросекундной длины траектории, в зависимости от размера системы и доступных вычислительных ресурсов. Анализ нормального режима в контексте моделей GNM или моделей упругой сети (EN) в целом дает представление о более крупномасштабном функциональном динамическом поведении макромолекул. Здесь модель отражает функциональные движения биомолекулы в естественном состоянии за счет атомных деталей. Выводы, полученные на основе этой модели, дополняют методы моделирования атомарных деталей.

Другая модель динамики белков, основанная на упругих сетях масс и пружин, — это модель анизотропной сети .

Теория модели гауссовской сети

Рисунок 2: Схематическое изображение узлов эластичной сети GNM. Каждый узел связан со своими пространственными соседями едиными пружинами. Вектор расстояния между двумя узлами i и j показан стрелкой и помечен R _ij . Положения равновесия i -го и j -го узлов, R ⁰ _я и Р ⁰ _j показаны в системе координат xyz. Р ⁰ _ij — равновесное расстояние между узлами i и j . Векторы мгновенных колебаний ΔR _i и ΔR _j и мгновенный вектор расстояния R _ij показаны пунктирными стрелками.

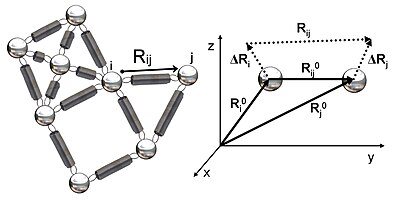
Модель гауссовской сети была предложена Бахаром, Атилганом, Халилоглу и Эрманом в 1997 году. GNM часто анализируется с использованием анализа нормального режима, который предлагает аналитическую формулировку и уникальное решение для каждой структуры. Анализ нормального режима GNM отличается от других анализов нормального режима тем, что он основан исключительно на топологии контакта между остатками, находящейся под влиянием теории упругости Флори. и модель Роуз и не учитывает трехмерную направленность движений.

Представление структуры в виде эластичной сети

На рисунке 2 показано схематическое изображение эластичной сети, изучаемой в GNM. Металлические бусины представляют собой узлы этой гауссовой сети (остатки белка), а пружины представляют собой связи между узлами (ковалентные и нековалентные взаимодействия между остатками). Для узлов i и j векторы положения равновесия R ⁰ _я и Р ⁰ _j , вектор равновесного расстояния, R ⁰ _ij , мгновенные векторы колебаний, ΔR _i и ΔR _j , и мгновенный вектор расстояния, R _ij , показаны на рисунке 2. Мгновенные векторы положения этих узлов определяются R _i и R _j . Разница между вектором положения равновесия и вектором мгновенного положения остатка i дает вектор мгновенных колебаний ΔR _i = R _i - R. ⁰ _я . Следовательно, мгновенный вектор колебаний между узлами i и j выражается как ΔR _ij = ΔR _j - ΔR _i = R _ij - R ⁰ _я .

Потенциал гауссовой сети

Потенциальная энергия сети через ΔR _i равна

$V_{GNM}={\frac {\gamma }{2}}\left[\sum _{i,j}^{N}(\Delta R_{j}-\Delta R_{i})^{2}\right]={\frac {\gamma }{2}}\left[\sum _{i,j}^{N}\Delta R_{i}\Gamma _{ij}\Delta R_{j}\right]$

где γ — силовая постоянная, равномерная для всех пружин, а Γ _ij — ij -й элемент матрицы Кирхгофа (или матрицы связности) контактов между остатками, Γ , определяемый формулой

$\Gamma _{ij}=\left\{{\begin{matrix}-1,&{\mbox{if }}i\neq j&{\mbox{and }}R_{ij}\leq r_{c}\\0,&{\mbox{if }}i\neq j&{\mbox{and }}R_{ij}>r_{c}\\-\sum _{j,j\neq i}^{N}\Gamma _{ij},&{\mbox{if }}i=j\end{matrix}}\right.$

r _c представляет собой предельное расстояние для пространственных взаимодействий и принимается равным 7 Å для пар аминокислот (представленных их α-углеродами).

Выражая компоненты X, Y и Z векторов колебаний ΔR _i как ΔX ^Т = [ΔX ₁ ΔX ₂ ..... ΔX _N ], ΔY ^Т = [ΔY ₁ ΔY ₂ ..... ΔY _N ], и ΔZ ^Т = [ΔZ ₁ ΔZ ₂ ..... ΔZ _N ], приведенное выше уравнение упрощается до

$V_{GNM}={\frac {\gamma }{2}}[\Delta X^{T}\Gamma \Delta X+\Delta Y^{T}\Gamma \Delta Y+\Delta Z^{T}\Gamma \Delta Z]$

Основы статистической механики

В GNM распределение вероятностей всех флуктуаций P ( ΔR ) изотропно.

$P(\Delta R)=P(\Delta X,\Delta Y,\Delta Z)=p(\Delta X)p(\Delta Y)p(\Delta Z)$

и гауссовский

$p(\Delta X)\propto \exp \left\{-{\frac {\gamma }{2k_{B}T}}\Delta X^{T}\Gamma \Delta X\right\}=\exp \left\{-{\frac {1}{2}}\left(\Delta X^{T}\left({\frac {k_{B}T}{\gamma }}\Gamma ^{-1}\right)^{-1}\Delta X\right)\right\}$

где k _B — постоянная Больцмана, а T — абсолютная температура. p ( ΔY ) и p ( ΔZ ) выражаются аналогично. N-мерная функция плотности вероятности Гаусса с вектором случайной величины x , средним вектором µ и ковариационной матрицей Σ равна

$W(x,\mu ,\Sigma )={\frac {1}{\sqrt {(2\pi )^{N}|\Sigma |}}}\exp \left\{-{\frac {1}{2}}(x-\mu )^{T}\Sigma ^{-1}(x-\mu )\right\}$

${\sqrt {(2\pi )^{N}|\Sigma |}}$ нормализует распределение и |Σ| является определителем ковариационной матрицы.

Подобно распределению Гаусса, нормализованное распределение для ΔX ^Т = [ΔX ₁ ΔX ₂ ..... ΔX _N ] вокруг положений равновесия можно выразить как

$p(\Delta X)={\frac {1}{\sqrt {(2\pi )^{N}{\frac {k_{B}T}{\gamma }}|\Gamma ^{-1}|}}}\exp \left\{-{\frac {1}{2}}\left(\Delta X^{T}\left({\frac {k_{B}T}{\gamma }}\Gamma ^{-1}\right)^{-1}\Delta X\right)\right\}$

Константа нормализации, а также статистическая сумма Z _X , определяется выражением

$Z_{X}=\int _{0}^{\infty }\exp \left\{-{\frac {1}{2}}\left(\Delta X^{T}\left({\frac {k_{B}T}{\gamma }}\Gamma ^{-1}\right)^{-1}\Delta X\right)\right\}d\Delta X$

где ${\frac {k_{B}T}{\gamma }}\Gamma ^{-1}$ в данном случае это ковариационная матрица. Z _Y и Z _Z выражаются аналогично. Эта формулировка требует обращения матрицы Кирхгофа. В GNM определитель матрицы Кирхгофа равен нулю, поэтому вычисление ее обратного требует разложения по собственным значениям . Γ ⁻¹ строится с использованием N-1 ненулевых собственных значений и связанных с ними собственных векторов. Выражения для p ( ΔY ) и p ( ΔZ ) аналогичны выражениям для p ( ΔX ). Распределение вероятностей всех колебаний в GNM становится

$P(\Delta R)=p(\Delta X)p(\Delta Y)p(\Delta Z)={\frac {1}{{Z_{X}}{Z_{Y}}{Z_{Z}}}}\exp \left\{-{\frac {3}{2}}\left(\Delta X^{T}\left({\frac {k_{B}T}{\gamma }}\Gamma ^{-1}\right)^{-1}\Delta X\right)\right\}$

Для этой системы масс и пружин константа нормализации в предыдущем выражении представляет собой общую статистическую сумму GNM, Z _GNM ,

$Z_{GNM}={Z_{X}}{Z_{Y}}{Z_{Z}}={(2\pi )^{3N/2}{\Biggl |}{{\frac {k_{B}T}{\gamma }}{\Gamma ^{-1}}}{\Biggr |}}^{3/2}$

Ожидаемые значения колебаний и корреляций

Ожидаемые значения колебаний остатка, < ΔR _i ² > (также называемые среднеквадратичными флуктуациями, MSF) и их взаимные корреляции < ΔR _i · ΔR _j > могут быть организованы как диагональные и недиагональные члены, соответственно, ковариационной матрицы. На основе статистической механики ковариационная матрица для ΔX определяется выражением

$<\Delta X\cdot \Delta X^{T}>=\int \Delta X\cdot \Delta X^{T}p(\Delta X)d\Delta X={\frac {k_{B}T}{\gamma }}\Gamma ^{-1}$

Последнее равенство получается путем подстановки приведенного выше p( ∆X ) и принятия (обобщенного гауссова) интеграла. С,

$<\Delta X\cdot \Delta X^{T}>=<\Delta Y\cdot \Delta Y^{T}>=<\Delta Z\cdot \Delta Z^{T}>={\frac {1}{3}}<\Delta R\cdot \Delta R^{T}>$

< ΔR _я ² > и < ΔR _i · ΔR _j > следует

$<\Delta R_{i}^{2}>={\frac {3k_{B}T}{\gamma }}(\Gamma ^{-1})_{ii}$

$<\Delta R_{i}\cdot \Delta R_{j}>={\frac {3k_{B}T}{\gamma }}(\Gamma ^{-1})_{ij}$

Разложение по модам

Нормальные моды ГНМ находятся путем диагонализации матрицы Кирхгофа Γ = UΛU ^Т . Здесь U — унитарная матрица, U ^Т = У ⁻¹ собственных векторов u _i Γ Λ и i является диагональной матрицей собственных значений λ _. , Частота и форма моды представлены ее собственным значением и собственным вектором соответственно. Поскольку матрица Кирхгофа положительно полуопределена, первое собственное значение λ ₁ равно нулю, а все элементы соответствующего собственного вектора равны 1/ √ N . Это показывает, что сетевая модель трансляционно инвариантна.

Взаимные корреляции между флуктуациями остатков можно записать в виде суммы по N-1 ненулевым модам как

$<\Delta R_{i}\cdot \Delta R_{j}>={\frac {3k_{B}T}{\gamma }}[U\Lambda ^{-1}U^{T}]_{ij}={\frac {3k_{B}T}{\gamma }}\sum _{k=1}^{N-1}\lambda _{k}^{-1}[u_{k}u_{k}^{T}]_{ij}$

Отсюда следует, что [ ΔR _i · ΔR _j ] вклад отдельной моды выражается как

$[\Delta R_{i}\cdot \Delta R_{j}]_{k}={\frac {3k_{B}T}{\gamma }}\lambda _{k}^{-1}[u_{k}]_{i}[u_{k}]_{j}$

[ uk _] где _i — й элемент uk _{i -} .

Влияние локальной плотности упаковки

По определению, диагональный элемент матрицы Кирхгофа, Γ _ii , равен степени узла в GNM, который представляет координационное число соответствующего остатка. Это число является мерой локальной плотности упаковки вокруг данного остатка. Влияние локальной плотности упаковки можно оценить путем разложения Γ в ряд ⁻¹ матрица. Γ можно записать как сумму двух матриц Γ = D + O , содержащих диагональные элементы и недиагональные элементы Γ .

С ⁻¹ = ( Д + О ) ⁻¹ = [ Д ( Я + Д ⁻¹ О ) ] ⁻¹ = ( Я + Д ⁻¹ О ) ⁻¹ Д ⁻¹ = ( Я - Д ⁻¹ О +...) Д ⁻¹ = Д ⁻¹ - Д ⁻¹ Д О ⁻¹ + ...

Это выражение показывает, что локальная плотность упаковки вносит существенный вклад в ожидаемые колебания остатков. Члены, которые следуют за обратной диагональной матрицей, представляют собой вклад позиционных корреляций в ожидаемые колебания.

Приложения ГНМ

Рисунок 3: Пример теоретического предсказания ожидаемых колебаний остатков каталитического домена белка Cdc25B, фосфатазы двойной специфичности цикла клеточного деления. А. Сравнение β-факторов рентгеновской структуры (желтый) и теоретических расчетов (красный). Б. Структура каталитического домена Cdc25B, окрашенная в соответствии с теоретической подвижностью регионов. Ожидается, что светло-голубые области, например, самая верхняя альфа-спираль рядом с каталитическим сайтом этого белка, будут более подвижными, чем остальная часть домена. C. Карта взаимной корреляции, т.е. нормализованные < ΔR _i · ΔR _j значения >. Области красного цвета соответствуют коллективным движениям остатков, а области синего цвета соответствуют некоррелированным движениям. Результаты извлекаются с сервера iGNM. Идентификатор PDB Cdc25B — 1QB0.

Колебания равновесия

Равновесные колебания биологических молекул можно измерить экспериментально. В рентгеновской кристаллографии B-фактор (также называемый фактором Дебая-Валлера или температурным фактором) каждого атома является мерой его среднеквадратичного отклонения вблизи положения равновесия в собственной структуре. В экспериментах ЯМР эту меру можно получить путем расчета среднеквадратических различий между различными моделями.Во многих приложениях и публикациях, включая оригинальные статьи, было показано, что ожидаемые флуктуации остатков, полученные с помощью GNM, хорошо согласуются с экспериментально измеренными флуктуациями собственного состояния. Например, связь между B-факторами и ожидаемыми колебаниями остатков, полученными из GNM, следующая:

$B_{i}={\frac {8\pi ^{2}}{3}}<\Delta R_{i}\cdot \Delta R_{i}>={\frac {8\pi ^{2}k_{B}T}{\gamma }}(\Gamma ^{-1})_{ii}$

На рисунке 3 показан пример расчета GNM для каталитического домена белка Cdc25B, цикла деления клеток фосфатазы двойной специфичности .

Рисунок 4: Медленные режимы, полученные в результате расчетов GNM, изображены на каталитическом домене Cdc2B. А. График самого медленного режима. Б. Отображение амплитуды движения в самом медленном режиме на структуру белка. Альфа-спираль вблизи каталитического сайта этого домена является наиболее подвижным участком белка в самом медленном режиме. Ожидаемые значения колебаний также были самыми высокими в этом регионе, как показано на рисунке 3. Результаты получены с сервера iGNM. Идентификатор PDB Cdc25B — 1QB0.

Физический смысл медленных и быстрых режимов

Диагонализация матрицы Кирхгофа разлагает конформационные движения на спектр коллективных мод. Ожидаемые значения флуктуаций и взаимных корреляций получаются из линейных комбинаций флуктуаций вдоль этих нормальных мод. Вклад каждой моды масштабируется пропорционально частоте этой моды. Следовательно, медленные (низкочастотные) моды вносят наибольший вклад в ожидаемые флуктуации. Показано, что среди нескольких самых медленных режимов движения являются коллективными и глобальными и потенциально имеют отношение к функциональности биомолекул. С другой стороны, быстрые (высокочастотные) моды описывают некоррелированные движения, не вызывающие заметных изменений в структуре. Методы, основанные на ГНМ, не обеспечивают реальной динамики, а лишь аппроксимацию, основанную на сочетании и интерполяции нормальных режимов. Их применимость сильно зависит от того, насколько коллективным является движение.

Другие специальные приложения

Существует несколько основных областей, в которых модель гауссовой сети и другие модели эластичных сетей оказались полезными. К ним относятся:

• Сетевая модель на основе пружинных шариков . В сетевой модели на основе пружинных шариков пружины и шарики используются в качестве компонентов в сшитой сети. Пружины сшиты для представления механического поведения материала и модели молекулярной динамики моста (MD) и модели конечных элементов (FE) (см. Рисунок 5). Шарики представляют собой материальную массу кластерных связей. Каждая пружина используется для обозначения группы полимерных цепей, а не части одной полимерной цепи. Это упрощение позволяет объединить различные модели в разных масштабах и значительно повышает эффективность моделирования. На каждой итерации моделирования силы пружин прикладываются к узлам в центре буртиков и рассчитываются уравновешенные узловые перемещения по всей системе. В отличие от традиционного метода КЭ для получения напряжений и деформаций, модель «пружина-буртик» обеспечивает перемещения узлов и силы в пружинах. Эквивалентную деформацию и энергию деформации модели сети на основе пружины-шарика можно определить и рассчитать с использованием смещений узлов и характеристик пружины. Кроме того, результаты сетевой модели можно масштабировать для получения структурной реакции на макроуровне с использованием анализа конечных элементов.
• Разложение гибких/жестких областей и доменов белков
• Характеристика функциональных движений и функционально важных участков/остатков белков, ферментов и крупных макромолекулярных ансамблей.
• Уточнение и динамика структурных данных с низким разрешением, например, криоэлектронная микроскопия.
• Молекулярная замена для решения рентгеновских структур , когда произошло конформационное изменение по отношению к известной структуре.
• Интеграция с атомистическими моделями и симуляциями
• Исследование путей и кинетики складывания/раскладывания.
• Аннотация функционального значения молекулярной эволюции

Веб-серверы

На практике можно выполнить два вида вычислений.Первый тип (GNM как таковой) использует матрицу Кирхгофа . Второй тип (более конкретно называемый либо моделью эластичной сети, либо моделью анизотропной сети) использует матрицу Гессе, связанную с соответствующим набором гармонических пружин. Оба типа моделей можно использовать онлайн, используя следующие серверы.

ГНМ-серверы

• iGNM: база данных функциональных движений белков на основе GNM http://ignm.ccbb.pitt.edu
• oGNM: Онлайн-расчет структурной динамики с использованием GNM https://web.archive.org/web/20070516042756/http://ignm.ccbb.pitt.edu/GNM_Online_Calculation.htm

Серверы ENM/ANM

• модели анизотропной сети Веб-сервер http://www.ccbb.pitt.edu/anm
• elNemo: веб-интерфейс к модели эластичной сети http://www.sciences.univ-nantes.fr/elnemo/
• AD-ENM: Анализ динамики модели эластичной сети http://enm.lobos.nih.gov/
• WEBnm@: Веб-сервер для анализа белков в нормальном режиме http://apps.cbu.uib.no/webnma/home

Другие соответствующие серверы

• ProDy: интерфейс прикладного программирования (API) на Python, который объединяет анализы GNM и ANM, а также несколько инструментов анализа молекулярной структуры и последовательностей, а также инструментов визуализации: http://prody.csb.pitt.edu
• HingeProt: алгоритм прогнозирования белковых шарниров с использованием моделей эластичных сетей http://www.prc.boun.edu.tr/appserv/prc/hingeprot/ или http://bioinfo3d.cs.tau.ac.il/HingeProt/ шарнирпрот.html
• DNABindProt: сервер для определения потенциальных сайтов связывания белков с ДНК http://www.prc.boun.edu.tr/appserv/prc/dnabindprot/
• MolMovDB: База данных макромолекулярных движений: http://www.molmovdb.org/

См. также

• Гауссово распределение
• Гармонический осциллятор
• Закон Гука
• Молекулярная динамика
• Обычный режим
• Анализ главных компонентов
• Динамика белка
• Эластичность резины
• Статистическая механика

Ссылки

Первоисточники

• Бахар, И.; Атилган, Арканзас; Эрман, Б. (1997). «Прямая оценка тепловых колебаний белка с использованием гармонического потенциала одного параметра». Складывание и дизайн . 2 (3): 173–181. дои : 10.1016/s1359-0278(97)00024-2 . ПМИД   9218955 .
• Халилоглу, Т. Бахар; Эрман, Б. (1997). «Гауссова динамика свернутых белков». Физ. Преподобный Летт . 79 (16): 3090–3093. Бибкод : 1997PhRvL..79.3090H . дои : 10.1103/physrevlett.79.3090 .
• Цуй К, Бахар I (2006). Анализ в нормальном режиме: теория и приложения к биологическим и химическим системам, Chapman & Hall/CRC, Лондон, Великобритания.