Занятой бобр
В этой статье есть несколько проблем. Пожалуйста, помогите улучшить его или обсудите эти проблемы на странице обсуждения . ( Узнайте, как и когда удалять эти шаблонные сообщения )
|

В теоретической информатике игра занятого бобра направлена на поиск завершающей программы заданного размера, которая (в зависимости от определения) либо производит максимально возможный результат, либо выполняет наибольшее количество шагов. [2] Поскольку легко придумать программу с бесконечным циклом, производящую бесконечный вывод или работающую бесконечное время, такие программы исключаются из игры. [2] В отличие от традиционных языков программирования, программы, используемые в игре, представляют собой машины Тьюринга с n состояниями . [2] одна из первых математических моделей вычислений. [3]
Машины Тьюринга состоят из бесконечной ленты и конечного набора состояний, которые служат «исходным кодом» программы. Получение наибольшего результата определяется как запись на ленту наибольшего количества единиц, что также называется достижением наивысшего балла, а работа в течение самого длительного времени определяется как выполнение наибольшего количества шагов для остановки. [4] Игра занятого бобра с n состояниями состоит в поиске машины Тьюринга, которая работает дольше всех или имеет самые высокие результаты, которая имеет n состояний и в конечном итоге останавливается. [2] Предполагается, что такие машины запускаются с пустой ленты, и предполагается, что лента содержит только нули и единицы (двоичная машина Тьюринга). [2] Игрок должен придумать набор переходов между состояниями, стремясь к наибольшему количеству очков или максимальному времени работы, одновременно гарантируя, что машина в конечном итоге остановится.
занятой n-й бобер , BB- n или просто «занятый бобер» — это машина Тьюринга, которая выигрывает игру занятого бобра с n состояниями. [5] В зависимости от определения, она либо набирает наивысший балл, либо работает дольше всех других возможных конкурирующих машин Тьюринга с n -состояниями. Функциями, определяющими наивысший балл или наибольшее время работы занятых бобров с n -состояниями по каждому определению, являются Σ(n) и S(n) соответственно. [4]
Определить время работы или счет n- го занятого бобра невозможно подсчитать . [4] Фактически, обе функции Σ(n) и S(n) со временем становятся больше любой вычислимой функции. [4] Это имеет значение для теории вычислимости , проблемы остановки и теории сложности . [6] Эта концепция была впервые представлена Тибором Радо в его статье 1962 года «О невычислимых функциях». [4] Один из наиболее интересных аспектов игры с занятым бобром заключается в том, что если бы было возможно вычислить функции Σ(n) и S(n) для всех n , то это разрешило бы все математические гипотезы, которые можно закодировать как «делает ли это Машина Тьюринга остановится или нет». [5] Например, машина Тьюринга с 27 состояниями могла бы проверить гипотезу Гольдбаха для каждого числа и остановиться на контрпримере: если бы эта машина не остановилась после выполнения S(27) шагов, то она должна работать вечно, разрешая гипотезу. [5] Многие другие проблемы, включая гипотезу Римана (744 состояния) и непротиворечивость теории множеств ZF только бесконечное ( счетное ) число случаев. (748 состояний), могут быть выражены в аналогичной форме, где необходимо проверить [5]
Техническое определение
[ редактировать ]Игра n занятого бобра с состояниями (или BB -n игра ), представленная в статье Тибора Радо 1962 года, включает в себя класс машин Тьюринга , каждый член которых должен соответствовать следующим конструктивным спецификациям:
- Машина имеет n «рабочих» состояний плюс состояние «Останов», где n — целое положительное число, и одно из n состояний считается стартовым. (Обычно состояния обозначаются цифрами 1, 2, ..., n , причем состояние 1 является начальным состоянием, или A , B , C , ..., состояние A является начальным состоянием.)
- Машина использует одну двустороннюю бесконечную (или неограниченную) ленту.
- Алфавит ленты — {0, 1}, где 0 служит пустым символом.
- машины Функция перехода принимает два входа:
- текущее состояние без остановки,
- символ в текущей ячейке ленты,
- и производит три вывода:
- символ для записи поверх символа в текущей ячейке ленты (это может быть тот же символ, что и перезаписанный символ),
- направление перемещения (влево или вправо; то есть сдвиг к ячейке ленты на одно место влево или вправо от текущей ячейки) и
- состояние перехода (которое может быть состоянием остановки).
«Запуск» машины состоит из запуска в начальном состоянии, где текущей ячейкой ленты является любая ячейка пустой ленты (все 0), а затем повторения функции перехода до тех пор, пока не будет введено состояние «Остановка» (если вообще когда-либо). машины Если и только если машина в конце концов останавливается, то количество единиц, оставшихся на ленте, называется счетом . Таким образом, игра «Занятый бобр» с n состояниями (BB- n ) представляет собой соревнование, в зависимости от определения, чтобы найти такую машину Тьюринга с n состояниями, имеющую максимально возможный результат или время работы.
Связанные функции
[ редактировать ]Функция оценки Σ
[ редактировать ]Функция оценки количественно определяет максимальный балл, который может получить занятой бобр по заданному показателю. Это невычислимая функция . Можно показать, что эта функция растет асимптотически быстрее, чем любая вычислимая функция. [7]
Функция оценки, , определяется так, что Σ( n ) является максимально достижимым баллом (максимальное количество единиц, наконец, на ленте) среди всех останавливающихся 2-символьных машин Тьюринга с n состояниями описанного выше типа при запуске на пустой ленте.
Ясно, что Σ является четко определенной функцией: для каждого n существует не более конечного числа с n машин Тьюринга состояниями, как указано выше, с точностью до изоморфизма, следовательно, не более конечного числа возможных времен работы.
Эта бесконечная последовательность Σ является функцией оценки, и согласно определению, основанному на оценке, любая с n 2-символьная машина Тьюринга M состояниями , для которой σ ( M ) = Σ( n ) (т. е. которая достигает максимального результата), называется занятой бобер. Обратите внимание, что для каждого n существует не менее 4( n − 1)! n - состояние занятых бобров. (Для любого занятого бобра с n состояниями другое получается путем простого изменения направления сдвига при останавливающемся переходе, третье - путем равномерного изменения всех направлений сдвига, а четвертое - путем изменения направления остановки занятого бобра, в котором все заменены местами. Кроме того, перестановка всех состояний, кроме «Старт» и «Остановка», дает машину, которая набирает один и тот же балл. Теоретически может быть более одного вида перехода, ведущего к состоянию остановки, но на практике это было бы расточительно, поскольку существует только одна последовательность состояний. переходы, дающие искомый результат.)
Невычислимость
[ редактировать ]Статья Радо 1962 года доказала, что если — любая вычислимая функция , то Σ( n ) > f ( n ) для всех достаточно больших n , и, следовательно, Σ не является вычислимой функцией. [4]
Более того, это означает, что невозможно решить с помощью общего алгоритма , является ли произвольная машина Тьюринга занятым бобром. (Такой алгоритм не может существовать, потому что его существование позволило бы вычислить Σ, что является доказанной невозможностью. В частности, такой алгоритм можно использовать для построения другого алгоритма, который будет вычислять Σ следующим образом: для любого заданного n каждый из конечное число с n двухсимвольных машин Тьюринга -состояниями будет тестироваться до тех пор, пока не будет найден занятый бобер с n -состояниями; затем эта занятая бобер-машина будет смоделирована для определения ее оценки, которая по определению равна Σ( n ).)
Несмотря на то, что Σ( n ) является невычислимой функцией, существуют некоторые малые n , для которых можно получить ее значения и доказать, что они верны. Нетрудно показать, что Σ(0) = 0, Σ(1) = 1, Σ(2) = 4, и со все большей трудностью можно показать, что Σ(3) = 6, Σ(4) = 13 и Σ(5) = 4098 (последовательность A028444 в OEIS ). Σ( n ) еще не была определена ни для одного случая n > 5, хотя нижние границы были установлены (см. раздел «Известные значения» ниже).
Сложность и недоказуемость Σ
[ редактировать ]Вариант колмогоровской сложности определяется следующим образом: [8] Сложность — это наименьшее количество состояний, необходимое для машины Тьюринга класса BB , числа n которая останавливается на одном блоке из n последовательных единиц на изначально пустой ленте. Соответствующий вариант теоремы Чайтина о неполноте утверждает, что в контексте данной аксиоматической системы для натуральных чисел существует число k такое, что ни одно конкретное число не может иметь сложность, превышающую k , и, следовательно, не существует конкретной верхней границы может быть доказано для Σ( k ) (последнее связано с тем, что «сложность n больше k » была бы доказана, если бы было доказано n > Σ( k ) . Как упоминалось в цитируемой ссылке, для любой аксиоматической системы «обычной математики» наименьшее значение k , для которого это верно, намного меньше 10⇈10 ; следовательно, в контексте обычной математики ни значение, ни верхняя граница Σ(10⇈10) не могут быть доказаны. ( Первая теорема Гёделя о неполноте иллюстрируется этим результатом: в аксиоматической системе обычной математики существует истинное, но недоказуемое предложение вида Σ(10⇈10) = n , и существует бесконечно много истинных, но недоказуемых предложений вида Σ(10⇈10) < n .)
Функция максимального смещения S
[ редактировать ]В дополнение к функции Σ Радо [1962] ввел еще одну экстремальную функцию для машин Тьюринга, функцию максимальных сдвигов , S определенную следующим образом: [4]
- s ( M ) = количество сдвигов, которые делает перед остановкой, для любого M ∈ En M ,
- S ( п ) знак равно Макс { s ( M ) | M ∈ En 2 } = наибольшее число сдвигов, сделанных любой останавливающейся -символьной машиной Тьюринга с n состояниями.
Поскольку обычные машины Тьюринга должны иметь сдвиг при каждом переходе или «шаге» (включая любой переход в состояние остановки), функция максимальных сдвигов в то же время является функцией максимальных шагов.
Радо показал, что S невычислима по той же причине, по которой невычислима Σ: она растет быстрее, чем любая вычислимая функция. Он доказал это, просто заметив, что для каждого S n ( n ) ≥ Σ( n ). Каждый сдвиг может записать на ленту 0 или 1, тогда как Σ подсчитывает подмножество сдвигов, на которых записана 1, а именно те, которые не были перезаписаны к моменту остановки машины Тьюринга; следовательно, S растет по крайней мере так же быстро, как Σ, которая, как уже было доказано, растет быстрее, чем любая вычислимая функция. [4]
Следующая связь между Σ и S была использована Лином и Радо [ Компьютерные исследования проблем машины Тьюринга , 1965] для доказательства того, что Σ(3) = 6: Для заданного n , если S ( n известно ), то все n -состояния Машины Тьюринга (в принципе) могут работать до S ( n ) шагов, после чего любая машина, которая еще не остановилась, никогда не остановится. В этот момент, наблюдая, какие машины остановились с наибольшим количеством единиц на ленте (т. е. занятые бобры), можно получить из их лент значение Σ( n ). Подход, использованный Лином и Радо для случая n = 3, заключался в предположении, что S (3) = 21, а затем в моделировании всех существенно разных автоматов с тремя состояниями за 21 шаг. Анализируя поведение машин, которые не остановились в течение 21 шага, им удалось показать, что ни одна из этих машин никогда не остановится, тем самым доказав гипотезу о том, что S (3) = 21, и определив, что Σ(3) = 6 по формуле только что описанную процедуру. [ нужна полная цитата ]
В 2016 году Адам Йедидиа и Скотт Ааронсон получили первую (явную) верхнюю оценку минимума n, для которого S( n ) недоказуемо в ZFC . Для этого они построили штат 7910. [9] Машина Тьюринга, поведение которой не может быть доказано на основе обычных аксиом теории множеств ( теория множеств Цермело–Френкеля с аксиомой выбора ), при разумных гипотезах непротиворечивости ( стационарное свойство Рамсея ). [10] [11] Затем Стефан О'Рир сократил его до 1919 штатов, устранив зависимость от стационарной собственности Рэмси. [12] [13] а затем в 748 штатов. [6] В июле 2023 года Рибель сократил его до 745 штатов. [14] [15]
Доказательство невычислимости S ( n ) и Σ( n )
[ редактировать ]Предположим, что S ( n ) — вычислимая функция, и пусть EvalS обозначает TM, оценивающую S ( n ). Учитывая ленту с n 1, она создаст S ( n ) 1 на ленте, а затем остановится. Пусть Clean обозначает машину Тьюринга, очищающую последовательность единиц, изначально записанную на ленте. Пусть Double обозначает функцию вычисления машины Тьюринга n + n . Учитывая ленту с n 1, она создаст 2 n на ленте 1, а затем остановится. Создадим композицию Double | ЭвалС | Очистите и пусть n 0 — количество состояний этой машины. Пусть Create_n 0 обозначает машину Тьюринга, создающую n 0 1 на изначально пустой ленте. Эту машину можно сконструировать тривиальным образом так, чтобы она имела n 0 состояний (состояние i записывает 1, перемещает головку вправо и переключается в состояние i + 1, за исключением состояния n 0 , которое останавливается). Обозначим через N сумму n 0 + n 0 .
Обозначим через BadS композицию Create_n 0 | Двойной | ЭвалС | Чистый . Обратите внимание, что эта машина имеет N состояний. Начиная с изначально пустой ленты, он сначала создает последовательность из n 0 1, а затем удваивает ее, создавая последовательность из N 1. Затем BadS создаст на ленте S ( N )1 и, наконец, очистит все единицы, а затем остановится. Но фаза очистки будет продолжаться не менее S ( N ) шагов, поэтому время работы BadS строго больше S ( N ), что противоречит определению функции S ( n ).
Невычислимость Σ( n ) может быть доказана аналогичным образом. В приведенном выше доказательстве необходимо заменить машину EvalS на EvalΣ и Clean на Increment — простой TM, ищущий на ленте первый 0 и заменяющий его 1.
Невычислимость S ( n ) также может быть установлена с помощью проблемы остановки пустой ленты. Проблема остановки пустой ленты — это проблема решения для любой машины Тьюринга, остановится она или нет при запуске на пустой ленте. Проблема остановки пустой ленты эквивалентна стандартной проблеме остановки и поэтому также невычислима. Если бы S ( n ) было вычислимо, то мы могли бы решить проблему остановки пустой ленты, просто запустив любую данную машину Тьюринга с n состояниями для S ( n ) шагов; если оно еще не остановилось, то никогда не остановится. Итак, поскольку проблема остановки пустой ленты невычислима, отсюда следует, что S ( n ) также должно быть невычислимым.
Другие функции
[ редактировать ]Ряд других невычислимых функций можно определить на основе измерения производительности машин Тьюринга другими способами, кроме времени или максимального числа. [16] Например: [16]
- Функция определяется как максимальное количество последовательных чисел, которые останавливающаяся машина Тьюринга может записать на чистую ленту. Другими словами, это наибольшее унарное число, которое машина Тьюринга с n состояниями может записать на ленту.
- Функция определяется как максимальное количество клеток ленты, которые останавливающаяся машина Тьюринга может прочитать (т. е. посетить) перед остановкой. Сюда входит начальный квадрат, но не квадрат, которого машина достигает только после перехода с остановкой (если переход с остановкой отмечен направлением движения), поскольку этот квадрат не влияет на поведение машины. Это максимальная пространственная сложность машины Тьюринга с n состояниями.
Обе эти функции также невычислимы. [16] Это можно показать для отметив, что каждый квадрат ленты, в который машина Тьюринга записывает единицу, она также должна посетить: другими словами, . [16] невычислимость функции можно показать, доказав, например, что : это можно сделать, разработав машину Тьюринга с (3n+3) состояниями, которая имитирует чемпиона пространства с n состояниями, а затем использует ее для записи по крайней мере смежные с лентой. [16] Эти функции находятся в отношении: [16]
Обобщения
[ редактировать ]Аналоги функции сдвига можно просто определить на любом языке программирования, поскольку программы можно описывать битовыми строками и подсчитывать количество шагов программы. [17] Например, игру занятого бобра также можно обобщить до двух измерений, используя машины Тьюринга на двумерных лентах, или до машин Тьюринга, которым разрешено оставаться в одном и том же месте, а также перемещаться влево и вправо. [17] В качестве альтернативы «функция занятого бобра» для различных моделей вычислений может быть определена с колгоморовской сложностью . [17] Это делается путем принятия быть наибольшим целым числом такой, что , где длина самой короткой программы в который выводит : таким образом, является самым большим целым числом программы длиной или меньше может выводить в . [17]
Самая продолжительная машина с 6 состояниями и 2 символами, имеющая дополнительное свойство переворачивать значение ленты на каждом шаге, выдает 6147 единиц после 47 339 970 шагов. [ нужна ссылка ] Итак, для класса Обратной машины Тьюринга (RTM) [18] S РТМ (6) ≥ 47 339 970 и Σ РТМ (6) ≥ 6 147 . Аналогичным образом мы могли бы определить аналог функции Σ для регистровых машин как наибольшее число, которое может присутствовать в любом регистре при остановке для заданного количества инструкций. [ нужна ссылка ]
Разное количество символов
[ редактировать ]Простым обобщением является расширение машин Тьюринга с m символами вместо 2 (0 и 1). [17] Например, троичная машина Тьюринга с m = 3 символами будет иметь символы 0, 1 и 2. Обобщение машин Тьюринга с n состояниями и m символами определяет следующие обобщенные функции занятого бобра :
- Σ( n , m ): наибольшее количество ненулевых символов, которые можно напечатать машиной с n- состоянием и m -символом, запущенной на изначально пустой ленте перед остановкой, [ нужна ссылка ] и
- S ( n , m ): наибольшее количество шагов, выполненных машиной с n -состоянием и m -символом, начатой на изначально пустой ленте перед остановкой. [17]
Например, самая долго работающая трехсимвольная машина с тремя состояниями, найденная на данный момент, делает 119 112 334 170 342 540 шагов, прежде чем остановиться. [19] [ нужен лучший источник ]
Недетерминированные машины Тьюринга
[ редактировать ]| п | шаги | государства |
|---|---|---|
| 1 | 2 | 2 |
| 2 | 4 | 4 |
| 3 | 6 | 7 |
| 4 | 7 | 11 |
| 5 | 8 | 15 |
| 6 | 7 | 18 |
| 7 | 6 | 18 |
Задачу можно распространить на недетерминированные машины Тьюринга , ища систему с наибольшим количеством состояний во всех ветвях или ветвь с самым длинным числом шагов. [20] Вопрос о том, остановится ли данный NDTM, по-прежнему неразрешим с вычислительной точки зрения, и вычисления, необходимые для поиска занятого бобра NDTM, значительно больше, чем в детерминистическом случае, поскольку существует несколько ветвей, которые необходимо учитывать. Для системы с 2 состояниями и 2 цветами с p случаями или правилами в таблице справа указано максимальное количество шагов до остановки и максимальное количество уникальных состояний, созданных NDTM.
Приложения
[ редактировать ]Открытые математические задачи
[ редактировать ]Помимо создания довольно сложной математической игры , функции занятого бобра Σ(n) и S ( n ) предлагают совершенно новый подход к решению чисто математических задач. Многие открытые проблемы математики теоретически, но не на практике, могут быть решены систематическим способом, учитывая значение S ( n ) для достаточно большого n . [5] [21] Теоретически, значение S(n) кодирует ответ на все математические гипотезы, которые могут быть проверены машиной Тьюринга с количеством состояний, меньшим или равным n . [6]
Рассмотрим любой гипотеза : любая гипотеза, которую можно опровергнуть с помощью контрпримера в счетном числе случаев (например, гипотеза Гольдбаха ). Напишите компьютерную программу, которая последовательно проверяет эту гипотезу на предмет увеличения значений. В случае гипотезы Гольдбаха мы последовательно рассматривали бы каждое четное число ≥ 4 и проверяли, является ли оно суммой двух простых чисел. Предположим, что эта программа моделируется на машине Тьюринга с n состояниями. Если он находит контрпример (четное число ≥ 4, которое не является суммой двух простых чисел в нашем примере), он останавливается и указывает на это. Однако если гипотеза верна, то наша программа никогда не остановится. (Эта программа останавливается, только если находит контрпример.) [6]
Теперь эта программа моделируется машиной Тьюринга с n состояниями, поэтому, если мы знаем S ( n ), мы можем решить (за конечный промежуток времени), остановится ли она когда-либо или нет, просто запустив машину на такое количество шагов. И если после S ( n ) шагов машина не остановится, мы знаем, что она никогда не остановится и, следовательно, не существует контрпримеров к данной гипотезе (т. е. не существует четных чисел, не являющихся суммой двух простых чисел). Это докажет, что гипотеза верна. [6] Таким образом, конкретные значения (или верхние границы) для S ( n ) теоретически могут использоваться для систематического решения многих открытых проблем математики. [6]
Однако текущие результаты по проблеме занятого бобра предполагают, что это непрактично по двум причинам: [ нужна ссылка ]
- Чрезвычайно сложно доказать значения функции занятого бобра (и функции максимального сдвига). Каждое известное точное значение S ( n ) было доказано путем перечисления каждой машины Тьюринга с n состояниями и проверки того, останавливается ли каждая из них. пришлось бы вычислить S ( n ) каким-то менее прямым методом. Чтобы это действительно было полезно, [ нужна ссылка ]
- Значения S(n) и других занятых функций бобра очень быстро становятся очень большими. Хотя значение S(5) составляет всего около 47 миллионов, значение S(6) превышает 10⇈15, что равно со стеком 15 десяток. [17] [ нужен лучший источник ] Это число имеет 10⇈14 цифр, и его нецелесообразно использовать в вычислениях. Значение S(27), которое представляет собой число шагов, которые должна выполнить текущая программа для гипотезы Гольдбаха , чтобы дать окончательный ответ, непостижимо огромно, и его невозможно даже отдаленно записать, не говоря уже о том, чтобы запустить машину для , в наблюдаемой Вселенной. [5]
Проверка непротиворечивости теорий
[ редактировать ]Еще одним свойством S(n) является то, что ни одна арифметически обоснованная, вычислимо аксиоматизированная теория не может доказать все значения функции. В частности, при наличии вычислимой и арифметически обоснованной теории , есть номер такой, что для всех , нет заявления вида может быть доказано в . [6] Это означает, что для каждой теории существует конкретное наибольшее значение S(n), которое она может доказать. Это верно, поскольку для каждого такого , машина Тьюринга с может быть спроектирован так, чтобы перечислять все возможные доказательства в . [6] Если теория противоречива, то все ложные утверждения доказуемы, и машине Тьюринга можно задать условие остановки тогда и только тогда, когда она найдет доказательство, например, . [6] Любая теория, доказывающая ценность доказывает свою непротиворечивость, нарушая вторую теорему Гёделя о неполноте . [6] Это можно использовать для размещения различных теорий на шкале, например, различных больших кардинальных аксиом в ZFC : если каждая теория присваивается его номер , теории с большими значениями доказать непротиворечивость тех, кто ниже их, помещая все такие теории в счетную бесконечность. [6]
Яркие примеры
[ редактировать ]- Была построена двоичная машина Тьюринга с 745 состояниями, которая останавливается тогда и только тогда, когда ZFC несовместим. [14] [15]
- Была построена машина Тьюринга с 744 состояниями, которая останавливается тогда и только тогда, когда гипотеза Римана ложна. [12] [5]
- Была построена машина Тьюринга с 43 состояниями, которая останавливается тогда и только тогда, когда гипотеза Гольдбаха ложна, а машина с 27 состояниями для этой гипотезы была предложена, но еще не проверена. [12] [5]
- Была построена машина Тьюринга с 15 состояниями, которая останавливается тогда и только тогда, когда следующая гипотеза, сформулированная Полом Эрдешем в 1979 году, неверна: для всех n > 8 существует хотя бы одна цифра 2 в представлении числа 2 по основанию 3. н . [22] [23]
Универсальные машины Тьюринга
[ редактировать ]При исследовании взаимосвязи между универсальностью вычислений и динамическим поведением машин Тьюринга Busy Beaver в 2012 году была выдвинута гипотеза. [24] предполагая, что машины Busy Beaver были естественными кандидатами на универсальность Тьюринга, поскольку они демонстрируют сложные характеристики, известные (1) своей максимальной вычислительной сложностью в пределах ограничений размера, (2) своей способностью выполнять нетривиальные вычисления перед остановкой и (3) сложностью в поиске и проверке этих машин; эти особенности позволяют предположить, что машины Busy Beaver обладают необходимой сложностью для универсальности.
Известные результаты
[ редактировать ]Нижние границы
[ редактировать ]Зеленые машины
[ редактировать ]В 1964 году Милтон Грин разработал нижнюю оценку для варианта функции Занятого Бивера со счетом 1 с, которая была опубликована в материалах симпозиума IEEE 1964 года по теории коммутационных цепей и логическому проектированию. Хайнер Марксен и Юрген Бунтрок описали это как «нетривиальную (не примитивно рекурсивную) нижнюю границу». [25] Эту нижнюю границу можно вычислить, но она слишком сложна, чтобы ее можно было сформулировать как одно выражение в терминах n . [26] Это было сделано с помощью набора машин Тьюринга, каждая из которых демонстрировала нижнюю границу для определенного n . [26] Когда n = 8, метод дает
- .
Напротив, лучшая текущая (по состоянию на 2024 г.) нижняя граница является , где каждый — обозначение Кнута, направленное вверх . [17] Это представляет , возведенная в степень цепочка из 15 десятков, равная . Стоимость вероятно, гораздо больше этого.
В частности, нижняя граница была показана с помощью серии рекурсивных машин Тьюринга, каждая из которых состояла из меньшей машины с двумя дополнительными состояниями, которые неоднократно применяли меньшую машину к входной ленте. [26] Определение ценности конкурента-занятого бобра в N-состоянии на ленте, содержащей те, кто будет (конечная продукция каждой машины равна ее стоимости на , поскольку на пустой ленте их 0), рекурсивные отношения следующие: [26] а
Это приводит к двум формулам для нечетных и четных чисел для расчета нижней границы, заданной N-й машиной: :
- для нечетного N
- даже для N
Нижнюю оценку BB(N) можно также связать с функцией Аккермана . Можно показать, что: [27]
Отношения между функциями занятого бобра
[ редактировать ]Тривиально, S(n) ≥ Σ(n), потому что машина, записывающая Σ(n) единиц, должна сделать для этого как минимум Σ(n) шагов. [27] Можно дать ряд верхних оценок времени S(n) с количеством единиц Σ(n):
Определив num(n) как максимальное количество единиц, которые машина Тьюринга с n состояниями может выводить непрерывно, а не в любой позиции (наибольшее унарное число, которое она может вывести), можно показать: [27]
- (Бен-Амрам и др., 1996 г.) [16] )
Бен-Амрам и Петерсен, 2002, также дают асимптотически улучшенную оценку S(n). [ нужна полная цитата ] Существует константа c такая, что для всех n ≥ 2 :
имеет тенденцию быть близко к квадрату , а ведь многие машины дают меньше . [ нужна ссылка ]
Точные значения и нижние границы
[ редактировать ]В следующей таблице перечислены точные значения и некоторые известные нижние оценки для S ( n ), Σ ( n ) и некоторых других занятых функций бобра. В этой таблице используются двухсимвольные машины Тьюринга. Записи отмечены как "?" по крайней мере такого же размера, как и другие записи слева (поскольку все автоматы с n состояниями также являются (n + 1) конечными автоматами) и не больше, чем записи над ними (потому что S(n) ≥ space(n) ≥ Σ( n) ≥ num(n)).
| Функция | 2-государственный | 3-государственный | 4-штатный | 5-штат | 6-штат |
|---|---|---|---|---|---|
| С(н) | 6 ( [6] ) | 21 ( [6] ) | 107 ( [6] ) | 47 176 870 ( [3] ) | > 10⇈15 ( [17] ) |
| пробел (н) | 4 ( [27] ) | 7 ( [27] ) | 16 ( [27] ) | ≥ 12 289 ( [27] ) | ? |
| С(н) | 4 ( [27] ) | 6 ( [27] ) | 13 ( [27] ) | ≥ 4098 ( [27] ) | > 10⇈15 ( [28] ) |
| ли | 4 ( [27] ) | 6 ( [27] ) | 12 ( [27] ) | ? | ? |
Занятой бобр с 5 состояниями был открыт Хайнером Марксеном и Юргеном Бунтроком в 1989 году, но оказался пятым занятым бобром-победителем — стилизованным под BB(5) — только в 2024 году с использованием доказательства в Coq . [29] [30]
Список занятых бобров
[ редактировать ]
Диаграмма сжата, поэтому показаны только этапы замены ленты. Зеленые и желтые треугольники обозначают области, в которых машина Тьюринга курсирует взад и вперед; затраченное время пропорционально площадям этих цветных треугольников. Нижний ряд представляет собой фрагмент ленты и головки чтения/записи после остановки.
Это таблицы правил для машин Тьюринга, которые генерируют Σ(1) и S (1), Σ(2) и S (2), Σ(3) (но не S (3)), Σ(4) и S. (4), Σ(5) и S (5), а также наиболее известную нижнюю оценку для Σ(6) и S (6).
В таблицах столбцы представляют текущее состояние, а строки представляют текущий символ, считанный с ленты. Каждая запись таблицы представляет собой строку из трех символов, указывающую символ для записи на ленту, направление перемещения и новое состояние (именно в этом порядке). Состояние остановки отображается как H .
Каждая машина начинается в состоянии A с бесконечной ленты, содержащей все 0. Таким образом, начальный символ, считанный с ленты, равен 0.
позиции Ключ результата: (начинается с подчеркнутой позиции , заканчивается в подчеркнутой )
Занятый бобр с 1 состоянием и 2 символами А 0 1р ч 1 (не используется)
Результат: 0 0 1 0 0 (1 шаг, всего одна «1»)
Занятый бобр с 2 состояниями и 2 символами [ нужна ссылка ] А Б 0 1Р Б 1л А 1 1л Б 1р ч
Результат: 0 0 1 1 1 1 0 0 (6 шагов, всего четыре единицы)

Результат: 0 0 1 1 1 1 1 1 0 0 (14 шагов, всего шесть единиц).
предыдущих машин, эта занята только для Σ, но не для S. В отличие от ( С (3) = 21.)

Занятый бобр с 4 состояниями и 2 символами А Б С Д 0 1Р Б 1л А 1р ч 1р д 1 1л Б 0Л С 1л д 0Р А
Результат: 0 0 1 0 1 1 1 1 1 1 1 1 1 1 1 1 0 0 (107 шагов, всего тринадцать единиц)
Занятый бобер с 5 состояниями и 2 символами А Б С Д И 0 1Р Б 1р С 1р д 1л А 1р ч 1 1л С 1Р Б 0Л Э 1л д 0Л А
Результат: 4098 «1» с 8191 «0», разбросанными по 47 176 870 шагам.
Обратите внимание на изображение справа, насколько это решение качественно похоже на эволюцию некоторых клеточных автоматов .
текущий лучший претендент на 6 штатов и 2 символа [19] [28] А Б С Д И Ф 0 1Р Б 1р С 1л С 0Л Э 1л Ф 0Р С 1 0Л Д 0Р Ф 1л А 1р ч 0Р Б 0Р Э
Результат: 1 0 1 1 1 ... 1 1 1 («10» с последующими более чем 10↑↑15 последовательными «1» за более чем 10↑↑15 шагов, где 10↑↑15=10 10 . . 10 , показательная башня из 15 десятков).
Визуализации
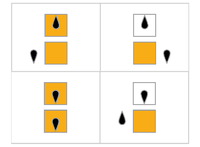
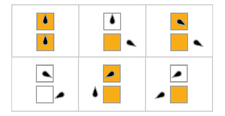
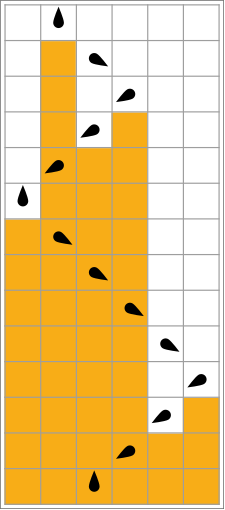
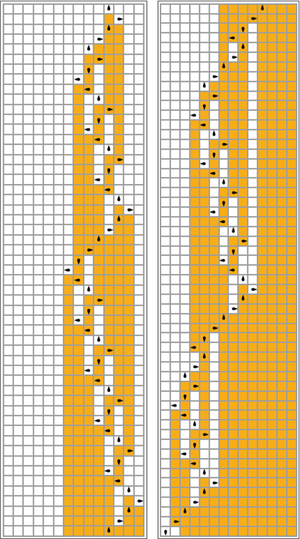
[ редактировать ]В следующей таблице правила для каждого занятого бобра (максимизирующего Σ) представлены визуально: оранжевые квадраты соответствуют цифре «1» на ленте, а белые соответствуют «0». Положение головы обозначено черным овалом, а ориентация головы представляет состояние. Отдельные ленты раскладываются горизонтально, с течением времени сверху вниз. Состояние остановки представлено правилом, которое отображает одно состояние само на себя (голова не двигается).
См. также
[ редактировать ]Примечания
[ редактировать ]- ^ «Вызов занятого бобра: история # пространственно-временных диаграмм» . bbchallenge.org . Проверено 9 июля 2024 г.
- ^ Jump up to: Перейти обратно: а б с д и Вайсштейн, Эрик В. «Занятой бобер» . Вольфрам Математический мир . Проверено 21 ноября 2023 г.
- ^ Jump up to: Перейти обратно: а б Брубейкер, Бен (2 июля 2024 г.). «Математики-любители нашли пятую машину Тьюринга «занятого бобра»» . Журнал Кванта . Проверено 03 июля 2024 г.
- ^ Jump up to: Перейти обратно: а б с д и ж г час Радо, Тибор (май 1962 г.). «О невычислимых функциях» (PDF) . Технический журнал Bell System . 41 (3): 877–884. дои : 10.1002/j.1538-7305.1962.tb00480.x .
- ^ Jump up to: Перейти обратно: а б с д и ж г час Павлус, Джон (10 декабря 2020 г.). «Как самые медленные компьютерные программы выявляют фундаментальные ограничения математики» . Журнал Кванта . Проверено 11 декабря 2020 г.
- ^ Jump up to: Перейти обратно: а б с д и ж г час я дж к л м н Ааронсон, Скотт (29 сентября 2020 г.). «Оживленный бобровый рубеж» . Новости СИГАКТ . 51 (3): 32–54. дои : 10.1145/3427361.3427369 . ISSN 0163-5700 . PDF доступен у автора.
- ^ Чайтин (1987)
- ^ Булос, Берджесс и Джеффри, 2007. «Вычислимость и логика»
- ^ Адам Едидиа и Скотт Ааронсон (май 2016 г.). Относительно небольшая машина Тьюринга, поведение которой не зависит от теории множеств (технический отчет). Массачусетский технологический институт. arXiv : 1605.04343 . Бибкод : 2016arXiv160504343Y .
- ^ Арон, Джейкоб. «Эта машина Тьюринга должна работать вечно, если математика не ошибается» . НовыйУченый . Проверено 25 сентября 2016 г.
- ↑ Версия от 3 мая содержала 7918 состояний: «8000-е число Busy Beaver ускользает от теории множеств ZF» . Shtetl-Оптимизированный блог . 03 мая 2016 г. Проверено 25 сентября 2016 г.
- ^ Jump up to: Перейти обратно: а б с «Три объявления» . Shtetl-Оптимизированный блог . 03 мая 2016 г. Проверено 27 апреля 2018 г.
- ^ «GitHub — sorear/metamath-turing-machines: счетчики доказательства метаматематики и другие вещи» . Гитхаб . 13 февраля 2019 г.
- ^ Jump up to: Перейти обратно: а б «Жизнь, ведение блога и функция Busy Beaver продолжаются» . 05.07.2023 . Проверено 27 августа 2023 г.
- ^ Jump up to: Перейти обратно: а б «Неразрешимость BB (748)» (PDF) . Проверено 27 августа 2023 г.
- ^ Jump up to: Перейти обратно: а б с д и ж г Бен-Амрам, AM; Юльстрем, бакалавр; Цвик, У. (1 августа 1996 г.). «Заметка о занятых бобрах и других существах» . Теория математических систем . 29 (4): 375–386. дои : 10.1007/BF01192693 . ISSN 1433-0490 .
- ^ Jump up to: Перейти обратно: а б с д и ж г час я Ааронсон, Скотт (2 июля 2024 г.). «Теперь известно, что BusyBeaver(5) равен 47 176 870» . Shtetl-Оптимизированный . Проверено 4 июля 2024 г.
- ^ «Обратная машина Тьюринга» . skelet.ludost.net . Проверено 10 февраля 2022 г.
- ^ Jump up to: Перейти обратно: а б Паскаля Мишеля На странице соревнований Busy Beaver перечислены лучшие известные претенденты.
- ^ Jump up to: Перейти обратно: а б Вольфрам, Стивен (4 февраля 2021 г.). «Многосторонние машины Тьюринга» . www.wolframphysicals.org .
- ^ Чайтин, Грегори Дж . (1987). «Вычисление функции занятого бобра» (PDF) . В Прикрытии, ТМ; Гопинатх, Б. (ред.). Открытые проблемы коммуникации и вычислений . Спрингер. стр. 108–112. ISBN 978-0-387-96621-2 . Архивировано из оригинала (PDF) 30 декабря 2017 г. Проверено 7 июля 2022 г.
- ^ Тристан Стерин и Дэмиен Вудс (июль 2021 г.). О сложности знания занятого бобра значений ВВ(15) и ВВ(5,4) (Технический отчет). Университет Мейнут. arXiv : 2107.12475 .
- ^ Эрдыш, Пол (1979). «Некоторые нетрадиционные задачи теории чисел» . Математика. Маг. 52 (2): 67–70. дои : 10.1080/0025570X.1979.11976756 . JSTOR 2689842 .
- ^ Зенил, Гектор (2012). «О динамическом качественном поведении универсальных вычислений» . Сложные системы . 20 (3): 265–277. ISSN 0891-2513 . PDF доступен у издателя.
- ^ Брэди, Аллен Х. (март 1998 г.). «Хайнер Марксен и Юрген Бунтрок. Нападение на занятого бобра 5. Бюллетень Европейской ассоциации теоретической информатики, № 40 (февраль 1990 г.), стр. 247–251. - Паскаль Мишель. Конкуренция занятого бобра и проблемы, подобные Коллатцу. Архив математической логики, том 32 (1993), стр. 351–367» . Журнал символической логики . 63 (1): 331–332. дои : 10.2307/2586607 . ISSN 0022-4812 . Бесплатная HTML-версия от автора
- ^ Jump up to: Перейти обратно: а б с д Грин, Милтон В. (11 ноября 1964 г.). «Нижняя граница сигма-функции RADO для двоичных машин Тьюринга» . Труды Пятого ежегодного симпозиума по теории переключающих цепей и логическому проектированию 1964 года . СВКТ '64. США: Компьютерное общество IEEE: 91–94. дои : 10.1109/SWCT.1964.3 .
- ^ Jump up to: Перейти обратно: а б с д и ж г час я дж к л м н тот п д Бен-Амрам, AM; Петерсен, Х. (1 февраля 2002 г.). «Улучшенные границы для функций, связанных с занятыми бобрами» . Теория вычислительных систем . 35 (1): 1–11. дои : 10.1007/s00224-001-1052-0 . ISSN 1433-0490 .
- ^ Jump up to: Перейти обратно: а б Лигоцки, Шон (21 июня 2022 г.). «ВВ(6, 2) > 10↑↑15» . слигоцкий . Проверено 4 июля 2024 г.
- ^ «[2 июля 2024 г.] Мы доказали, что «BB(5) = 47 176 870» « . Вызов занятого бобра . 2 июля 2024 г. Проверено 2 июля 2024 г.
- ^ «Вызов занятого бобра» . bbchallenge.org . Проверено 2 июля 2024 г.
- ^ Шэнь Линь (1963). Компьютерные исследования задач машины Тьюринга (кандидатская диссертация). Университет штата Огайо .
- ^ Линь, Шен; Радо, Тибор (апрель 1965 г.). «Компьютерные исследования проблем машины Тьюринга» . Журнал АКМ . 12 (2): 196–212. дои : 10.1145/321264.321270 . S2CID 17789208 .
Ссылки
[ редактировать ]- Радо, Тибор (май 1962 г.). «О невычислимых функциях» (PDF) . Технический журнал Bell System . 41 (3): 877–884. дои : 10.1002/j.1538-7305.1962.tb00480.x .
- Именно здесь Радо впервые сформулировал проблему занятого бобра и доказал, что она невычислима и растет быстрее, чем любая вычислимая функция.
- Линь, Шен; Радо, Тибор (апрель 1965 г.). «Компьютерные исследования проблем машины Тьюринга» . Журнал АКМ . 12 (2): 196–212. дои : 10.1145/321264.321270 . S2CID 17789208 .
- Результаты этой статьи уже частично были опубликованы в докторской диссертации Линя в 1963 году под руководством Радо. Лин и Радо доказывают, что Σ(3) = 6 и S (3) = 21, доказывая, что все 2-символьные машины Тьюринга с 3 состояниями, которые не останавливаются в течение 21 шага, никогда не остановятся. (Большинство из них доказываются автоматически с помощью компьютерной программы, однако 40 случаев доказываются при проверке человеком.)
- Брэди, Аллен Х. (апрель 1983 г.). «Определение значения невычислимой функции Радо Σ( k ) для машин Тьюринга с четырьмя состояниями» . Математика вычислений . 40 (162): 647–665. дои : 10.1090/S0025-5718-1983-0689479-6 . JSTOR 2007539 .
- Брейди доказывает, что Σ(4) = 13 и S (4) = 107. Брейди определяет две новые категории для непрерывных 2-символьных машин Тьюринга с 3 состояниями: рождественские елки и счетчики. Он использует компьютерную программу, чтобы доказать, что все машины, кроме 27, которые выполняют более 107 шагов, являются вариантами рождественских елок и счетчиков, которые, как можно доказать, могут работать бесконечно. После личного осмотра самого Брейди доказано, что последние 27 машин (называемых оставшимися) не остановились.
- Махлин, Рона; Стаут, Квентин Ф. (июнь 1990 г.). «Сложное поведение простых машин» . Физика D: Нелинейные явления . 42 (1–3): 85–98. Бибкод : 1990PhyD...42...85M . дои : 10.1016/0167-2789(90)90068-Z . hdl : 2027.42/28528 .
- Махлин и Стаут описывают проблему занятого бобра и многие методы, используемые для поиска занятых бобров (которые они применяют к машинам Тьюринга с 4 состояниями и 2 символами, тем самым проверяя доказательство Брейди). Они предлагают, как оценить вариант вероятности остановки Чайтина (Ω).
- Марксен, Хайнер; Бунтрок, Юрген (февраль 1990 г.). «Атака на занятого бобра 5» . Бюллетень ЕАТКС . 40 : 247–251. Архивировано из оригинала 9 октября 2006 г. Проверено 19 января 2020 г.
- Марксен и Бантрок демонстрируют, что Σ(5) ≥ 4098 и S (5) ≥ 47 176 870 , и подробно описывают метод, который они использовали для поиска этих машин, и доказывают, что многие другие никогда не остановятся.
- Грин, Милтон В. (1964). Нижняя граница сигма-функции Радо для двоичных машин Тьюринга . 1964 г. Труды пятого ежегодного симпозиума по теории переключающих цепей и логическому проектированию . стр. 91–94. дои : 10.1109/SWCT.1964.3 .
- Грин рекурсивно конструирует машины для любого количества состояний и предоставляет рекурсивную функцию, которая вычисляет их оценку (вычисляет σ), тем самым обеспечивая нижнюю оценку Σ. Рост этой функции сравним с ростом функции Аккермана .
- Дьюдни, Александр К. (1984). «Компьютерная ловушка для занятого бобра, самая трудолюбивая машина Тьюринга». Научный американец . 251 (2): 10–17.
- Программы занятых бобров описаны Александром Дьюдни в журнале Scientific American , август 1984 г., стр. 19–23, а также март 1985 г., стр. 23 апреля 1985 г. с. 30 .
- Чайтин, Грегори Дж . (1987). «Вычисление функции занятого бобра» (PDF) . В Прикрытии, ТМ; Гопинатх, Б. (ред.). Открытые проблемы коммуникации и вычислений . Спрингер. стр. 108–112. ISBN 978-0-387-96621-2 . Архивировано из оригинала (PDF) 30 декабря 2017 г. Проверено 7 июля 2022 г.
- Брэди, Аллен Х. (1995). «Игра занятого бобра и смысл жизни». В Херкене, Рольф (ред.). Универсальная машина Тьюринга: обзор полувека (2-е изд.). Вена, Нью-Йорк: Springer-Verlag. стр. 237–254. ISBN 978-3-211-82637-9 .
- При этом Брэди (известный в четырех штатах) описывает некоторую историю зверя и называет его преследование «Игрой занятого бобра». Он описывает другие игры (например, клеточные автоматы и «Игру жизни» Конвея ). Особый интерес представляет «Игра занятого бобра в двух измерениях» (с. 247). С 19 ссылками.
- Бут, Тейлор Л. (1967). Последовательные машины и теория автоматов . Нью-Йорк: Уайли. ISBN 978-0-471-08848-6 .
- См. главу 9 «Машины Тьюринга». Сложная книга, предназначенная для инженеров-электриков и технических специалистов. Обсуждает рекурсию, частичную рекурсию со ссылкой на машины Тьюринга, проблему остановки. Упоминание в Буте приписывает Rado занятого бобра. Бут также определяет проблему занятого бобра Радо в «домашних проблемах» 3, 4, 5, 6 главы 9, с. 396. Задача 3 состоит в том, чтобы «показать, что проблема занятого бобра неразрешима... для всех значений n».
- Бен-Амрам, AM; Юльстрем, бакалавр; Цвик, У. (1996). «Заметка о занятых бобрах и других существах» . Теория математических систем . 29 (4): 375–386. CiteSeerX 10.1.1.75.1297 . дои : 10.1007/BF01192693 . S2CID 30937913 . Архивировано из оригинала 21 июля 2018 г. Проверено 7 июля 2022 г.
- Границы между функциями Σ и S .
- Бен-Амрам, AM; Петерсен, Х. (2002). «Улучшенные границы для функций, связанных с занятыми бобрами». Теория вычислительных систем . 35 : 1–11. CiteSeerX 10.1.1.136.5997 . дои : 10.1007/s00224-001-1052-0 . S2CID 10429773 .
- Улучшенные границы.
- Лафит, Г.; Папазян, К. (июнь 2007 г.). «Ткань маленьких машин Тьюринга». Вычисления и логика в реальном мире, Материалы Третьей конференции по вычислимости в Европе . стр. 219–227. CiteSeerX 10.1.1.104.3021 .
- Эта статья содержит полную классификацию машин Тьюринга с 2 состояниями и 3 символами и, следовательно, доказательство для (2, 3) занятого бобра: Σ(2, 3) = 9 и S(2, 3) = 38.
- Булос, Джордж С.; Берджесс, Джон П.; Джеффри, Ричард С. (2007). Вычислимость и логика (Пятое изд.). Издательство Кембриджского университета. ISBN 978-0-521-87752-7 .
- Кропиц, Павел (2010). Problém Busy Beaver (бакалаврская диссертация) (на словацком языке). Карлов университет в Праге.
- Это описание идей, алгоритмов и их реализации, с описанием экспериментов по изучению машин Тьюринга с 5 и 6 состояниями при параллельном запуске на 31 4-ядерном компьютере и, наконец, лучших результатов для TM с 6 состояниями.
Внешние ссылки
[ редактировать ]- Страница Хайнера Марксена , который вместе с Юргеном Бунтроком нашел вышеупомянутые записи для машины Тьюринга с 5 и 6 состояниями.
- Паскаля Мишеля , который также содержит лучшие результаты и некоторый анализ. Исторический обзор результатов занятых бобров
- Определение класса RTM — обратные машины Тьюринга, простой и сильный подкласс TM.
- « Проблема занятого бобра: атака нового тысячелетия » ( в архиве ) в лаборатории Rensselaer RAIR. В результате этих усилий было обнаружено несколько новых рекордов и установлено несколько значений четверной формализации.
- Дэниела Бриггса веб-сайта Архив и форум для решения проблемы занятого бобра с 5 состояниями и 2 символами на основе Скелета (Георги Георгиева). списка нерегулярных машин
- Лигоцки, Шон (17 июля 2021 г.). «Коллатцоподобное поведение занятых бобров» . слигоцкий . Проверено 12 июля 2022 г.
- Ааронсон, Скотт (1999), Кто может назвать большее число?
- Вайсштейн, Эрик В. «Занятой бобер» . Математический мир .
- Машины Тьюринга Busy Beaver — Компьютерщик , Youtube
- Паскаль Мишель. Конкурс «Занятый бобр»: исторический обзор . 70 страниц. 2017. <hal-00396880v5>