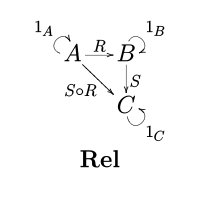
Категория отношений
В математике категория множеств Rel имеет класс как объектов и бинарных отношений как морфизмов .
Морфизм (или стрелка) R : A → B в этой категории — это отношение между множествами A и B , поэтому R ⊆ A × B .
Композиция двух отношений R : A → B и S : B → C определяется формулой
- ( а , c ) ∈ S о R ⇔ для некоторых b ∈ B , ( a , b ) ∈ R и ( b , c ) ∈ S . [1]
Rel также называют «категорией соответствий множеств». [2]
Свойства [ править ]
Категория Rel имеет категорию множеств Set как (широкую) подкатегорию , где стрелка f : X → Y в Set соответствует отношению F ⊆ X × Y , определенному формулой ( x , y ) ∈ F ⇔ f ( x ) = й . [примечание 1] [3]
Морфизм в Rel является отношением, а соответствующий морфизм в категории, противоположной Rel , имеет перевернутые стрелки, поэтому это обратное отношение . Таким образом, Rel содержит свою противоположность и самодвойственен . [4]
Инволюция , представленная обратным соотношением, дает кинжал , чтобы сделать Rel категорией кинжала .
Категория имеет два функтора в себя, заданных функтором hom : бинарное отношение R ⊆ A × B и его транспонирование R Т ⊆ B × A может быть составлено либо как RR Т или как Р Т Р. Первая композиция приводит к отношению на A , а вторая — к B. однородному Поскольку образы этих функторов hom находятся в самом Rel , то в этом случае hom является внутренним функтором hom . Со своим внутренним функтором hom Rel является закрытой категорией и, кроме того, компактной категорией кинжала .
Категория Rel может быть получена из категории Set как категория Клейсли для монады, функтор которой соответствует степенному набору , интерпретируемому как ковариантный функтор.
Возможно, на первый взгляд немного удивителен тот факт, что произведение в Rel задается несвязным объединением [4] : 181 (а не декартово произведение , как в Set ), как и копроизведение .
Rel является моноидально замкнутым , если и моноидальное произведение A ⊗ B , и внутренний hom A ⇒ B определяются декартовым произведением множеств. Это также моноидальная категория , если моноидальное произведение определяется дизъюнктным объединением множеств. [5]
Категория Rel была прототипом алгебраической структуры, названной и Андре Щедровым аллегорией Питером Дж. Фрейдом в 1990 году. [6] Начиная с регулярной категории и функтора F : A → B , они отмечают свойства индуцированного функтора Rel( A,B ) → Rel( FA, FB ). Например, он сохраняет композицию, преобразование и пересечение. Такие свойства затем используются для обеспечения аксиом аллегории.
Отношения как объекты [ править ]
Дэвид Райдхард и Род Берстолл считают, что у Rel есть объекты, которые представляют собой однородные отношения. Например, A — множество, а ⊆ A × A — бинарное отношение на A. R Морфизмы этой категории — это функции между множествами, которые сохраняют отношение: скажем, S ⊆ B × B — второе отношение, а f : A → B — такая функция, что тогда f — морфизм. [7]
Ту же идею выдвигают Адамек, Геррлих и Штрекер, обозначая объекты ( A, R ) и ( B, S ), множество и отношение. [8]
Примечания [ править ]
- ^ Эта категория называется Set Rel от Райдхеарда и Берстолла.
Ссылки [ править ]
- ^ Мак Лейн, С. (1988). Категории для работающего математика (1-е изд.). Спрингер. п. 26. ISBN 0-387-90035-7 .
- ^ Парейгис, Бодо (1970). Категории и функторы . Чистая и прикладная математика. Том. 39. Академическая пресса . п. 6. ISBN 978-0-12-545150-5 .
- ^ Бергман, Джордж (1998). «§7.2 RelSet». Приглашение к общей алгебре и универсальным конструкциям . Генри Хелсон. ISBN 0-9655211-4-1 .
- ↑ Перейти обратно: Перейти обратно: а б Барр, Майкл ; Уэллс, Чарльз (1990). Теория категорий для информатики (PDF) . Прентис Холл. п. 181. ИСБН 978-0131204867 .
- ^ Фонг, Брендан; Давид И Спивак (2019). «Поставка наворотов в симметричных моноидальных категориях». arXiv : 1908.02633 [ мат.CT ].
- ^ Фрейд, Питер Дж .; Щедров, Андре (1990). Категории, Аллегории . Северная Голландия. стр. 79, 196. ISBN. 0-444-70368-3 .
- ^ Райдхард, Дэвид; Берстолл, Род (1988). Вычислительная теория категорий . Прентис-Холл. п. 41. ИСБН 978-0131627369 .
- ^ Адамек, Юрий; Херрлих, Хорст; Стрекер, Джордж Э. (2004) [1990]. «§3.3, пример 2(d)». Абстрактные и конкретные категории (PDF) . Исследовательская группа KatMAT, Бременский университет . п. 22. Архивировано из оригинала (PDF) 11 августа 2022 г.
- Борсо, Фрэнсис (1994). Категории и структуры . Справочник по категорической алгебре. Том. 2. Издательство Кембриджского университета . п. 115. ИСБН 978-0-521-44179-7 .