Идентичность (математика)

В математике тождество равенство — это , связывающее одно математическое выражение A с другим математическим выражением B , такое, что A и B (которые могут содержать некоторые переменные ) дают одно и то же значение для всех значений переменных в определенном диапазоне допустимости. ^[1] Другими словами, A = B является тождеством, если A и B определяют одни и те же функции , а тождество — это равенство между функциями, которые определены по-разному. Например, $(a+b)^{2}=a^{2}+2ab+b^{2}$ и $\cos ^{2}\theta +\sin ^{2}\theta =1$ являются тождествами. ^[1] Идентичность иногда обозначается тройной чертой ≡ $вместо$ = $,$ знака равенства . ^[2] Формально тождество — это универсально определенное равенство.

Общие личности [ править ]

Алгебраические тождества [ править ]

Определенные личности, такие как $a+0=a$ и $a+(-a)=0$ , составляют основу алгебры , ^[3] в то время как другие личности, такие как $(a+b)^{2}=a^{2}+2ab+b^{2}$ и $a^{2}-b^{2}=(a+b)(a-b)$ , может быть полезен при упрощении алгебраических выражений и их расширении. ^[4]

Тригонометрические тождества [ править ]

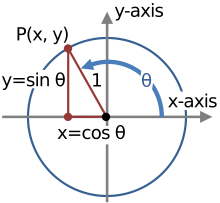
Геометрически тригонометрические тождества — это тождества, включающие в себя определенные функции одного или нескольких углов . ^[5] Они отличаются от тождеств треугольника , которые включают в себя как углы, так и длины сторон треугольника . В этой статье рассматриваются только первые.

Эти тождества полезны всякий раз, когда необходимо упростить выражения, включающие тригонометрические функции. Еще одним важным применением является интегрирование нетригонометрических функций: распространенный метод, который включает сначала использование правила замены тригонометрической функцией , а затем упрощение полученного интеграла с помощью тригонометрического тождества.

Одним из наиболее ярких примеров тригонометрических тождеств является уравнение $\sin ^{2}\theta +\cos ^{2}\theta =1,$ что верно для всех действительных значений $\theta$ . С другой стороны, уравнение

\cos \theta =1

справедливо только для определенных значений $\theta$ , не все. Например, это уравнение верно, когда $\theta =0,$ но ложь, когда $\theta =2$ .

Другая группа тригонометрических тождеств касается так называемых формул сложения и вычитания (например, тождество двойного угла $\sin(2\theta )=2\sin \theta \cos \theta$ , формула сложения для $\tan(x+y)$ ), ^[2] который можно использовать для разбиения выражений больших углов на выражения с меньшими составляющими.

Экспоненциальные тождества [ править ]

Следующие тождества справедливы для всех целочисленных показателей при условии, что основание не равно нулю:

{\begin{aligned}b^{m+n}&=b^{m}\cdot b^{n}\\(b^{m})^{n}&=b^{m\cdot n}\\(b\cdot c)^{n}&=b^{n}\cdot c^{n}\end{aligned}}

В отличие от сложения и умножения, возведение в степень не является коммутативным . Например, 2 + 3 = 3 + 2 = 5 и 2 · 3 = 3 · 2 = 6 , но 2 ³ = 8 тогда как 3 ² = 9 .

Кроме того, в отличие от сложения и умножения, возведение в степень не является ассоциативным . Например, (2 + 3) + 4 = 2 + (3 + 4) = 9 и (2 · 3) · 4 = 2 · (3 · 4) = 24 , но 2 ³ до 4 будет 8 ⁴ (или 4096), тогда как 2 к 3 ⁴ 2 ⁸¹ (или 2 417 851 639 229 258 349 412 352). Если круглые скобки не написаны, по соглашению порядок будет сверху вниз, а не снизу вверх:

b^{p^{q}}:=b^{(p^{q})},

тогда как

(b^{p})^{q}=b^{p\cdot q}.

Логарифмические тождества [ править ]

Несколько важных формул, иногда называемых логарифмическими тождествами или логарифмическими законами , связывают логарифмы друг с другом: ^[а]

Произведение, частное, степень и корень [ править ]

Логарифм произведения — это сумма логарифмов умножаемых чисел; логарифм отношения двух чисел — это разность логарифмов. Логарифм $p-й$ степени числа в $p$ раз больше логарифма самого числа; логарифм $корня p-$ й степени равен логарифму числа, разделенного на $p$ . В следующей таблице перечислены эти личности с примерами. Каждое из тождеств можно получить после подстановки определений логарифмов. $x=b^{\log _{b}x},$ и/или $y=b^{\log _{b}y},$ в левых сторонах.

	Формула	Пример
продукт	$\log _{b}(xy)=\log _{b}(x)+\log _{b}(y)$	$\log _{3}(243)=\log _{3}(9\cdot 27)=\log _{3}(9)+\log _{3}(27)=2+3=5$
частное	$\log _{b}\!\left({\frac {x}{y}}\right)=\log _{b}(x)-\log _{b}(y)$	$\log _{2}(16)=\log _{2}\!\left({\frac {64}{4}}\right)=\log _{2}(64)-\log _{2}(4)=6-2=4$
власть	$\log _{b}(x^{p})=p\log _{b}(x)$	$\log _{2}(64)=\log _{2}(2^{6})=6\log _{2}(2)=6$
корень	$\log _{b}\!{\sqrt[{p}]{x}}={\frac {\log _{b}(x)}{p}}$	$\log _{10}\!{\sqrt {1000}}={\frac {1}{2}}\log _{10}1000={\frac {3}{2}}=1.5$

Смена базы [ править ]

Логарифм log _b ( x ) можно вычислить из логарифмов x и b по произвольному основанию k, используя следующую формулу:

\log _{b}(x)={\frac {\log _{k}(x)}{\log _{k}(b)}}.

Типичные научные калькуляторы вычисляют логарифмы по основаниям 10 и e . ^[6] Логарифмы по любой базе b можно определить, используя любой из этих двух логарифмов по предыдущей формуле:

\log _{b}(x)={\frac {\log _{10}(x)}{\log _{10}(b)}}={\frac {\log _{e}(x)}{\log _{e}(b)}}.

Учитывая число x и его логарифм log _b ( x ) по неизвестной базе b , база определяется следующим образом:

b=x^{\frac {1}{\log _{b}(x)}}.

Гиперболические тождества функций [ править ]

Гиперболические функции удовлетворяют многим тождествам, все из которых по форме аналогичны тригонометрическим тождествам . Фактически, правило Осборна ^[7] утверждает, что можно преобразовать любое тригонометрическое тождество в гиперболическое тождество, полностью расширив его с точки зрения целых степеней синусов и косинусов, заменив синус на sinh и косинус на cosh и изменив знак каждого члена, который содержит произведение четного числа. гиперболических синусов. ^[8]

Функция Гудермана дает прямую связь между тригонометрическими функциями и гиперболическими, не использующими комплексные числа .

Логика и универсальная алгебра [ править ]

Формально тождество — это истинная универсально квантифицированная формула вида $\forall x_{1},\ldots ,x_{n}:s=t,$ где $s$ и $t$ — термины, в которых нет других свободных переменных, кроме $x_{1},\ldots ,x_{n}.$ Префикс квантора $\forall x_{1},\ldots ,x_{n}$ часто остается неявным, когда утверждается, что формула является тождеством. Например, аксиомы моноида часто задаются в виде формул

\forall x,y,z:x*(y*z)=(x*y)*z,\quad \forall x:x*1=x,\quad \forall x:1*x=x,

или, короче,

x*(y*z)=(x*y)*z,\qquad x*1=x,\qquad 1*x=x.

Итак, эти формулы являются тождествами в каждом моноиде. Что касается всякого равенства, то формулы без квантора часто называют уравнениями . Другими словами, тождество — это уравнение, истинное для всех значений переменных. ^[9]^[10]

См. также [ править ]

Ссылки [ править ]

Примечания [ править ]

^ Все утверждения в этом разделе можно найти в Shirali 2002 , Раздел 4, Downing 2003 , p. 275, или Кейт и Бхапкар 2009 , с. Например, 1-1.

Цитаты [ править ]

^ Jump up to: Перейти обратно: ^а ^б «Математические слова: идентичность» . www.mathwords.com . Проверено 1 декабря 2019 г.
^ Jump up to: Перейти обратно: ^а ^б «Идентичность – определение математического слова – Открытый справочник по математике» . www.mathopenref.com . Проверено 1 декабря 2019 г.
^ «Основные идентичности» . www.math.com . Проверено 1 декабря 2019 г.
^ «Алгебраические тождества» . www.sosmath.com . Проверено 1 декабря 2019 г.
^ Стапель, Элизабет. «Тригонометрические тождества» . Фиолетовая математика . Проверено 1 декабря 2019 г.
^ Бернштейн, Стивен; Бернштейн, Рут (1999), Очерк теории и проблем элементов статистики Шаума. I, Описательная статистика и вероятность , серия очерков Шаума, Нью-Йорк: McGraw-Hill , ISBN 978-0-07-005023-5 , с. 21
^ Осборн, Г. (1 января 1902 г.). «109. Мнемотехника для гиперболических формул» . Математический вестник . 2 (34): 189. дои : 10.2307/3602492 . JSTOR 3602492 .
^ Петерсон, Джон Чарльз (2003). Техническая математика с исчислением (3-е изд.). Cengage Обучение. п. 1155. ИСБН 0-7668-6189-9 . , глава 26, стр. 1155
^ Нахум Дершовиц ; Жан-Пьер Жуанно (1990). «Переписать системы». Ян ван Леувен (ред.). Формальные модели и семантика . Справочник по теоретической информатике. Том. Б. Эльзевир. стр. 243–320.
^ Вольфганг Векслер (1992). Вильфрид Брауэр ; Гжегож Розенберг ; Арто Саломаа (ред.). Универсальная алгебра для компьютерщиков . Монографии EATCS по теоретической информатике. Том. 25. Берлин: Шпрингер. ISBN 3-540-54280-9 . Здесь: Опр.1 п.3.2.1, стр.160.

Источники [ править ]

Даунинг, Дуглас (2003). Алгебра простой путь . Образовательная серия Бэрронса. ISBN 978-0-7641-1972-9 .
Кейт, СК; Бхапкар, HR (2009). Основы математики . Технические публикации. ISBN 978-81-8431-755-8 .
Ширали, С. (2002). Приключения в решении проблем . Университетская пресса. ISBN 978-81-7371-413-9 .

Внешние ссылки [ править ]

Энциклопедия уравнений Онлайн-энциклопедия математических тождеств (в архиве)
Коллекция алгебраических тождеств

[6] Все утверждения в этом разделе можно найти в Shirali 2002 , Раздел 4, Downing 2003 , p. 275, или Кейт и Бхапкар 2009 , с. Например, 1-1.

[:1-1] Jump up to: Перейти обратно: ^а ^б «Математические слова: идентичность» . www.mathwords.com . Проверено 1 декабря 2019 г.

[:2-2] Jump up to: Перейти обратно: ^а ^б «Идентичность – определение математического слова – Открытый справочник по математике» . www.mathopenref.com . Проверено 1 декабря 2019 г.

[3] «Основные идентичности» . www.math.com . Проверено 1 декабря 2019 г.

[4] «Алгебраические тождества» . www.sosmath.com . Проверено 1 декабря 2019 г.

[5] Стапель, Элизабет. «Тригонометрические тождества» . Фиолетовая математика . Проверено 1 декабря 2019 г.

[7] Бернштейн, Стивен; Бернштейн, Рут (1999), Очерк теории и проблем элементов статистики Шаума. I, Описательная статистика и вероятность , серия очерков Шаума, Нью-Йорк: McGraw-Hill , ISBN 978-0-07-005023-5 , с. 21

[8] Осборн, Г. (1 января 1902 г.). «109. Мнемотехника для гиперболических формул» . Математический вестник . 2 (34): 189. дои : 10.2307/3602492 . JSTOR 3602492 .

[9] Петерсон, Джон Чарльз (2003). Техническая математика с исчислением (3-е изд.). Cengage Обучение. п. 1155. ИСБН 0-7668-6189-9 . , глава 26, стр. 1155

[10] Нахум Дершовиц ; Жан-Пьер Жуанно (1990). «Переписать системы». Ян ван Леувен (ред.). Формальные модели и семантика . Справочник по теоретической информатике. Том. Б. Эльзевир. стр. 243–320.

[11] Вольфганг Векслер (1992). Вильфрид Брауэр ; Гжегож Розенберг ; Арто Саломаа (ред.). Универсальная алгебра для компьютерщиков . Монографии EATCS по теоретической информатике. Том. 25. Берлин: Шпрингер. ISBN 3-540-54280-9 . Здесь: Опр.1 п.3.2.1, стр.160.

[1]

[2]

[3]

[4]

[5]

[а]

[6]

[7]

[8]

[9]

[10]