Теорема Больцано – Вейерштрасса
В математике , особенно в реальном анализе , теорема Больцано-Вейерштрасса , названная в честь Бернара Больцано и Карла Вейерштрасса , является фундаментальным результатом о сходимости в конечномерном евклидовом пространстве. . Теорема утверждает, что каждая бесконечная ограниченная последовательность в имеет сходящуюся подпоследовательность . [1] Эквивалентная формулировка заключается в том, подмножество что тогда секвенциально компактна и только тогда, когда она замкнута и ограничена . [2] Эту теорему иногда называют теоремой секвенциальной компактности . [3]
История и значение
[ редактировать ]Теорема Больцано-Вейерштрасса названа в честь математиков Бернара Больцано и Карла Вейерштрасса . Фактически это было впервые доказано Больцано в 1817 году как лемма при доказательстве теоремы о промежуточном значении . Примерно пятьдесят лет спустя этот результат был признан значимым сам по себе и снова доказан Вейерштрассом. С тех пор это стало важной теоремой анализа .
Доказательство
[ редактировать ]Сначала докажем теорему для (набор всех действительных чисел ), и в этом случае порядок по можно использовать с пользой. Действительно, мы имеем следующий результат:
Лемма : Каждая бесконечная последовательность в имеет бесконечную монотонную подпоследовательность (подпоследовательность, которая является либо неубывающей , либо невозрастающей ).
Доказательство [4] : Назовем положительный целочисленный индекс последовательности — это «пик» последовательности, когда для каждого . Предположим сначала, что последовательность имеет бесконечно много вершин, а это значит, что существует подпоследовательность со следующими индексами и следующие условия . Итак, бесконечная последовательность в имеет монотонную (невозрастающую) подпоследовательность, то есть . Но предположим теперь, что существует лишь конечное число пиков, пусть быть конечным пиком, если он существует (пусть в противном случае) и пусть первый индекс новой подпоследовательности быть настроен на . Затем не является вершиной, так как наступает после финального пика, что предполагает существование с и . Снова, наступает после финального пика, следовательно, существует где с . Повторение этого процесса приводит к бесконечной неубывающей подпоследовательности , тем самым доказав, что каждая бесконечная последовательность в имеет монотонную подпоследовательность.
Теперь предположим, что у нас есть ограниченная последовательность в ; по доказанной выше лемме существует монотонная подпоследовательность, также ограниченная. следует Из теоремы о монотонной сходимости , что эта подпоследовательность сходится.
Наконец, общий случай ( ), можно свести к случаю следующим образом: дана ограниченная последовательность в , последовательность первых координат является ограниченной вещественной последовательностью, следовательно, она имеет сходящуюся подпоследовательность. Затем можно выделить подподпоследовательность, на которой сходятся вторые координаты, и так далее, пока в конце концов мы не перейдем от исходной последовательности к подпоследовательности. раз — что по-прежнему является подпоследовательностью исходной последовательности — в которой сходится каждая координатная последовательность, следовательно, сама подпоследовательность сходится.
Альтернативное доказательство
[ редактировать ]Существует также альтернативное доказательство теоремы Больцано-Вейерштрасса с использованием вложенных интервалов . Начнем с ограниченной последовательности :
- Потому что ограничена, эта последовательность имеет нижнюю границу и верхняя граница .
- Мы берем в качестве первого интервала последовательности вложенных интервалов.
- Затем мы разделились в середине на два подинтервала одинакового размера.
- Поскольку каждая последовательность имеет бесконечно много членов, должен быть (по крайней мере) один из этих подинтервалов, который содержит бесконечно много членов. . Примем этот подинтервал за второй интервал последовательности вложенных интервалов.
- Затем мы разделились снова в середине на два подинтервала одинакового размера.
- Опять же, один из этих подинтервалов содержит бесконечно много членов . Примем этот подинтервал за третий подинтервал последовательности вложенных интервалов.
- Мы продолжаем этот процесс бесконечно много раз. Таким образом мы получаем последовательность вложенных интервалов.
Поскольку мы уменьшаем длину интервала вдвое на каждом шаге, предел длины интервала равен нулю. Кроме того, по вложенных интервалах теореме о , которая гласит, что если каждый представляет собой замкнутый и ограниченный интервал, скажем
с
тогда, в предположении вложенности, пересечение не пуст. Таким образом, существует число это в каждом интервале . Теперь мы покажем, что является накопления местом .
Возьмите район из . Поскольку длина интервалов стремится к нулю, существует интервал это подмножество . Потому что содержит по построению бесконечно много членов и , также содержит бесконечно много членов . Это доказывает, что является местом накопления . Таким образом, существует подпоследовательность который сходится к .
Секвенциальная компактность в евклидовых пространствах
[ редактировать ]Определение: набор если секвенциально компактна, каждая последовательность в имеет сходящуюся подпоследовательность, сходящуюся к элементу .
Теорема: тогда секвенциально компактен и только тогда, когда замкнуто и ограничено .
Доказательство: ( секвенциальная компактность подразумевает замкнутость и ограниченность)
Предполагать является подмножеством со свойством, что каждая последовательность в имеет подпоследовательность, сходящую к элементу . Затем должна быть ограничена, так как в противном случае следующая неограниченная последовательность можно построить. Для каждого , определять быть любой произвольной точкой такой, что . Тогда каждая подпоследовательность неограниченно и, следовательно, не сходится. Более того, должна быть закрыта, так как любая предельная точка , который имеет последовательность точек в сходящаяся сама к себе, также должна лежать в .
Доказательство: (замкнутость и ограниченность подразумевают секвенциальную компактность )
С ограничена, любая последовательность также ограничен. Из теоремы Больцано-Вейерштрасса : содержит подпоследовательность, сходящую к некоторой точке . С является предельной точкой и представляет собой закрытое множество , должен быть элементом .
Таким образом, подмножества из для которого каждая последовательность из A имеет подпоследовательность, сходящуюся к элементу из – т. е. подмножества, секвенциально компактные в топологии подпространства – это в точности замкнутые и ограниченные подмножества.
В такой форме теоремы особенно ясна аналогия с теоремой Гейне–Бореля , которая утверждает, что подмножество компактно тогда и только тогда , когда оно замкнуто и ограничено. Фактически, общая топология говорит нам, что метризуемое пространство компактно тогда и только тогда, когда оно секвенциально компактно, так что теоремы Больцано-Вейерштрасса и Гейне-Бореля по сути одинаковы.
Приложение к экономике
[ редактировать ]В экономике существуют различные важные концепции равновесия , доказательства существования которых часто требуют вариаций теоремы Больцано – Вейерштрасса. Одним из примеров является существование эффективного по Парето распределения. Распределение представляет собой матрицу наборов потребления для агентов в экономике, и распределение является эффективным по Парето, если в него нельзя внести никаких изменений, которые не ухудшат положение ни одного агента и не сделают благосостояние хотя бы одного агента (здесь строки матрицы распределения должны быть ранжируемый по отношению предпочтения ). Теорема Больцано-Вейерштрасса позволяет доказать, что если множество распределений компактно и непусто , то система имеет распределение, эффективное по Парето.
См. также
[ редактировать ]- Последовательно компактное пространство
- Теорема Гейне – Бореля
- Полнота действительных чисел
- Вариационный принцип Экланда
Примечания
[ редактировать ]Ссылки
[ редактировать ]- Бартл, Роберт Г .; Шерберт, Дональд Р. (2000). Введение в реальный анализ (3-е изд.). Нью-Йорк: Дж. Уайли. ISBN 9780471321484 .
- Фитцпатрик, Патрик М. (2006). Расширенное исчисление (2-е изд.). Бельмонт, Калифорния: Томсон Брукс/Коул. ISBN 0-534-37603-7 .
























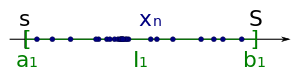
![{\displaystyle I_{1}=[s,S]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/58be63fbf6d3dff28ca6747569a558d5af61740e)


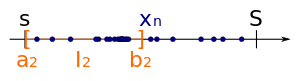


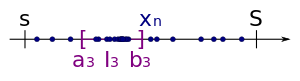

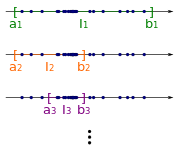

![{\displaystyle I_{n}=[a_{n},\,b_{n}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7d87f6f5ae37e6fb5ecb4ab2d9c16e5275221650)












