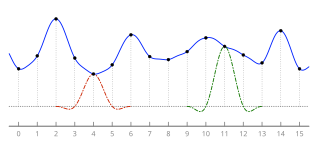
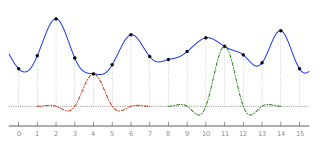
Передискретизация Ланцоша

Частичный график дискретного сигнала (черные точки) и его интерполяции Ланцоша (сплошная синяя кривая) с параметром размера a, равным 1 (вверху), 2 (в центре) и 3 (внизу). Также показаны две копии ядра Ланцоша, сдвинутые и масштабированные, соответствующие образцам 4 и 11 (пунктирные кривые).

Фильтрация Ланцоша и повторная выборка Ланцоша — это два применения математической формулы. Его можно использовать в качестве фильтра нижних частот или для плавной интерполяции значения цифрового сигнала между его выборками . В последнем случае он сопоставляет каждую выборку данного сигнала с преобразованной и масштабированной копией ядра Ланцоша , которое представляет собой функцию sinc, окруженную центральным лепестком второй, более длинной функции sinc. Сумма этих переведенных и масштабированных ядер затем оценивается в нужных точках.

Повторная дискретизация Ланцоша обычно используется для увеличения частоты дискретизации цифрового сигнала или для его смещения на часть интервала дискретизации. Он также часто используется для многомерной интерполяции , например, для изменения размера или поворота цифрового изображения . Для этой цели он считается «лучшим компромиссом» среди нескольких простых фильтров. ^[1]

Фильтр был изобретен Клодом Дюшоном , который назвал его в честь Корнелиуса Ланцоша из-за использования Дюшоном сигма-аппроксимации при построении фильтра, метода, созданного Ланцошем. ^[2]

Определение

Ядро Ланцоша

Ядра Ланцоша для случаев a = 2 и a = 3. Обратите внимание, что функция принимает отрицательные значения.

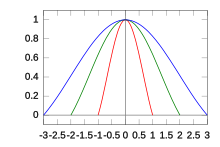
фильтра Влияние каждой входной выборки на интерполированные значения определяется ядром реконструкции $L (x)$ , называемым ядром Ланцоша. Это нормализованная sinc функция $sinc(x)$ , оконная (умноженная) на окно Ланцоша , или окно sinc , которое является центральным лепестком горизонтально растянутой функции sinc $sinc(x / a)$ для $- a \leq x \leq a$ .

L(x)={\begin{cases}\operatorname {sinc} (x)\operatorname {sinc} (x/a)&{\text{if}}\ -a<x<a,\\0&{\text{otherwise}}.\end{cases}}

Эквивалентно,

L(x)={\begin{cases}1&{\text{if}}\ x=0,\\{\dfrac {a\sin(\pi x)\sin(\pi x/a)}{\pi ^{2}x^{2}}}&{\text{if}}\ -a\leq x<a\ {\text{and}}\ x\neq 0,\\0&{\text{otherwise}}.\end{cases}}

Параметр $a$ представляет собой целое положительное число, обычно 2 или 3, которое определяет размер ядра. Ядро Ланцоша имеет $2 a - 1$ доли: положительную в центре и $a - 1$ чередующиеся отрицательные и положительные доли с каждой стороны.

Формула интерполяции

Учитывая одномерный сигнал с выборками $s i$ , для целых значений $i$ значение $S (x),$ интерполированное при произвольном вещественном аргументе $x,$ получается путем дискретной свертки этих выборок с ядром Ланцоша: ^[3]

S(x)=\sum _{i=\lfloor x\rfloor -a+1}^{\lfloor x\rfloor +a}s_{i}L(x-i),

где $a$ — параметр размера фильтра, а $\lfloor x\rfloor$ это функция пола . Границы этой суммы таковы, что вне их ядро равно нулю.

Характеристики

Пока параметр $a$ является положительным целым числом, ядро Ланцоша непрерывно всюду, а его производная определена и непрерывна всюду (даже при $x = \pm a$ , где обе функции sinc обращаются к нулю). Следовательно, восстановленный сигнал $S (x)$ тоже будет непрерывным, с непрерывной производной.

Ядро Ланцоша равно нулю для каждого целочисленного аргумента $x$ , за исключением $x = 0$ , где оно имеет значение 1. Следовательно, восстановленный сигнал точно интерполирует заданные выборки: мы будем иметь $S (x) = s i$ для каждого целочисленного аргумента $x = я$ .

Повторная выборка Ланцоша - это одна из форм общего метода, разработанного Ланцошем для противодействия феномену Гиббса путем умножения коэффициентов усеченного ряда Фурье на $\mathrm {sinc} (\pi k/m)$ , где $k$ – индекс коэффициента и $m$ это то, сколько коэффициентов мы сохраняем. ^[4] Те же рассуждения применимы и в случае усеченных функций, если мы хотим удалить из их спектра колебания Гиббса.

Многомерная интерполяция

Ядро фильтра Ланцоша в двух измерениях:

L(x,y)=L(x)L(y).

Оценка

Преимущества

Теоретически оптимальным фильтром восстановления для сигналов с ограниченной полосой пропускания является sinc-фильтр , имеющий бесконечную поддержку . Фильтр Ланцоша — одна из многих практических (конечно поддерживаемых) аппроксимаций фильтра sinc. Каждое интерполированное значение представляет собой взвешенную сумму $двух последовательных$ входных выборок. Таким образом, изменяя $параметр 2 a$ , можно обменять скорость вычислений на улучшение частотной характеристики. Параметр также позволяет выбирать между более плавной интерполяцией или сохранением резких переходных процессов в данных. При обработке изображений приходится искать компромисс между уменьшением артефактов сглаживания и сохранением резких краев. Также, как и при любой подобной обработке, границы изображения не получают результатов. Увеличение длины ядра увеличивает обрезку краев изображения.

Фильтр Ланцоша сравнивался с другими методами интерполяции дискретных сигналов, особенно с другими оконными версиями sinc-фильтра. Турковски и Габриэль утверждали, что фильтр Ланцоша (с $a = 2$ ) является «лучшим компромиссом с точки зрения уменьшения наложения спектров, резкости и минимального звона» по сравнению с усеченным sinc и sinc с окнами Бартлетта , косинуса и Ханна . для прореживания и интерполяции данных двумерного изображения. ^[1] По словам Джима Блинна , ядро Ланцоша (с $= 3$ ) «сохраняет низкие частоты и подавляет высокие частоты лучше, чем любой (достижимый) фильтр, который мы видели до сих пор». ^[5]

Интерполяция Ланцоша — популярный фильтр для «масштабирования» видео в различных медиа-утилитах, таких как AviSynth. ^[6] и FFmpeg . ^[7]

Ограничения

Поскольку ядро принимает отрицательные значения для $a > 1$ , интерполированный сигнал может быть отрицательным, даже если все выборки положительны. В более общем смысле, диапазон значений интерполированного сигнала может быть шире, чем диапазон, охватываемый значениями дискретных выборок. В частности, могут возникать артефакты звона непосредственно перед и после резких изменений значений выборки, что может привести к артефактам отсечения . Однако эти эффекты уменьшаются по сравнению с (неоконным) sinc-фильтром. При а = 2 (трехлопастное ядро) звон < 1%.

При использовании фильтра Ланцоша для повторной выборки изображения эффект звона создаст светлые и темные ореолы вдоль любых резких краев. Хотя эти полосы могут раздражать визуально, они помогают повысить воспринимаемую резкость и, следовательно, обеспечивают своего рода усиление краев . Это может улучшить субъективное качество изображения, учитывая особую роль резкости краев в зрении . ^[8]

В некоторых приложениях артефакты отсечения нижних частот можно устранить путем преобразования данных в логарифмическую область перед фильтрацией. В этом случае интерполированные значения будут представлять собой среднее геометрическое, а не среднее арифметическое входных выборок.

Ядро Lanczos не имеет раздела со свойством единства . То есть сумма ${\textstyle U(x)=\sum _{i\in \mathbb {Z} }L(x-i)}$ всех копий ядра, преобразованных целыми числами, не всегда равно 1. Следовательно, интерполяция Ланцоша дискретного сигнала с постоянными выборками не дает постоянной функции. Этот дефект наиболее очевиден при $a = 1$ . Кроме того, для $a = 1$ интерполированный сигнал имеет нулевую производную для каждого целочисленного аргумента. Это довольно академично, поскольку использование однолепесткового ядра ( a = 1) теряет все преимущества подхода Ланцоша и обеспечивает плохой фильтр. Есть много лучших однолепестковых колоколообразных оконных функций.

См. также

Ссылки

^ Jump up to: ^а ^б Турковски, Кен; Габриэль, Стив (1990). «Фильтры для распространенных задач повторной выборки». В Гласснере, Эндрю С. (ред.). Графические драгоценности I. Академическая пресса. стр. 147–165. CiteSeerX 10.1.1.116.7898 . ISBN 978-0-12-286165-9 .
^ Клод, Дюшон (1 августа 1979 г.). «Фильтрация Ланцоша в одном и двух измерениях» . Журнал прикладной метеорологии . 18 (8): 1016–1022. Бибкод : 1979JApMe..18.1016D . doi : 10.1175/1520-0450(1979)018<1016:LFIOAT>2.0.CO;2 .
^ Бургер, Вильгельм; Бердж, Марк Дж. (2009). Принципы цифровой обработки изображений: основные алгоритмы . Спрингер. стр. 231–232. ISBN 978-1-84800-194-7 .
^ Ланцос, Корнелиус (1988). Прикладной анализ . Нью-Йорк: Dover Publications. стр. 219–221. ISBN 0-486-65656-Х . OCLC 17650089 .
^ Блинн, Джим (1998). Уголок Джима Блинна: грязные пиксели . Морган Кауфманн. стр. 26–27. ISBN 978-1-55860-455-1 .
^ «Изменить размер» . Ависинт. 01.01.2015 . Проверено 27 июля 2015 г.
^ «Практическое руководство: преобразование видео с повышением частоты с помощью FFDShow — форумы Neowin» . Neowin.net. 18 апреля 2006 г. Проверено 31 июля 2012 г.
^ «IPOL: Линейные методы интерполяции изображений» . Ипол.им. 27 сентября 2011 г. Проверено 31 июля 2012 г.

Внешние ссылки

Примеры антизерновой геометрии : image_filters.cpp показывает сравнение многократной повторной выборки изображения с различными ядрами.
imageresampler : общедоступный класс передискретизации изображений на C++ с поддержкой нескольких оконных ядер фильтров Lanczos.

[turkgab-1] Jump up to: ^а ^б Турковски, Кен; Габриэль, Стив (1990). «Фильтры для распространенных задач повторной выборки». В Гласснере, Эндрю С. (ред.). Графические драгоценности I. Академическая пресса. стр. 147–165. CiteSeerX 10.1.1.116.7898 . ISBN 978-0-12-286165-9 .

[duchon-2] Клод, Дюшон (1 августа 1979 г.). «Фильтрация Ланцоша в одном и двух измерениях» . Журнал прикладной метеорологии . 18 (8): 1016–1022. Бибкод : 1979JApMe..18.1016D . doi : 10.1175/1520-0450(1979)018<1016:LFIOAT>2.0.CO;2 .

[burger-3] Бургер, Вильгельм; Бердж, Марк Дж. (2009). Принципы цифровой обработки изображений: основные алгоритмы . Спрингер. стр. 231–232. ISBN 978-1-84800-194-7 .

[4] Ланцос, Корнелиус (1988). Прикладной анализ . Нью-Йорк: Dover Publications. стр. 219–221. ISBN 0-486-65656-Х . OCLC 17650089 .

[5] Блинн, Джим (1998). Уголок Джима Блинна: грязные пиксели . Морган Кауфманн. стр. 26–27. ISBN 978-1-55860-455-1 .

[6] «Изменить размер» . Ависинт. 01.01.2015 . Проверено 27 июля 2015 г.

[7] «Практическое руководство: преобразование видео с повышением частоты с помощью FFDShow — форумы Neowin» . Neowin.net. 18 апреля 2006 г. Проверено 31 июля 2012 г.

[8] «IPOL: Линейные методы интерполяции изображений» . Ипол.им. 27 сентября 2011 г. Проверено 31 июля 2012 г.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]