Метод прогулки по сферам

В математике метод ходьбы по сферам (WoS) — это численный вероятностный алгоритм или метод Монте-Карло , используемый в основном для аппроксимации решений некоторой конкретной краевой задачи для уравнений в частных производных (УЧП). ^[1]^[2] Метод WoS был впервые представлен Мервином Э. Мюллером в 1956 году для решения уравнения Лапласа : ^[1] и с тех пор был распространен на другие проблемы.

Он опирается на вероятностные интерпретации PDE и моделирует траектории броуновского движения (или, в некоторых более общих вариантах, диффузионных процессов ). путем выборки только точек выхода из последовательных сфер, вместо того, чтобы детально моделировать путь процесса. Это часто делает его менее затратным, чем «сеточные» алгоритмы, и сегодня это один из наиболее широко используемых «бессеточных» алгоритмов для генерации броуновских путей.

Неофициальное описание

Позволять $\Omega$ быть ограниченной областью в $\mathbb {R} ^{d}$ с достаточно регулярной границей $\Gamma$ , пусть h — функция на $\Gamma$ , и пусть $x$ быть точкой внутри $\Omega$ .

Рассмотрим задачу Дирихле :

{\begin{cases}\Delta u(x)=0&{\mbox{if }}x\in \Omega \\u(x)=h(x)&{\mbox{if }}x\in \Gamma .\end{cases}}

Это можно легко показать ^[а] что когда решение $u$ существует, для $x\in \Omega$ :

u(x)=\mathbb {E} _{x}[h(W_{\tau })]

где $W$ — $d$ -мерный винеровский процесс , математическое ожидание берется условно на ${W0 τ = x}$ , а $—$ время первого выхода из $Ω$ .

Чтобы вычислить решение с использованием этой формулы, нам нужно всего лишь смоделировать первую точку выхода независимых броуновских путей, поскольку согласно закону больших чисел :

\mathbb {E} _{x}[h(W_{\tau })]\sim {\frac {1}{n}}\sum _{i=1}^{n}h(W_{\tau }^{i})

Метод WoS обеспечивает эффективный способ выборки первой точки выхода броуновского движения из области, отмечая, что для любой $(d - 1)$ -сферы с центром в $x$ первая точка выхода $W$ из сферы имеет равномерное распределение по его поверхности. Таким образом, оно начинается с $x (0)$ равен $x$ и рисует самую большую сферу ${\mathcal {S}}_{0}$ с центром по $х (0)$ и содержится внутри домена. Первая точка выхода $x (1)$ от ${\mathcal {S}}_{0}$ равномерно распределяется по его поверхности. Индуктивно повторяя этот шаг, WoS предоставляет последовательность $(x (н))$ положений броуновского движения.

По интуиции процесс будет сходиться к первой точке выхода из области. Однако для завершения этого алгоритма почти наверняка потребуется бесконечное количество шагов. Для вычислительной реализации процесс обычно останавливается, когда он приближается достаточно близко к границе, и возвращает проекцию процесса на границе. Эту процедуру иногда называют введением $\varepsilon$ -раковина, или $\varepsilon$ -слой. ^[4]

Формулировка метода

Выбирать $\varepsilon >0$ . Используя те же обозначения, что и выше, алгоритм «Прогулки по сферам» описывается следующим образом:

Инициализировать: $x^{(0)}=x$
Пока $d(x^{(n)},\Gamma )>\varepsilon$ $d(x^{(n)},\Gamma)>\varepsilon$ :
1. Набор $r_{n}=d(x^{(n)},\Gamma )$ .
2. Образец $\gamma _{n}$ вектор, равномерно распределенный по единичной сфере, независимо от предыдущих.
3. Набор $x^{(n+1)}:=x^{(n)}+r_{n}\gamma _{n}$
Когда $d(x^{(n)},\Gamma )\leq \varepsilon$ :
$x_{f}:=p_{\Gamma }(x^{(n)})$ , ортогональная проекция $x^{(n)}$ на $\Gamma$
Возвращаться $x_{f}$

Результат $x_{f}$ является оценкой первой точки выхода из $\Omega$ винеровского процесса, начиная с $x$ , в том смысле, что они имеют близкие распределения вероятностей (комментарии к ошибке см. ниже).

Комментарии и практические соображения

Радиус сфер

В некоторых случаях расстояние до границы может быть трудно вычислить, и тогда предпочтительнее заменить радиус сферы нижней границей этого расстояния. Затем необходимо обеспечить, чтобы радиус сфер оставался достаточно большим, чтобы процесс достиг границы. ^[1]

Смещение в методе и GFFP

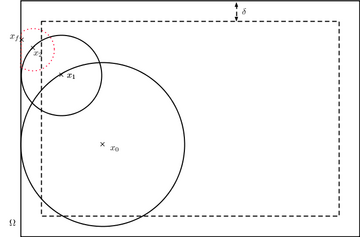
Поскольку это метод Монте-Карло, ошибку оценщика можно разложить на сумму систематической ошибки и статистической ошибки . Статистическая ошибка уменьшается за счет увеличения количества выбранных путей или использования методов уменьшения дисперсии .

WoS теоретически обеспечивает точное (или объективное) моделирование траекторий броуновского движения. Однако, как сформулировано здесь, $\varepsilon$ -shell, введенный для обеспечения завершения алгоритма, также добавляет ошибку, обычно порядка ${\mathcal {O}}(\varepsilon )$ . ^[4] Эта ошибка была изучена, и ее можно избежать в некоторых геометриях, используя метод первого прохода функций Грина : ^[5] можно изменить геометрию «сфер», находясь достаточно близко к границе, так что вероятность достижения границы за один шаг станет положительной. Это требует знания функций Грина для конкретных областей. (см. также Гармоническую меру )

Когда есть возможность его использовать, обычно предпочтительнее метод первого прохода функции Грина (GFFP), поскольку он быстрее и точнее, чем классический WoS. ^[4]

Сложность

Можно показать, что количество шагов, предпринятых процессом WoS для достижения $\varepsilon$ -раковина в порядке ${\mathcal {O}}(|\log(\varepsilon )|)$ . ^[2] Таким образом, можно в определенной степени повысить точность, не увеличивая при этом заметно число шагов.

Как это обычно бывает с методами Монте-Карло, этот алгоритм работает особенно хорошо, когда размерность превышает $3$ , и нужен только небольшой набор значений. Действительно, вычислительные затраты растут линейно с увеличением размерности, тогда как стоимость сеточно-зависимых методов увеличивается экспоненциально с увеличением размерности. ^[2]

Варианты, расширения

Этот метод широко изучен, обобщен и усовершенствован. Например, сейчас он широко используется для расчета физических свойств материалов (таких как емкость , электростатическая внутренняя энергия молекул и т. д.). Некоторые известные расширения включают в себя:

Эллиптические уравнения

Метод WoS можно модифицировать для решения более общих задач. В частности, метод обобщен на решение задач Дирихле для уравнений вида $\Delta u=cu+f$ ^[6] (которые включают уравнения Пуассона и линеаризованные уравнения Пуассона-Больцмана ) или для любого эллиптического уравнения в частных производных с постоянными коэффициентами. ^[7]

Также были разработаны более эффективные способы решения линеаризованного уравнения Пуассона-Больцмана, основанные на Фейнмана-Каца . представлениях решений ^[8]

Зависимость от времени

Опять же, в достаточно регулярных границах можно использовать метод WoS для решения следующей задачи:

{\begin{cases}\partial _{t}u(x,t)+{\frac {1}{2}}\Delta _{x}u(x,t)=0&{\mbox{if }}x\in \Omega {\mbox{ and }}t<T\\u(x,T)=h(x,T)&{\mbox{if }}x\in {\bar {\Omega }}\\u(x,t)=h(x,t)&{\mbox{if }}x\in \Gamma .\end{cases}}

из которых решение можно представить в виде: ^[9]

u(x,t)=\mathbb {E} _{t,x}(h(X_{T\wedge \tau },T\wedge \tau ))

,

где математическое ожидание берется условно $X_{t}=x$

Чтобы использовать WoS с помощью этой формулы, необходимо выбрать время выхода из каждой нарисованной сферы, которое является независимой переменной. $\tau _{0}$ с преобразованием Лапласа (для сферы радиуса $R$ ): ^[10]

\mathbb {E} (\exp(-s\tau _{0}))={\frac {R{\sqrt {2s}}}{\sinh(R{\sqrt {2s}})}}

Общее время выхода из домена $\tau$ может быть вычислено как сумма времен выхода из сфер. Процесс также необходимо остановить, если он вовремя не вышел из домена. $T$ .

Другие расширения

Метод WoS был обобщен для оценки решения эллиптических уравнений в частных производных повсюду в области, а не в одной точке. ^[11]

Метод WoS также был обобщен для расчета времени попадания для процессов, отличных от броуновских движений. Например, время прохождения процессов Бесселя можно вычислить с помощью алгоритма под названием «Прогулка по движущимся сферам». ^[12] Эта проблема имеет приложения в математических финансах.

WoS можно адаптировать для решения уравнений Пуассона и Пуассона – Больцмана с условиями потока на границе. ^[13]

Наконец, WoS можно использовать для решения задач, в которых коэффициенты непрерывно изменяются в пространстве, посредством связи с уравнением объемной рендеринга. ^[14]

См. также

Формула Фейнмана – Каца
Случайные процессы и краевые задачи
Метод Эйлера-Маруямы для определения путей общих диффузионных процессов.

Примечания

^ Связь была впервые установлена Какутани для двумерного броуновского движения. ^[3] теперь его можно рассматривать как тривиальный случай формулы Фейнмана-Каца.

Ссылки

^ Jump up to: ^а ^б ^с Мюллер, Мервин Э. (сентябрь 1956 г.). «Некоторые непрерывные методы Монте-Карло для задачи Дирихле» . Анналы математической статистики . 27 (3): 569–589. дои : 10.1214/aoms/1177728169 . JSTOR 2237369 .
^ Jump up to: ^а ^б ^с Сабельфельд, Карл К. (1991). Методы Монте-Карло в краевых задачах . Берлин [и др.]: Springer-Verlag. ISBN 978-3540530015 .
^ Какутани, Шизуо (1944). «Двумерное броуновское движение и гармонические функции» . Известия Императорской Академии . 20 (10): 706–714. дои : 10.3792/пиа/1195572706 .
^ Jump up to: ^а ^б ^с Масканьи, Майкл; Хван, Чи-Ок (июнь 2003 г.). «Анализ ошибок ϵ-Shell для алгоритмов «Хождение по сферам»». Математика и компьютеры в моделировании . 63 (2): 93–104. дои : 10.1016/S0378-4754(03)00038-7 .
^ Учитывая, Джеймс А.; Хаббард, Джозеф Б.; Дуглас, Джек Ф. (1997). «Алгоритм первого прохода для гидродинамического трения и скорости реакции макромолекул, ограниченной диффузией» . Журнал химической физики . 106 (9): 3761. Бибкод : 1997ЖЧФ.106.3761Г . дои : 10.1063/1.473428 .
^ Елепов, Б.С.; Михайлов Г.А. (январь 1969 г.). «Решение задачи Дирихле для уравнения Δ u − cu = − q по модели «блуждания по сферам» ». Вычислительная математика и математическая физика СССР . 9 (3): 194–204. дои : 10.1016/0041-5553(69)90070-6 .
^ Бут, Томас Э. (февраль 1981 г.). «Точное решение Монте-Карло эллиптических уравнений в частных производных». Журнал вычислительной физики . 39 (2): 396–404. Бибкод : 1981JCoPh..39..396B . дои : 10.1016/0021-9991(81)90159-5 .
^ Хван, Чи-Ок; Масканьи, Майкл; Учитывая, Джеймс А. (март 2003 г.). «Реализация интеграла по путям Фейнмана – Каца для уравнения Пуассона с использованием h -обусловленной функции Грина». Математика и компьютеры в моделировании . 62 (3–6): 347–355. CiteSeerX 10.1.1.123.3156 . дои : 10.1016/S0378-4754(02)00224-0 .
^ Гобе, Эммануэль (2013). Методы Монте-Карло и случайные процессы от линейных к нелинейным . Палезо: Editions de l’Ecole Polytechnique. ISBN 978-2-7302-1616-6 .
^ Салминен, Андрей Н. Бородин; Пааво (2002). Справочник по броуновскому движению: факты и формулы (2-е изд.). Базель [ua]: Биркхойзер. ISBN 978-3-7643-6705-3 . {{cite book}}: CS1 maint: несколько имен: список авторов ( ссылка )
^ Бут, Томас (август 1982 г.). «Региональное решение Монте-Карло эллиптических уравнений в частных производных» (PDF) . Журнал вычислительной физики . 47 (2): 281–290. Бибкод : 1982JCoPh..47..281B . дои : 10.1016/0021-9991(82)90079-1 .
^ Дьякону, Мадалина; Херрманн, Самуэль (декабрь 2013 г.). «Время достижения процессов Бесселя - алгоритм прогулки по движущимся сферам (WoMS)». Анналы прикладной теории вероятности . 23 (6): 2259–2289. arXiv : 1111.3736 . дои : 10.1214/12-AAP900 . S2CID 25036031 .
^ Симонов, Николай А. (2007). «Случайные блуждания для решения краевых задач с потоковыми условиями». Численные методы и приложения . Конспекты лекций по информатике. Том. 4310. стр. 181–188. CiteSeerX 10.1.1.63.3780 . дои : 10.1007/978-3-540-70942-8_21 . ISBN 978-3-540-70940-4 .
^ Сони, Рохан; Сейб, Дарио; Ярош, Войцех; Крейн, Кинан (июль 2022 г.). «Бессеточный Монте-Карло для УЧП с пространственно меняющимися коэффициентами». Транзакции ACM с графикой . 41 (4): 1–17. arXiv : 2201.13240 . дои : 10.1145/3528223.3530134 . S2CID 246430740 .

Дальнейшее чтение

Сабельфельд, Карл К. (1991). Методы Монте-Карло в краевых задачах . Берлин [и др.]: Springer-Verlag. ISBN 9783540530015 .

Внешние ссылки

Некоторые непрерывные методы Монте-Карло для задачи Дирихле. Статья, в которой Марвин Эдгар Мюллер представил этот метод.
Броуновское движение Питера Мёртерса и Юваля Переса. См. главу 3.3 о гармонической мере, функциях Грина и точках выхода.

[4] Связь была впервые установлена Какутани для двумерного броуновского движения. ^[3] теперь его можно рассматривать как тривиальный случай формулы Фейнмана-Каца.

[muller-1] Jump up to: ^а ^б ^с Мюллер, Мервин Э. (сентябрь 1956 г.). «Некоторые непрерывные методы Монте-Карло для задачи Дирихле» . Анналы математической статистики . 27 (3): 569–589. дои : 10.1214/aoms/1177728169 . JSTOR 2237369 .

[sabelfeld-2] Jump up to: ^а ^б ^с Сабельфельд, Карл К. (1991). Методы Монте-Карло в краевых задачах . Берлин [и др.]: Springer-Verlag. ISBN 978-3540530015 .

[3] Какутани, Шизуо (1944). «Двумерное броуновское движение и гармонические функции» . Известия Императорской Академии . 20 (10): 706–714. дои : 10.3792/пиа/1195572706 .

[mascagniEpsilonShell-5] Jump up to: ^а ^б ^с Масканьи, Майкл; Хван, Чи-Ок (июнь 2003 г.). «Анализ ошибок ϵ-Shell для алгоритмов «Хождение по сферам»». Математика и компьютеры в моделировании . 63 (2): 93–104. дои : 10.1016/S0378-4754(03)00038-7 .

[6] Учитывая, Джеймс А.; Хаббард, Джозеф Б.; Дуглас, Джек Ф. (1997). «Алгоритм первого прохода для гидродинамического трения и скорости реакции макромолекул, ограниченной диффузией» . Журнал химической физики . 106 (9): 3761. Бибкод : 1997ЖЧФ.106.3761Г . дои : 10.1063/1.473428 .

[7] Елепов, Б.С.; Михайлов Г.А. (январь 1969 г.). «Решение задачи Дирихле для уравнения Δ u − cu = − q по модели «блуждания по сферам» ». Вычислительная математика и математическая физика СССР . 9 (3): 194–204. дои : 10.1016/0041-5553(69)90070-6 .

[8] Бут, Томас Э. (февраль 1981 г.). «Точное решение Монте-Карло эллиптических уравнений в частных производных». Журнал вычислительной физики . 39 (2): 396–404. Бибкод : 1981JCoPh..39..396B . дои : 10.1016/0021-9991(81)90159-5 .

[9] Хван, Чи-Ок; Масканьи, Майкл; Учитывая, Джеймс А. (март 2003 г.). «Реализация интеграла по путям Фейнмана – Каца для уравнения Пуассона с использованием h -обусловленной функции Грина». Математика и компьютеры в моделировании . 62 (3–6): 347–355. CiteSeerX 10.1.1.123.3156 . дои : 10.1016/S0378-4754(02)00224-0 .

[10] Гобе, Эммануэль (2013). Методы Монте-Карло и случайные процессы от линейных к нелинейным . Палезо: Editions de l’Ecole Polytechnique. ISBN 978-2-7302-1616-6 .

[11] Салминен, Андрей Н. Бородин; Пааво (2002). Справочник по броуновскому движению: факты и формулы (2-е изд.). Базель [ua]: Биркхойзер. ISBN 978-3-7643-6705-3 . {{cite book}}: CS1 maint: несколько имен: список авторов ( ссылка )

[12] Бут, Томас (август 1982 г.). «Региональное решение Монте-Карло эллиптических уравнений в частных производных» (PDF) . Журнал вычислительной физики . 47 (2): 281–290. Бибкод : 1982JCoPh..47..281B . дои : 10.1016/0021-9991(82)90079-1 .

[13] Дьякону, Мадалина; Херрманн, Самуэль (декабрь 2013 г.). «Время достижения процессов Бесселя - алгоритм прогулки по движущимся сферам (WoMS)». Анналы прикладной теории вероятности . 23 (6): 2259–2289. arXiv : 1111.3736 . дои : 10.1214/12-AAP900 . S2CID 25036031 .

[14] Симонов, Николай А. (2007). «Случайные блуждания для решения краевых задач с потоковыми условиями». Численные методы и приложения . Конспекты лекций по информатике. Том. 4310. стр. 181–188. CiteSeerX 10.1.1.63.3780 . дои : 10.1007/978-3-540-70942-8_21 . ISBN 978-3-540-70940-4 .

[15] Сони, Рохан; Сейб, Дарио; Ярош, Войцех; Крейн, Кинан (июль 2022 г.). «Бессеточный Монте-Карло для УЧП с пространственно меняющимися коэффициентами». Транзакции ACM с графикой . 41 (4): 1–17. arXiv : 2201.13240 . дои : 10.1145/3528223.3530134 . S2CID 246430740 .

[1]

[2]

[а]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[3]