Алгоритмы масштабирования пиксель-арта

Размер спрайта телевизора (в центре) изменен с использованием простого масштабирования по ближайшему соседу (слева) и алгоритма интерполяции 2xSaI (справа)

Сравнение распространенных алгоритмов масштабирования пиксельной графики. Посмотрите в полном разрешении, чтобы увидеть различия.

Алгоритмы масштабирования пиксельной графики представляют собой графические фильтры, которые пытаются улучшить внешний вид нарисованной от руки 2D- пиксельной графики. Эти алгоритмы представляют собой форму автоматического улучшения изображения. Алгоритмы масштабирования пиксельной графики используют методы, существенно отличающиеся от обычных методов масштабирования изображений , целью которых является сохранение внешнего вида изображений.

Поскольку пиксельная графика обычно используется с очень низким разрешением , в ней используется тщательная окраска отдельных пикселей. В результате получается графика, основанная на большом количестве стилизованных визуальных подсказок для определения сложных форм. Несколько специализированных алгоритмов были разработаны для повторного масштабирования такой графики.

Эти специализированные алгоритмы могут улучшить внешний вид пиксельной графики, но при этом они вносят изменения. Такие изменения могут быть нежелательны, особенно если цель состоит в том, чтобы точно воспроизвести первоначальный внешний вид.

Поскольку типичным применением этой технологии является улучшение внешнего вида четвертого поколения и более ранних версий видеоигр на аркадных и консольных эмуляторах , многие алгоритмы масштабирования пиксельной графики предназначены для работы в реальном времени для достаточно небольших входных изображений со скоростью 60 кадров в секунду . Это накладывает ограничения на тип методов программирования , которые можно использовать для такого рода обработки в реальном времени. Многие работают только с конкретными масштабными коэффициентами. 2× является наиболее распространенным масштабным коэффициентом, а 3×, 4×, 5× и 6× существуют, но используются реже.

Алгоритмы

SAA5050 «Диагональное сглаживание»

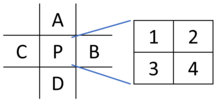
Чип генератора символов телетекста Mullard SAA5050 (1980 г.) использовал примитивный алгоритм масштабирования пикселей для генерации символов с более высоким разрешением на экране из представления с более низким разрешением из своего внутреннего ПЗУ. Внутри каждая форма символа определялась в сетке пикселей 5 × 9 , которая затем интерполировалась путем сглаживания диагоналей, чтобы получить символ размером 10 × 18 пикселей с характерной угловатой формой, окруженный сверху и слева двумя пикселями пустого пространства. . Алгоритм работает только с монохромными исходными данными и предполагает, что исходные пиксели будут логически истинными или ложными в зависимости от того, «включены» они или «выключены». Предполагается, что пиксели «вне сетки» отключены.

Алгоритм работает следующим образом:

A B C --\ 1 2
D E F --/ 3 4

1 = B | (A & E & !B & !D)
2 = B | (C & E & !B & !F)
3 = E | (!A & !E & B & D)
4 = E | (!C & !E & B & F) 

Обратите внимание, что этот алгоритм, как и приведенный ниже алгоритм Игла, имеет недостаток: Если появится узор из 4 пикселей в форме полого ромба, полость будет скрыта при расширении. Внутреннее ПЗУ символов SAA5050 тщательно избегает использования этого шаблона.

Вырожденный случай:

 *
* *
 *

становится:

  **  
 **** 

 ****
  **

EPX/Масштаб2×/AdvMAME2×

Расширение пикселей Эрика (EPX) — это алгоритм, разработанный Эриком Джонстоном из LucasArts примерно в 1992 году при переносе игр на движке SCUMM с IBM PC (который работал с разрешением 320 × 200 × 256 цветов) на ранние цветные компьютеры Macintosh, которые работали на более высокой скорости. или менее вдвое больше этого разрешения. Алгоритм работает следующим образом, расширяя P на 4 новых пикселя в зависимости от окружения P:

 1=P; 2=P; 3=P; 4=P;
 IF C==A => 1=A
 IF A==B => 2=B
 IF D==C => 3=C
 IF B==D => 4=D
 IF of A, B, C, D, three or more are identical: 1=2=3=4=P

Более поздние реализации того же алгоритма (например, AdvMAME2× и Scale2×, разработанные примерно в 2001 году) немного более эффективны, но функционально идентичны:

 1=P; 2=P; 3=P; 4=P;
 IF C==A AND C!=D AND A!=B => 1=A
 IF A==B AND A!=C AND B!=D => 2=B
 IF D==C AND D!=B AND C!=A => 3=C
 IF B==D AND B!=A AND D!=C => 4=D

AdvMAME2× доступен в DOSBox через scaler=advmame2x опция dosbox.conf .

Алгоритм AdvMAME4×/Scale4× представляет собой простое применение EPX дважды для получения разрешения 4×.

Scale3×/AdvMAME3× и ScaleFX

EPX можно использовать для масштабирования растровых шрифтов. Сверху вниз: а) исходный размер шрифта; б) 2× масштабирование ближайшего соседа; в) масштабирование EPX 2×; г) 3-кратное масштабирование ближайшего соседа; д) Масштабирование EPX 3×.

Алгоритм AdvMAME3×/Scale3× (доступен в DOSBox через scaler=advmame3x dosbox.conf ) можно рассматривать как обобщение EPX на случай 3×. Угловые пиксели рассчитываются идентично EPX.

 1=E; 2=E; 3=E; 4=E; 5=E; 6=E; 7=E; 8=E; 9=E;
 IF D==B AND D!=H AND B!=F => 1=D
 IF (D==B AND D!=H AND B!=F AND E!=C) OR (B==F AND B!=D AND F!=H AND E!=A) => 2=B
 IF B==F AND B!=D AND F!=H => 3=F
 IF (H==D AND H!=F AND D!=B AND E!=A) OR (D==B AND D!=H AND B!=F AND E!=G) => 4=D
 5=E
 IF (B==F AND B!=D AND F!=H AND E!=I) OR (F==H AND F!=B AND H!=D AND E!=C) => 6=F
 IF H==D AND H!=F AND D!=B => 7=D
 IF (F==H AND F!=B AND H!=D AND E!=G) OR (H==D AND H!=F AND D!=B AND E!=I) => 8=H
 IF F==H AND F!=B AND H!=D => 9=F

Существует также вариант, улучшенный по сравнению с Scale3×, под названием ScaleFX, разработанный Sp00kyFox, и версия, объединенная с Reverse-AA, под названием ScaleFX-Hybrid.

Орел

Eagle работает следующим образом: для каждого входящего пикселя мы сгенерируем 4 исходящих пикселя. Во-первых, установите для всех 4 цвет пикселя, который мы масштабируем в данный момент (как ближайшего соседа). Затем посмотрите на три пикселя сверху, слева и по диагонали сверху слева: если все три имеют один и тот же цвет, установите верхний левый пиксель нашего выходного квадрата на этот цвет, а не на цвет ближайшего соседа. Аналогично поработайте со всеми четырьмя пикселями, а затем переходите к следующему.

Предположим, что входная матрица имеет размер 3 × 3 пикселя, где самый центральный пиксель — это пиксель, подлежащий масштабированию, а выходная матрица — 2 × 2 пикселя (т. е. масштабированный пиксель).

first:        |Then
. . . --\ CC  |S T U  --\ 1 2
. C . --/ CC  |V C W  --/ 3 4
. . .         |X Y Z
              | IF V==S==T => 1=S
              | IF T==U==W => 2=U
              | IF V==X==Y => 3=X
              | IF W==Z==Y => 4=Z

Таким образом, если у нас есть один черный пиксель на белом фоне, он исчезнет. Это ошибка в алгоритме Eagle, но она решается другими алгоритмами, такими как EPX, 2xSaI и HQ2x.

2×SaI

2×SaI , сокращение от 2× Scale and Interpolation engine, было вдохновлено Eagle. Он был разработан Дереком Лиау Ки Фа, также известным как Крид, в первую очередь для использования в консольных и компьютерных эмуляторах , и в этой нише он остается довольно популярным. Многие из самых популярных эмуляторов, включая ZSNES и VisualBoyAdvance , предлагают этот алгоритм масштабирования в качестве функции. Доступно несколько немного отличающихся версий алгоритма масштабирования, их часто называют Super 2×SaI и Super Eagle .

Матрица окружающих пикселей, которую Super2xSaI использует для масштабирования одного пикселя.

Семейство 2xSaI работает с матрицей пикселей 4 × 4 , где масштабируется пиксель, отмеченный буквой A ниже:

I E F J
G A B K --\ W X
H C D L --/ Y Z
M N O P

Для 16-битных пикселей используются маски пикселей, которые изменяются в зависимости от того, равен ли формат 16-битных пикселей 565 или 555. Константы colorMask, lowPixelMask, qColorMask, qLowPixelMask, redBlueMask, и greenMask представляют собой 16-битные маски. Младшие 8 бит идентичны в любом формате пикселей.

Описаны две функции интерполяции:

INTERPOLATE(uint32 A, UINT32 B).
-- linear midpoint of A and B
  if (A == B) return A;
  return (
    ((A & colorMask) >> 1)
  + ((B & colorMask) >> 1)
  + (A & B & lowPixelMask) );

Q_INTERPOLATE(uint32 A, uint32 B, uint32 C, uint32 D)
-- bilinear interpolation; A, B, C, and D's average
  x = ((A & qColorMask) >> 2)
    + ((B & qColorMask) >> 2)
    + ((C & qColorMask) >> 2)
    + ((D & qColorMask) >> 2);
  y = (A & qLowPixelMask)
    + (B & qLowPixelMask)
    + (C & qLowPixelMask)
    + (D & qLowPixelMask);
  y = (y >> 2) & qLowPixelMask;
  return x + y;

Алгоритм проверяет A, B, C и D на диагональное совпадение, такое что A==D и B!=C, или наоборот, или если они обе диагонали, или если совпадения по диагонали нет. Внутри них он проверяет три или четыре одинаковых пикселя. На основе этих условий алгоритм решает, использовать ли один из A, B, C или D или интерполяцию только из этих четырех для каждого выходного пикселя. Произвольный масштабатор 2xSaI может увеличивать любое изображение до любого разрешения и использует билинейную фильтрацию для интерполяции пикселей.

С момента выхода Крида исходный код находится под лицензией GNU General Public License , он доступен бесплатно всем, кто желает использовать его в проекте, выпущенном под этой лицензией. Разработчикам, желающим использовать его в проектах, не подпадающих под GPL, придется переписать алгоритм, не используя какой-либо существующий код Крида.

Он доступен в DosBox через scaler=2xsai вариант.

штаб-квартира n x семья

Основная статья: hqx

Максима Степина hq2x, hq3x и hq4x предназначены для масштабных коэффициентов 2:1, 3:1 и 4:1 соответственно. Каждый из них работает путем сравнения значения цвета каждого пикселя со значениями цвета его восьми непосредственных соседей, маркировки соседей как близких или дальних и использования предварительно созданной таблицы поиска, чтобы найти правильную пропорцию значений входных пикселей для каждого из четырех. 9 или 16 соответствующих выходных пикселей. Семейство hq3x идеально сглаживает любую диагональную линию, наклон которой составляет ±0,5, ±1 или ±2 и которая не сглажена на входе; один с любым другим наклоном будет чередоваться между двумя наклонами на выходе. Это также сгладит очень крутые повороты. В отличие от 2xSaI, он сглаживает выходные данные.

• 
  Изображение увеличено в 3 раза с интерполяцией по ближайшему соседу.
• 
  Изображение увеличено в 3 раза с помощью алгоритма hq3x.

hq n x изначально создавался для Super NES эмулятора ZSNES . Автор bsnes выложил в открытый доступ компактную реализацию hq2x. порт на шейдеры , качество которого сравнимо с ранними версиями xBR. Доступен До порта шейдер под названием «scalehq» часто путали с hqx.

семейство xBR

В этом семействе 6 фильтров: xBR , xBRZ , xBR-Hybrid , Super xBR , xBR+3D и Super xBR+3D .

xBR («масштабирование по правилам»), созданный Хиллианом, работает во многом так же, как HQx (на основе распознавания образов), и будет генерировать тот же результат, что и HQx, при использовании приведенного выше шаблона. Однако он идет дальше, чем HQx, используя двухэтапный набор правил интерполяции , которые лучше обрабатывают более сложные шаблоны, такие как сглаженные линии и кривые. Масштабированные фоновые текстуры сохраняют резкие характеристики исходного изображения, а не размываются, как это делает HQx (на практике часто ScaleHQ). Новейшие версии xBR являются многопроходными и позволяют лучше сохранять мелкие детали. Существует также версия xBR в сочетании с шейдером Reverse-AA под названием xBR-Hybrid. xBR+3D — версия с 3D-маской, которая фильтрует только 2D-элементы.

xBRZ от Zenju — это модифицированная версия xBR. Он реализован с нуля как фильтр на базе ЦП в C++ . Он использует ту же основную идею, что и распознавание и интерполяция образов xBR, но с другим набором правил, предназначенным для сохранения мелких деталей изображения размером всего в несколько пикселей. Это делает его полезным для масштабирования деталей лица и, в частности, глаз. xBRZ оптимизирован для многоядерных процессоров и 64-битных архитектур и показывает производительность на 40–60 % выше, чем HQx, даже при работе только на одном ядре процессора. Он поддерживает масштабирование изображений с помощью альфа-канала и масштабирование целочисленными коэффициентами от 2× до 6×.

Супер xBR — это алгоритм, разработанный Hylian в 2015 году. Он использует некоторые комбинации известных линейных фильтров вместе с правилами обнаружения границ xBR нелинейным образом. Он работает в два прохода и может масштабировать изображение только в два раза (или кратно двум при повторном применении, а также имеет фильтр против звона). Super xBR+3D — версия с 3D-маской, которая фильтрует только 2D-элементы. Существует также версия Super xBR, переписанная на C/C++.

РедСпрайт

Слева: оригинальное пиксельное изображение.
В центре: изображение повернуто с использованием алгоритма вращения ближайшего соседа.
Справа: изображение повернуто с использованием алгоритма RotSprite.

RotSprite — это алгоритм масштабирования и вращения спрайтов, разработанный Xenowhirl. Он создает гораздо меньше артефактов, чем алгоритмы вращения ближайшего соседа, и, как и EPX, не вводит в изображение новые цвета (в отличие от большинства систем интерполяции).

Алгоритм сначала масштабирует изображение в 8 раз по сравнению с его исходным размером с помощью модифицированного алгоритма Scale2×, который рассматривает похожие (а не идентичные) пиксели как совпадения. Затем он (необязательно) вычисляет, какое смещение вращения использовать, отдавая предпочтение точкам выборки, которые не являются граничными пикселями. Затем повернутое изображение создается с помощью алгоритма масштабирования и поворота ближайшего соседа, который одновременно сжимает большое изображение до исходного размера и поворачивает изображение. Наконец, пропущенные однопиксельные детали (необязательно) восстанавливаются, если соответствующий пиксель в исходном изображении отличается, а целевой пиксель имеет трех одинаковых соседей.

Быстрый РедСпрайт

Fast RotSprite — это алгоритм быстрого вращения пиксельной графики, разработанный Олегом Мекекечко для приложения Pixel Studio . Он основан на RotSprite , но имеет лучшую производительность с небольшой потерей качества. Он может обрабатывать большие изображения в режиме реального времени. Вместо 8-кратного повышения качества Fast RotSprite использует одно 3-кратное повышение разрешения. Затем он просто поворачивает все пиксели с округлением координат. Наконец, он уменьшает масштаб в 3 раза без введения новых цветов. Поскольку все операции на каждом этапе независимы, их можно выполнять параллельно, что значительно повышает производительность.

Копф-Лишински

Алгоритм Копфа-Лищинского — это новый способ извлечения независимой от разрешения векторной графики из пиксельной графики, описанный в статье 2011 года «Депикселизация пиксельной графики». Доступна реализация Python.

Алгоритм был перенесен на графические процессоры и оптимизирован для рендеринга в реальном времени. Исходный код доступен для этого варианта.

Интерполяция по краям (EDI)

Интерполяция по краям (EDI) описывает методы масштабирования, в которых используется статистическая выборка для обеспечения качества изображения при его масштабировании. Существовало несколько более ранних методов, которые включали обнаружение краев для генерации весов смешивания для линейной интерполяции или классификации пикселей в соответствии с условиями их соседства и использования различных схем изотропной интерполяции, основанных на классификации. Любой данный подход интерполяции сводится к средневзвешенным значениям соседних пикселей. Цель – найти оптимальные веса. Билинейная интерполяция устанавливает все веса равными. Методы интерполяции более высокого порядка, такие как бикубическая или синк-интерполяция, учитывают большее количество соседей, чем только соседние.

ВНИЗ

NEDI (новая интерполяция, направленная на края) вычисляет локальные ковариации исходного изображения и использует их для адаптации интерполяции с высоким разрешением. Это прототип фильтра этого семейства.

EDIUpsizer

EDIUpsizer — это фильтр передискретизации, который изменяет размер изображения в два раза как по горизонтали, так и по вертикали с использованием NEDI (новая интерполяция, направленная по краям). EDIUpsizer также использует несколько модификаций базового NEDI, чтобы предотвратить появление множества артефактов, которые NEDI создает в детальных областях. К ним относятся тестирование числа условий и адаптивный размер окна, а также ограничение ограничений. Все модификации и ограничения NEDI являются необязательными (их можно включать и выключать) и настраиваются пользователем. Этот фильтр довольно медленный.

FastEDIUpsizer

FastEDIUpsizer — это уменьшенная версия EDIUpsizer, немного более настроенная на скорость. Он использует постоянный размер окна 8 × 8 , выполняет NEDI только на плоскости яркости и использует только бикубическую или билинейную интерполяцию в качестве резервного метода интерполяции.

eedi3

Еще один интерполяционный фильтр, ориентированный на края. Работает путем минимизации функции стоимости, включающей каждый пиксель в строке сканирования. Это медленно.

EEDI2

EEDI2 изменяет размер изображения в 2 раза по вертикали, копируя существующее изображение в 2⋅y(n) и интерполируя отсутствующее поле. Он предназначен для интерполяции по краям для деинтерлейсинга (т.е. не предназначен для изменения размера обычного изображения, но тоже может это делать). EEDI2 можно использовать как с TDeint, так и с TIVTC; дополнительную информацию о том, как это сделать, см. по ссылке обсуждения.

СуперРазрешение

СуперРес шейдеры используют другой метод масштабирования, который можно использовать в сочетании с NEDI (или любым другим алгоритмом масштабирования). Этот метод подробно описан его создателем Шиандоу в сообщении на форуме Doom9 в 2014 году. Этот метод часто дает лучшие результаты, чем просто использование NEDI, и конкурирует с NNEDI3. Теперь они также доступны в виде сценария рендеринга MPDN.

НИЧЕГО

NNEDI — это семейство внутриполевых деинтерлейсеров , которые также можно использовать для увеличения изображений в степени двойки. При использовании в качестве деинтерлейсера он принимает кадр , отбрасывает одно поле , а затем интерполирует недостающие пиксели, используя только информацию из сохраненного поля. На данный момент существует три основных поколения NNEDI.

NNEDI, оригинальная версия, работает со YUY2 и YV12 . входами В NNEDI2 добавлена ​​поддержка RGB24 и специальная функция. nnedi2_rpow2 для масштабирования. предиктора NNEDI3 расширяет NNEDI2 с помощью нейронной сети- . И размер сети, и район, который она исследует, можно настроить для достижения компромисса между скоростью и качеством:

Это соотношение качества и скорости; однако различия между количеством нейронов для определенного коэффициента изменения размера обычно невелики, однако разница в производительности между количеством нейронов становится больше, когда вы увеличиваете размер изображения в четыре раза. Если вы планируете удвоить разрешение, вы не увидите огромной разницы между 16 и 256 нейронами. Между самым высоким и самым низким вариантами все еще существует заметная разница, но разница не на порядки.

См. также

• libretro — реализует многие вышеупомянутые алгоритмы в виде шейдеров.
• Pixelscalers — реализации C++ алгоритмов ScaleNx, hqNx и superXBR в отдельном инструменте.