Рассечение на ортосхемы

Нерешенная задача по математике :

Можно ли любой симплекс разбить на ограниченное число ортосхем?

В геометрии это нерешенная гипотеза о Хьюго Хадвигера том, что каждый симплекс можно разбить на ортосхемы , используя количество ортосхем, ограниченное функцией размерности симплекса. ^[1] Если это правда, то в более общем смысле каждый выпуклый многогранник можно разбить на ортосхемы.

Определения и заявление

В этом контексте симплекс в $d$ -мерное евклидово пространство — это выпуклая оболочка $d+1$ точки, не все лежащие в одной гиперплоскости . Например, 2-мерный симплекс — это просто треугольник ( выпуклая оболочка из трех точек на плоскости), а 3-мерный симплекс — это тетраэдр (выпуклая оболочка из четырех точек в трехмерном пространстве). Точки, образующие таким образом симплекс, называются его вершинами .

Ортосхема, также называемая симплексом путей, представляет собой особый вид симплекса. В нем вершины могут быть соединены путем так , что каждые два ребра пути расположены под прямым углом друг к другу. Двумерная ортосхема представляет собой прямоугольный треугольник . Трехмерную ортосхему можно построить из куба, найдя путь из трех ребер куба, которые не все лежат на одной квадратной грани, и образовав выпуклую оболочку из четырех вершин на этом пути.

Рассечение формы $S$ (которое может быть любым замкнутым множеством в евклидовом пространстве) является представлением $S$ как союз других фигур, внутренности которых не пересекаются друг с другом . То есть интуитивно фигуры в объединении не перекрываются, хотя на своих границах могут иметь общие точки. Например, куб можно разбить на шесть трехмерных ортосхем. Аналогичный результат применим и в более общем плане: каждый гиперкуб или гиперпрямоугольник в $d$ размеры можно разделить на $d!$ ортосхемы.

Гипотеза Хадвигера состоит в том, что существует функция $f$ такой, что каждый $d$ -мерный симплекс можно разбить не более чем на $f(d)$ ортосхемы. Хадвигер поставил эту проблему в 1956 году; ^[2] в общем случае она остается нерешенной, хотя есть и частные случаи для малых значений $d$ известны. ^[1]

В небольших размерах

Высота под острым углом может не рассечь треугольник, но высота под самым широким углом всегда рассекает его на два прямоугольных треугольника.

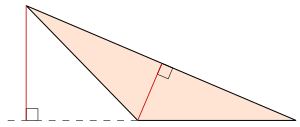
В двух измерениях каждый треугольник можно разрезать не более чем на два прямоугольных треугольника, опустив высоту от самого широкого угла к самому длинному краю. ^[2]

В трех измерениях некоторые тетраэдры можно разрезать аналогичным образом, опустив высоту перпендикулярно вершине. $v$ в точку $p$ в противоположном лице, соединяя $p$ перпендикулярно сторонам лица и используя трехгранные перпендикулярные пути через $v$ и $p$ в сторону, а затем в вершину лица. ^[2] Однако это не всегда работает. В частности, существуют тетраэдры, у которых ни одна из вершин не имеет высоты со ногой внутри противоположной грани.Используя более сложную конструкцию, Ленхард (1960) доказал, что каждый тетраэдр можно разбить не более чем на 12 ортосхем. ^[3]Бём (1980) доказал, что это оптимально: существуют тетраэдры, которые нельзя разбить менее чем на 12 ортосхем. ^[4] В той же статье Бём также обобщил результат Ленхарда на трёхмерную сферическую геометрию и трёхмерную гиперболическую геометрию .

В четырех измерениях необходимо не более 500 ортосхем. ^[5] В пяти измерениях снова необходимо конечное число ортосхем, примерно не более 12,5 миллионов. Опять же, это относится к сферической геометрии и гиперболической геометрии, а также к евклидовой геометрии. ^[6]

Гипотеза Хадвигера остается недоказанной для всех размерностей больше пяти. ^[1]

Последствия

Любой выпуклый многогранник можно разбить на симплексы. Следовательно, если гипотеза Хадвигера верна, каждый выпуклый многогранник также будет расщепляться на ортосхемы. ^[6]

Связанный с этим результат состоит в том, что каждая ортосхема сама по себе может быть разделена на $d$ или $d+1$ ортосхемы меньшего размера. ^[7]^[8] Поэтому для симплексов, которые можно разбить на ортосхемы, их разрезы могут иметь сколь угодно большое число ортосхем.

Ссылки

^ Jump up to: Перейти обратно: ^а ^б ^с Брандтс, Ян; Коротов Сергей; Кржижек, Михал; Шольц, Якуб (2009), «О нетупых симплициальных разбиениях» (PDF) , SIAM Review , 51 (2): 317–335, doi : 10.1137/060669073 , MR 2505583 . См., в частности, Гипотезу 23, с. 327.
^ Jump up to: Перейти обратно: ^а ^б ^с Хадвигер, Хьюго (1956), «Нерешенные проблемы» , «Элементы математики» , 11 : 109–110.
^ Ленхард, Х.-Хр. (1960), "Разложение тетраэдров на ортогональные тетраэдры" , Элементы математики , 15 : 106–107, МР 0116226
^ Бём, Йоханнес (1980), «О полном разложении евклидовых и неевклидовых тетраэдров в ортогональные тетраэдры», Университет Мартина Лютера Галле-Виттенберг (9): 29–54, MR 0579516
^ Чирпке, Катрин (1993), «О расчленении симплексов на ортосхемы», Geometriae Dedicata 46 ( 3):313–329, doi : 10.1007/BF01263622 , MR1220122 ,
^ Jump up to: Перейти обратно: ^а ^б Чирпке, Катрин (1994), «Разбиение пятимерных симплексов на ортосхемы» , Вклад в алгебру и геометрию , 35 (1): 1–11, MR 1287191
^ Дебруннер, Ханс Э. (1990), «Разбиение ортосхем на ортосхемы», Applied Geometry , 33 (2): 123–152, doi : 10.1007/BF00183080 , MR 1050606
^ Брандтс, Ян; Коротов Сергей; Кржижек, Михал (2007), "Рассечение пути-симплекса в $\mathbb {R} ^{n}$ в $n$ пути-подсимплексы», Линейная алгебра и ее приложения , 421 (2–3): 382–393, doi : 10.1016/j.laa.2006.10.010 , MR 2294350

[bkks-1] Jump up to: Перейти обратно: ^а ^б ^с Брандтс, Ян; Коротов Сергей; Кржижек, Михал; Шольц, Якуб (2009), «О нетупых симплициальных разбиениях» (PDF) , SIAM Review , 51 (2): 317–335, doi : 10.1137/060669073 , MR 2505583 . См., в частности, Гипотезу 23, с. 327.

[hh-2] Jump up to: Перейти обратно: ^а ^б ^с Хадвигер, Хьюго (1956), «Нерешенные проблемы» , «Элементы математики» , 11 : 109–110.

[len-3] Ленхард, Х.-Хр. (1960), "Разложение тетраэдров на ортогональные тетраэдры" , Элементы математики , 15 : 106–107, МР 0116226

[bohm-4] Бём, Йоханнес (1980), «О полном разложении евклидовых и неевклидовых тетраэдров в ортогональные тетраэдры», Университет Мартина Лютера Галле-Виттенберг (9): 29–54, MR 0579516

[tschirpke93-5] Чирпке, Катрин (1993), «О расчленении симплексов на ортосхемы», Geometriae Dedicata 46 ( 3):313–329, doi : 10.1007/BF01263622 , MR1220122 ,

[tschirpke94-6] Jump up to: Перейти обратно: ^а ^б Чирпке, Катрин (1994), «Разбиение пятимерных симплексов на ортосхемы» , Вклад в алгебру и геометрию , 35 (1): 1–11, MR 1287191

[debrunner-7] Дебруннер, Ханс Э. (1990), «Разбиение ортосхем на ортосхемы», Applied Geometry , 33 (2): 123–152, doi : 10.1007/BF00183080 , MR 1050606

[bkk-8] Брандтс, Ян; Коротов Сергей; Кржижек, Михал (2007), "Рассечение пути-симплекса в $\mathbb {R} ^{n}$ в $n$ пути-подсимплексы», Линейная алгебра и ее приложения , 421 (2–3): 382–393, doi : 10.1016/j.laa.2006.10.010 , MR 2294350

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]