Концептуальное письмо
 Титульный лист оригинального издания 1879 года. | |
| Автор | Слава Богу, Фреге |
|---|---|
| Язык | Английский |
| Жанр | Логика |
| Издатель | Любрехт и Крамер |
Дата публикации | 1879 |
| Страницы | 124 |
| ISBN | 978-3487-0062-39 |
| ОКЛК | 851287 |
Begriffsschrift (по-немецки грубо говоря «написание концепций») — это книга Готлоба Фреге по опубликованная логике , в 1879 году, и формальная система, изложенная в этой книге.
Begriffsschrift обычно переводится как написание концепций или обозначение концепций ; полное название книги определяет ее как « формул язык , созданный по образцу арифметического языка для чистого мышления ». Мотивация Фреге к разработке формального подхода к логике напоминала рационализатора мотивацию Лейбница для его исчисления (несмотря на это, в предисловии Фреге явно отрицает, что он достиг этой цели, а также то, что его главной целью было бы построение идеального языка, подобного языку Лейбница, который Фреге заявляет, что это довольно трудная и идеалистическая, хотя и не невыполнимая задача). Фреге продолжал использовать свои логические расчеты в своих исследованиях основ математики , проводившихся в течение следующей четверти века. Это первая работа в области аналитической философии , области, которую впоследствии развили будущие британские и англоязычные философы, такие как Бертран Рассел .
Обозначения и система
[ редактировать ]Исчисление впервые содержит количественные переменные и, по сути, представляет собой классическую двухвалентную логику второго порядка с единицей. Он двухвалентен в том смысле, что предложения или формулы обозначают либо Истину, либо Ложь; второго порядка, поскольку он включает переменные отношения в дополнение к переменным объекта и позволяет количественно оценить обе. Модификатор «с идентичностью» указывает, что язык включает отношение идентичности =. Фреге заявил, что его книга представляет собой версию «Characterica Universalis» , концепции Лейбница, которая будет применяться в математике. [1]
Фреге представляет свое исчисление, используя своеобразную двумерную запись : связки и кванторы записываются с помощью линий, соединяющих формулы, а не символов ¬, ∧ и ∀, которые используются сегодня. Например, суждение B существенно подразумевает суждение A , т.е. написано как ![]() .
.
В первой главе Фреге определяет основные идеи и обозначения, такие как предложение («суждение»), квантор всеобщности («общность»), условное выражение , отрицание и «знак тождества содержания». (которое он использовал для обозначения как материальной эквивалентности , так и собственно тождества); во второй главе он объявляет девять формализованных предложений аксиомами.
| Основная концепция | Обозначения Фреге | Современные обозначения |
|---|---|---|
| Судить | ||
| Отрицание | ||
| Условное (подразумевается) |  | |
| Универсальная количественная оценка | ||
| Экзистенциальная количественная оценка | ||
| Идентичность контента (эквивалентность/идентичность) |
В главе 1, §5 Фреге определяет условное выражение следующим образом:
- «Пусть A и B относятся к оцениваемому содержанию, тогда четыре возможности таковы:
- Утверждается А, утверждается Б;
- А утверждается, Б отрицается;
- A отрицается, B утверждается;
- А отрицается, Б отрицается.
Позволять
означают, что третья из этих возможностей не реализуется, но реализуется одна из трех других. Итак, если мы отрицаем  , это означает, что справедлива третья возможность, т. е. мы отрицаем А и утверждаем Б».
, это означает, что справедлива третья возможность, т. е. мы отрицаем А и утверждаем Б».
Исчисление в работах Фреге
[ редактировать ]Фреге объявил девять своих положений аксиомами и оправдал их, неформально утверждая, что, учитывая их предполагаемое значение, они выражают самоочевидные истины. Эти аксиомы, выраженные в современных обозначениях, таковы:
Это предложения 1, 2, 8, 28, 31, 41, 52, 54 и 58 в Begriffschrifft . (1)–(3) управляют материальной импликацией , (4)–(6) отрицанием , (7) и (8) идентичностью и (9) универсальным квантором . (7) выражает , Лейбница неразличимость тождеств а (8) утверждает, что тождество является рефлексивным отношением .
Все остальные предложения выводятся из (1)–(9) путем применения любого из следующих правил вывода :
- Метод установки позволяет сделать вывод от и ;
- Правило обобщения позволяет сделать вывод от если x не встречается в P ;
- Правило замены , которое Фреге не формулирует явно. Это правило гораздо сложнее сформулировать точно, чем два предыдущих правила, и Фреге ссылается на него способами, которые не являются очевидно законными.
Основные результаты третьей главы, озаглавленной «Части общей теории рядов», касаются того, что сейчас предком отношения R. называют « a является R -предком b » пишется « aR * b ».
Фреге применил результаты Begriffsschrifft , в том числе результаты о предках отношения, в своей более поздней работе «Основы арифметики» . Таким образом, если мы возьмем xRy за отношение y = x + 1, то 0 R * y будет предикатом « y — натуральное число». (133) говорит, что если x , y и z — натуральные числа , то должно выполняться одно из следующих условий: x < y , x = y или y < x . Это так называемый «закон трихотомии ».
Влияние на другие произведения
[ редактировать ]Недавнее тщательное исследование того, как Begriffsschrift рассматривалось в немецкой математической литературе, см. в Vilko (1998). Некоторые рецензенты, особенно Эрнст Шредер , в целом отнеслись к нему положительно. Все работы в области формальной логики, последовавшие за Begriffsschrift, обязаны ему, потому что его логика второго порядка была первой формальной логикой, способной представить изрядную часть математики и естественного языка.
Некоторые остатки обозначений Фреге сохранились в символе « турникета ». происходит от его «Urteilsstrich» ( судящий/выводящий штрих ) │ и «Inhaltsstrich» (т.е. содержательный штрих ) ──. Фреге использовал эти символы в Begriffsschrift в унифицированной форме ├─ для заявления об истинности предложения. В своей более поздней «Grundgesetze» он немного пересматривает свою интерпретацию символа ├─.
В «Begriffsschrift» «Definitionsdoppelstrich» (т.е. двойная черта определения ) │├─ указывает на то, что предложение является определением. Кроме того, знак отрицания можно прочитать как комбинацию горизонтального Inhaltsstrich с вертикальным штрихом отрицания. Этот символ отрицания был вновь введен Арендом Хейтингом. [2] в 1930 году, чтобы отличить интуиционистское отрицание от классического. Он также появляется в докторской диссертации Герхарда Генцена .
В «Логическом философском трактате» Людвиг Витгенштейн отдает дань уважения Фреге, используя термин Begriffsschrift как синоним логического формализма.
В эссе Фреге 1892 года « О смысле и референции » отрекаются от некоторых выводов Begriffsschrifft об идентичности (обозначаемых в математике знаком «=»). В частности, он отвергает точку зрения «Begriffsschrift», согласно которой предикат идентичности выражает связь между именами, в пользу заключения, что он выражает связь между объектами , обозначаемыми этими именами.
Издания
[ редактировать ]- Слава Богу, Фреге . Концептуальное письмо: формульный язык чистого мышления, основанный на арифметике . Галле-ан-дер-Заале: издательство Луи Неберта, 1879 г.
Переводы:
- Байнум, Террелл Уорд , переведено и отредактировано, 1972. Концептуальные обозначения и связанные статьи с биографией и введением. Издательство Оксфордского университета .
- Бауэр-Менгельберг, Стефан, 1967, «Концептуальный сценарий» в книге Жана ван Хейеноорта , изд., От Фреге до Гёделя: Справочник по математической логике, 1879–1931 . Издательство Гарвардского университета .
- Бини, Майкл, 1997, «Begriffsschrift: Selections (предисловие и часть I)» в The Frege Reader . Оксфорд: Блэквелл.
См. также
[ редактировать ]- Родовые отношения
- Исчисление эквивалентных утверждений
- Логика первого порядка
- Исчисление высказываний Фреге
- Предварительная аналитика
- Законы мышления
- Принципы математики
Ссылки
[ редактировать ]- ^ Корте, Тапио (22 октября 2008 г.). «Концептуальное письмо Фреге как характеристика языка» . Синтез . 174 (2): 283–294. дои : 10.1007/s11229-008-9422-7 . S2CID 20587814 .
- ^ Аренд Хейтинг: «Формальные правила интуиционистской логики», в: Труды Прусской академии наук, физико-математический класс , 1930, стр. 42–65.
Библиография
[ редактировать ]- Джордж Булос , 1985. «Чтение концептуального письма », Mind 94: 331–344.
- Айвор Граттан-Гиннесс , 2000. В поисках математических корней . Издательство Принстонского университета.
- Ристо Вилкко, 1998, « Фреге Прием Wortschrift », Historia Mathematica 25 (4) : 412–422.
Внешние ссылки
[ редактировать ]- Залта, Эдвард Н. «Логика, теорема и основы арифметики Фреге» . В Залте, Эдвард Н. (ред.). Стэнфордская энциклопедия философии .
- Концептуальный документ в виде факсимиле для скачивания (2,5 МБ)
- Эзотерический язык программирования : «Готтлоб: написание кода в концептуальной нотации Фреге» . эзотерические.коды . 27 марта 2020 г. Проверено 19 июня 2022 г.













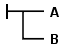

![{\displaystyle \vdash \ \ \ left [\ A \ rightarrow \ left (B \ rightarrow C \ right) \ \ right] \ \ rightarrow \ \ left [\ \ left (A \ rightarrow B \ right) \ rightarrow \ left (A\rightarrow C\right)\ \right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/46233b0b84387b488948fe5ad59cef954c68fc83)
![{\displaystyle \vdash \ \ \ left [\ D \ rightarrow \ left (B \ rightarrow A \ right) \ \ right] \ \ rightarrow \ \ left [\ B \ rightarrow \ left (D \ rightarrow A \ right) \ \верно]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fdf8f5830ad951a8c528ea7eec78a90a79a61594)












