Воздушный диск

Созданный компьютером образ диска Эйри. Интенсивность оттенков серого была отрегулирована для повышения яркости внешних колец узора Эйри.

Диск Эйри, созданный компьютером из дифрагированного белого света ( спектр D65 ). Обратите внимание, что красный компонент преломляется сильнее, чем синий, поэтому центр кажется слегка голубоватым.

Настоящий диск Эйри, созданный путем пропускания красного лазерного луча через точечную апертуру диаметром 90 микрометров с дифракцией 27 порядков.

Диск Эйри, снятый объективом камеры с фокусным расстоянием 2000 мм и диафрагмой f/25. Размер изображения: 1×1 мм.

В оптике диск Эйри (или диск Эйри ) и узор Эйри это описания наиболее сфокусированного пятна светового — , которое может создать идеальная линза с круглой апертурой , ограниченная дифракцией света. Диск Эйри имеет важное значение в физике , оптике и астрономии .

Дифракционная картина, возникающая в результате равномерно освещенной круглой апертуры, имеет яркую центральную область , известную как диск Эйри, которая вместе с серией концентрических колец вокруг называется картиной Эйри. Оба названы в честь Джорджа Бидделла Эйри . Феномен диска и колец был известен до Эйри; Джон Гершель описал внешний вид яркой звезды , увиденной в телескоп при сильном увеличении, в статье о свете 1828 года для Энциклопедии Метрополитана :

... тогда звезда видится (при благоприятных условиях спокойной атмосферы, однородной температуры и т. д.) как совершенно круглый, четко выраженный планетарный диск, окруженный двумя, тремя или более попеременно темными и яркими кольцами, которые, если при внимательном рассмотрении видно, что их границы слегка окрашены. Они следуют друг за другом почти через равные промежутки вокруг центрального диска...

Эйри написал первое полное теоретическое исследование, объясняющее это явление (его работа «О дифракции в объективе с круглой апертурой», 1835 г.).

Математически дифракционная картина характеризуется длиной волны света, освещающего круглую апертуру, и размером апертуры. Внешний вид дифракционной картины дополнительно характеризуется чувствительностью глаза или другого детектора, используемого для наблюдения картины.

Наиболее важным применением этой концепции являются камеры , микроскопы и телескопы . Из-за дифракции наименьшая точка, в которую линза или зеркало может сфокусировать луч света, имеет размер диска Эйри. Даже если бы удалось создать идеальный объектив, все равно существует предел разрешения изображения, создаваемого таким объективом. Оптическая система, в которой разрешение больше не ограничивается несовершенством линз, а только дифракцией, называется ограниченной дифракцией .

Размер

Вдали от апертуры угол, при котором возникает первый минимум, отсчитываемый от направления падающего света, определяется приближенной формулой:

$$\sin \theta \approx 1.22{\frac {\lambda }{d}}$$

или, для малых углов, просто

$$\theta \approx 1.22{\frac {\lambda }{d}},$$

где $\theta$ находится в радианах, $\lambda$ длина волны света в метрах, а ${d}$ — диаметр проема в метрах. Полная ширина на половине высоты определяется выражением $\theta _{\mathrm {FWHM} }=1.029{\frac {\lambda }{d}}.$

Эйри записал это соотношение как

$$s={\frac {2.76}{a}},$$

где ${s}$ был угол первого минимума в угловых секундах, ${a}$ был радиус апертуры в дюймах, а длина волны света предполагалась равной 0,000022 дюйма (560 нм; среднее значение видимых длин волн). Это равно угловому разрешению круглой апертуры. Критерий Рэлея для едва разрешения двух объектов, которые являются точечными источниками света, таких как звезды, видимые в телескоп, заключается в том, что центр диска Эйри для первого объекта находится в первом минимуме диска Эйри второго. Это означает, что угловое разрешение дифракционно-ограниченной системы определяется теми же формулами.

Однако, хотя угол, при котором возникает первый минимум (который иногда называют радиусом диска Эйри), зависит только от длины волны и размера апертуры, внешний вид дифракционной картины будет меняться в зависимости от интенсивности (яркости) источника света. . Поскольку любой детектор (глазной, пленочный, цифровой), используемый для наблюдения дифракционной картины, может иметь порог интенсивности обнаружения, полная дифракционная картина может быть не видна. В астрономии внешние кольца часто не видны даже на сильно увеличенном изображении звезды. Возможно, ни одно из колец не видно, и в этом случае изображение звезды выглядит как диск (только центральный максимум), а не как полная дифракционная картина. Кроме того, более тусклые звезды будут выглядеть как диски меньшего размера, чем более яркие звезды, поскольку меньшая часть их центрального максимума достигает порога обнаружения. Хотя теоретически все звезды или другие «точечные источники» данной длины волны и видимые через данную апертуру имеют одинаковый радиус диска Эйри, характеризуемый приведенным выше уравнением (и одинаковый размер дифракционной картины), отличающийся только интенсивностью, внешний вид таков, что более слабые источники выглядят как диски меньшего размера, а более яркие источники выглядят как диски большего размера. Это описал Эйри в своей оригинальной работе:

Быстрое уменьшение света в последовательных кольцах вполне объяснит видимость двух-трех колец с очень яркой звездой и невидимость колец со слабой звездой. Различие диаметров центральных пятен (или ложных дисков) разных звезд… также вполне объяснено. Так, радиус ложного диска слабой звезды, где свет менее половины интенсивности центрального света не производит впечатления на глаз, определяется [ s = 1,17/ a ], тогда как радиус ложного диска яркая звезда, для которой ощутим свет, равный 1/10 интенсивности центрального света, определяется соотношением [ s = 1,97/ a ].

Несмотря на эту особенность работы Эйри, даже в стандартных учебниках радиус диска Эйри часто называют просто углом первого минимума. В действительности угол первого минимума является предельной величиной размера диска Эйри, а не определенным радиусом.

Примеры

Логарифмический график зависимости диаметра апертуры от углового разрешения на дифракционном пределе для различных длин волн света по сравнению с различными астрономическими инструментами. Например, синяя звезда показывает, что космический телескоп Хаббл почти дифракционно ограничен в видимом спектре на уровне 0,1 угловой секунды, тогда как красный кружок показывает, что человеческий глаз теоретически должен иметь разрешающую способность 20 угловых секунд, хотя зрение 20/20. разрешается только до 60 угловых секунд (1 угловая минута)

Камеры

Если два объекта, изображенные камерой, разделены настолько малым углом, что их диски Эйри на детекторе камеры начинают перекрываться, объекты больше не могут быть четко разделены на изображении, и они начинают стираться вместе. Говорят, что два объекта только что решены , когда максимум первого шаблона Эйри попадает на вершину первого минимума второго шаблона Эйри ( критерий Рэлея ).

Следовательно, наименьшее угловое расстояние, которое могут иметь два объекта до того, как они значительно размываются друг с другом, определяется, как указано выше, выражением $$\sin \theta =1.22\,{\frac {\lambda }{d}}.$$

Таким образом, способность системы разрешать детали ограничена соотношением λ/ d . Чем больше апертура для данной длины волны, тем более мелкие детали можно различить на изображении.

Это также можно выразить как $${\frac {x}{f}}=1.22\,{\frac {\lambda }{d}},$$ где $x$ - это разделение изображений двух объектов на пленке, и $f$ расстояние от линзы до пленки. Если принять расстояние от линзы до пленки примерно равным фокусному расстоянию линзы, то найдем $$x=1.22\,{\frac {\lambda \,f}{d}},$$ но ${\frac {f}{d}}$ это f-число объектива. Типичная настройка для использования в пасмурный день: f /8 (см. правило Санни 16 ). Для фиолетового, видимого света с самой короткой длиной волны, длина волны λ составляет около 420 нанометров ( см чувствительность S-конусных ячеек . в разделе «Колбочки»). Это дает значение для $x$ около 4 мкм. В цифровой камере уменьшение размера пикселей датчика изображения вдвое меньше этого значения (по одному пикселю для каждого объекта, по одному на каждое пространство между ними) не приведет к значительному увеличению разрешения захватываемого изображения . Однако это может улучшить окончательное изображение за счет передискретизации, что позволит снизить шум.

Человеческий глаз

Продольные сечения сфокусированного луча с отрицательной (вверху), нулевой (в центре) и положительной сферической аберрацией (внизу). Объектив находится слева.

Самое быстрое число f для человеческого глаза составляет около 2,1. что соответствует ограниченной дифракцией функции рассеяния точки диаметром примерно 1 мкм. Однако при этом числе f сферическая аберрация ограничивает остроту зрения, а диаметр зрачка 3 мм (f/5,7) приближается к разрешению, достигаемому человеческим глазом. Максимальная плотность колбочек в фовеа человека составляет примерно 170 000 на квадратный миллиметр. это означает, что расстояние между колбочками в человеческом глазу составляет около 2,5 мкм, что примерно соответствует диаметру функции рассеяния точки при f/5.

Сфокусированный лазерный луч

Круговой лазерный луч с одинаковой интенсивностью по всему кругу (луч с плоской вершиной), сфокусированный линзой, образует в фокусе узор диска Эйри. Размер диска Эйри определяет интенсивность лазера в фокусе.

Прицельный прицел

Некоторые прицелы для прицеливания оружия (например, FN FNC ) требуют от пользователя совмещения прицела (заднего, ближнего прицела, т. е. который будет не в фокусе) с наконечником (который должен быть сфокусирован и наложен на цель) в конце прицела. бочка. Глядя в прицел, пользователь заметит диск Эйри, который помогает центрировать прицел над штифтом.

Условия для наблюдения

Свет из равномерно освещенной круглой апертуры (или от однородного луча с плоской вершиной) будет демонстрировать дифракционную картину Эйри вдали от апертуры из-за дифракции Фраунгофера (дифракции в дальнем поле).

Условия нахождения в дальнем поле и проявления диаграммы Эйри таковы: падающий свет, освещающий апертуру, представляет собой плоскую волну (нет изменения фазы в апертуре), интенсивность постоянна по площади апертуры, а расстояние $R$ расстояние от апертуры, где наблюдается дифрагированный свет (расстояние до экрана), велико по сравнению с размером апертуры, а радиус $a$ апертуры не намного больше длины волны $\lambda$ света. Последние два условия формально можно записать как $R>a^{2}/\lambda .$

На практике условия равномерного освещения можно обеспечить, разместив источник освещения вдали от апертуры. Если условия для дальнего поля не соблюдаются (например, если апертура большая), дифракционную картину Эйри в дальнем поле можно также получить на экране, намного ближе к апертуре, используя линзу сразу после апертуры (или линзу сам может образовывать апертуру). Тогда узор Эйри будет формироваться в фокусе линзы, а не на бесконечности.

Следовательно, фокусное пятно однородного кругового лазерного луча (луча с плоской вершиной), сфокусированного линзой, также будет представлять собой узор Эйри.

В камере или системе формирования изображения объект, находящийся далеко, отображается на пленке или плоскости детектора с помощью объектива, и на детекторе наблюдается картина дифракции в дальнем поле. Полученное изображение представляет собой свертку идеального изображения с дифракционной картиной Эйри из-за дифракции на диафрагме или из-за конечного размера линзы. Это приводит к конечному разрешению системы линз, описанной выше.

Математическая формулировка

Дифракция от круглого отверстия. Модель Эйри наблюдается, когда $R\gg a^{2}/\lambda$ (то есть в дальнем поле)

Дифракция от апертуры с линзой. Изображение в дальнем поле будет (только) формироваться на экране на расстоянии одного фокусного расстояния, где R=f (f=фокусное расстояние). Угол наблюдения $\theta$ остается таким же, как и в безлинзовом футляре.

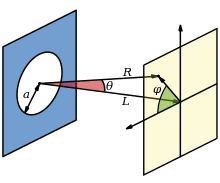
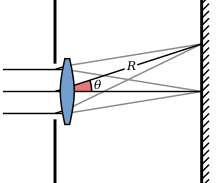
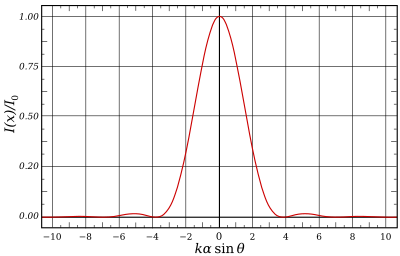
Интенсивность круглого отверстия узора Эйри соответствует дифракционной картине Фраунгофера , определяемой квадратом модуля преобразования Фурье круглого отверстия:

$$I(\theta )=I_{0}\left[{\frac {2J_{1}(k\,a\sin \theta )}{k\,a\sin \theta }}\right]^{2}=I_{0}\left[{\frac {2J_{1}(x)}{x}}\right]^{2}$$

где $I_{0}$ — максимальная интенсивность рисунка в центре диска Эйри, $J_{1}$ – функция Бесселя первого рода порядка, $k={2\pi }/{\lambda }$ волновое число, $a$ - радиус апертуры, а $\theta$ – угол наблюдения, т.е. угол между осью круглого отверстия и линией между центром отверстия и точкой наблюдения. $x=ka\sin \theta ={\frac {2\pi a}{\lambda }}{\frac {q}{R}},$ где q — радиальное расстояние от точки наблюдения до оптической оси, R — расстояние до апертуры. Обратите внимание, что диск Эйри, заданный приведенным выше выражением, действителен только для больших R , где дифракция Фраунгофера применяется ; расчет тени в ближнем поле скорее следует производить с использованием дифракции Френеля .

Однако точный узор Эйри действительно появляется на конечном расстоянии, если линзу поместить в апертуру. Тогда узор Эйри будет идеально сфокусирован на расстоянии, определяемом фокусным расстоянием линзы (при условии, что коллимированный свет падает на апертуру), определяемом приведенными выше уравнениями.

Нули $J_{1}(x)$ находятся в $x=ka\sin \theta \approx 3.8317,7.0156,10.1735,13.3237,16.4706\dots .$ Отсюда следует, что первое темное кольцо на дифракционной картине возникает там, где $ka\sin {\theta }=3.8317\dots ,$ или

$$\sin \theta \approx {\frac {3.83}{ka}}={\frac {3.83\lambda }{2\pi a}}=1.22{\frac {\lambda }{2a}}=1.22{\frac {\lambda }{d}}.$$

Если линза используется для фокусировки узора Эйри на конечном расстоянии, то радиус $q_{1}$ первого темного кольца в фокальной плоскости определяется исключительно числовой апертурой A (тесно связанной с числом f ) выражением $$q_{1}=R\sin \theta _{1}\approx 1.22{R}{\frac {\lambda }{d}}=1.22{\frac {\lambda }{2A}}$$

где числовая апертура A равна радиусу апертуры d /2, деленному на R', расстояние от центра диаграммы Эйри до края апертуры. Рассматривая апертуру радиуса d /2 и линзу как камеру (см. диаграмму выше), проецирующую изображение на фокальную плоскость на расстоянии f , числовая апертура A связана с широко цитируемым f-числом N = f/d (отношение фокусного расстояния к диаметру линзы) согласно

$$A={\frac {r}{R'}}={\frac {r}{\sqrt {f^{2}+r^{2}}}}={\frac {1}{\sqrt {4N^{2}+1}}};$$

для N ≫1 он просто аппроксимируется как ${\textstyle A\approx 1/2N.}$ Это показывает, что наилучшее возможное разрешение изображения камеры ограничено числовой апертурой (и, следовательно, числом f) ее объектива из-за дифракции .

Половина максимума центрального диска Эйри (где $2J_{1}(x)/x=1/{\sqrt {2}}$) происходит при $x=1.61633995\dots ;$ 1/е ² точка (где $2J_{1}(x)/x=1/{e}$) происходит при $x=2.58383899\dots ,$ а максимум первого кольца приходится на $x=5.13562230\dots .$

Интенсивность $I_{0}$ в центре дифракционной картины относится к полной мощности $P_{0}$ инцидент на проеме

$$I_{0}={\frac {\mathrm {E} _{A}^{2}A^{2}}{2R^{2}}}={\frac {P_{0}A}{\lambda ^{2}R^{2}}}$$

где $\mathrm {E}$ – мощность источника на единицу площади апертуры, А – площадь апертуры ( $A=\pi a^{2}$) и R — расстояние от апертуры. В фокальной плоскости линзы $I_{0}=(P_{0}A)/(\lambda ^{2}f^{2}).$ Интенсивность в максимуме первого кольца составляет около 1,75% от интенсивности в центре диска Эйри.

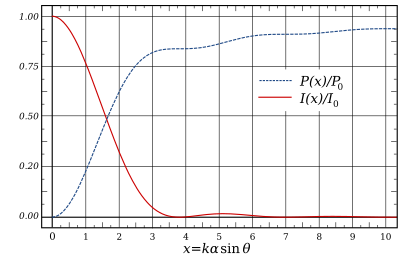
Выражение для $I(\theta )$ приведенное выше, можно проинтегрировать, чтобы получить полную мощность, содержащуюся в дифракционной картине внутри круга заданного размера:

$$P(\theta )=P_{0}[1-J_{0}^{2}(ka\sin \theta )-J_{1}^{2}(ka\sin \theta )]$$

где $J_{0}$ и $J_{1}$ являются функциями Бесселя . Отсюда доли полной мощности, заключенные в первом, втором и третьем темных кольцах (где $J_{1}(ka\sin \theta )=0$) составляют 83,8%, 91,0% и 93,8% соответственно.

Диск Эйри и дифракционная картина могут быть рассчитаны численно на основе первых принципов с использованием интегралов по траекториям Фейнмана.

Паттерн Эйри на интервале ka sin θ = [−10, 10]

Окруженная мощность отображается рядом с интенсивностью.

Аппроксимация с использованием профиля Гаусса

Радиальное сечение модели Эйри (сплошная кривая) и ее аппроксимация гауссова профиля (пунктирная кривая). Абсцисса дана в единицах длины волны. $\lambda$ раз больше f-числа оптической системы.

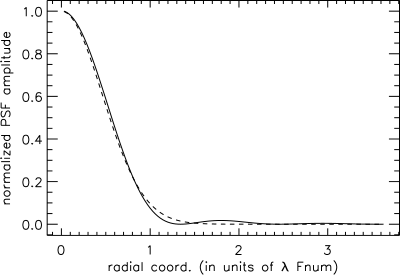
Паттерн Эйри довольно медленно падает до нуля с увеличением расстояния от центра, при этом внешние кольца содержат значительную часть интегрированной интенсивности паттерна. В результате среднеквадратичный размер пятна (RMS) не определен (т.е. бесконечен). Альтернативной мерой размера пятна является игнорирование относительно небольших внешних колец диаграммы Эйри и аппроксимация центрального лепестка гауссовым профилем , так что

$$I(q)\approx I'_{0}\exp \left({\frac {-2q^{2}}{\omega _{0}^{2}}}\right)\ ,$$

где $I'_{0}$ - освещенность в центре рисунка, $q$ представляет радиальное расстояние от центра рисунка, а ${\textstyle \omega _{0}}$ — среднеквадратическая ширина по Гауссу (в одном измерении). Если приравнять пиковую амплитуду диаграммы Эйри и гауссова профиля, то есть $I'_{0}=I_{0},$ и найдите значение ${\textstyle \omega _{0}}$ давая оптимальное приближение к образцу, получаем

${\textstyle \omega _{0}\approx 0.84\lambda N\ ,}$

где N — f-число . Если, с другой стороны, мы хотим обеспечить, чтобы профиль Гаусса имел тот же объем, что и шаблон Эйри, тогда это будет выглядеть следующим образом:

${\textstyle \omega _{0}\approx 0.90\lambda N\ .}$

В теории оптических аберраций принято описывать систему формирования изображения как дифракционно-ограниченную , если радиус диска Эйри больше, чем среднеквадратичный размер пятна, определенный на основе геометрической трассировки лучей (см. Конструкция оптической линзы ). Приближение Гауссова профиля обеспечивает альтернативный способ сравнения: использование приведенного выше приближения показывает, что Гауссова перетяжка ${\textstyle \omega _{0}}$ гауссовского приближения к диску Эйри составляет примерно две трети радиуса диска Эйри, т.е. $0.84\lambda N$ в отличие от $1.22\lambda N.$

Скрытый узор Эйри

Аналогичные уравнения можно вывести и для скрытой дифракционной картины Эйри. которая представляет собой картину дифракции от кольцевого отверстия или луча, т.е. однородного круглого отверстия (луча), закрытого круглым блоком в центре. Эта ситуация актуальна для многих распространенных конструкций телескопов-рефлекторов, включающих вторичное зеркало, включая телескопы Ньютона и телескопы Шмидта-Кассегрена .

$$I(R)={\frac {I_{0}}{(1-\epsilon ^{2})^{2}}}\left({\frac {2J_{1}(x)}{x}}-{\frac {2\epsilon J_{1}(\epsilon x)}{x}}\right)^{2}$$

где $\epsilon$ - коэффициент затемнения кольцевой апертуры, или отношение диаметра затеняющего диска и диаметра апертуры (луча). $\left(0\leq \epsilon <1\right),$ и x определяется, как указано выше: $x=ka\sin(\theta )\approx {\frac {\pi R}{\lambda N}}$ где $R$ — радиальное расстояние в фокальной плоскости от оптической оси, $\lambda$ длина волны и $N$ - f-число системы. Дробная окружённая энергия (доля полной энергии, содержащаяся внутри круга радиуса $R$ с центром на оптической оси в фокальной плоскости) тогда определяется выражением:

$$E(R)={\frac {1}{(1-\epsilon ^{2})}}\left(1-J_{0}^{2}(x)-J_{1}^{2}(x)+\epsilon ^{2}\left[1-J_{0}^{2}(\epsilon x)-J_{1}^{2}(\epsilon x)\right]-4\epsilon \int _{0}^{x}{\frac {J_{1}(t)J_{1}(\epsilon t)}{t}}\,dt\right)$$

Для $\epsilon \rightarrow 0$ формулы сводятся к приведенным выше неясным версиям.

Практический эффект наличия центрального препятствия в телескопе заключается в том, что центральный диск становится немного меньше, а первое яркое кольцо становится ярче за счет центрального диска. Это становится более проблематичным для телескопов с коротким фокусным расстоянием, которым требуются вторичные зеркала большего размера.

Сравнение с фокусом гауссова луча

Круговой лазерный луч с равномерным профилем интенсивности, сфокусированный линзой, образует узор Эйри в фокальной плоскости линзы. Интенсивность в центре фокуса будет $I_{0,Airy}=(P_{0}A)/(\lambda ^{2}f^{2})$ где $P_{0}$ - полная мощность луча, $A=\pi D^{2}/4$ - площадь балки ( $D$ – диаметр пучка), $\lambda$ длина волны, а $f$ — фокусное расстояние линзы.

Гауссовский луч, прошедший через жесткую апертуру, будет ограничен. Энергия теряется, и возникает краевая дифракция, эффективно увеличивающая расходимость. Из-за этих эффектов существует гауссовский диаметр луча, который максимизирует интенсивность в дальней зоне. Это происходит, когда $1/e^{2}$ Диаметр гауссианы составляет 89% от диаметра апертуры, а интенсивность по оси в дальнем поле будет составлять 81% от интенсивности, создаваемой однородным профилем интенсивности.

Эллиптическая апертура

Интеграл Фурье от круглого сечения радиуса $a$ является

$\int _{0}^{a}rdr\int _{0}^{2\pi }d\phi e^{i{\vec {k}}\cdot {\vec {r}}}=\int _{0}^{a}rdr\int _{0}^{2\pi }d\phi e^{ikr\cos \phi }=2\int _{0}^{a}rdr\int _{0}^{\pi }d\phi \cos(kr\cos \phi )=2\pi \int _{0}^{a}rdrJ_{0}(kr)=2\pi {\frac {a}{k}}J_{1}(kr).$

Это частный случай интеграла Фурье эллиптического сечения. с полуосями $a$ и $b$:

$\int _{x^{2}/a^{2}+y^{2}/b^{2}\leq 1}e^{ik_{x}x}e^{ik_{y}y}dxdy=2\pi {\frac {ab}{c}}J_{1}(c)$

где

$c\equiv {\sqrt {(k_{x}a)^{2}+(k_{y}b)^{2}}}.$

См. также

• Любительская астрономия
• Аподизация
• Дифракция Фраунгофера
• Блум (шейдерный эффект)
• Кольца Ньютона
• Оптический блок
• Функция распределения точек
• Кольцо Дебая-Шеррера
• Система Штреля
• Пятнистый узор

Внешние ссылки

• Майкл В. Дэвидсон . «Понятия и формулы в микроскопии: разрешение» . Nikon MicroscopeU (веб-сайт).
  • Кеннет Р. Спринг; Брайан О. Флинн и Майкл В. Дэвидсон. «Формирование изображения: числовая апертура и разрешение изображения» . Проверено 15 июня 2006 г. (Интерактивное руководство по Java) Молекулярные выражения (веб-сайт).
  • Кеннет Р. Спринг; Брайан О. Флинн и Майкл В. Дэвидсон. «Формирование изображения: формирование воздушного узора» . Проверено 15 июня 2006 г. (Интерактивное руководство по Java) Молекулярные выражения .
• Пол Пэдли. «Дифракция на круглой апертуре» . , Connexions (веб-сайт), 8 ноября 2005 г. – Математические детали для вывода приведенной выше формулы.
• «Воздушный диск: объяснение того, что это такое и почему его нельзя избежать» , Oldham Optical UK .
• Вайсштейн, Эрик В. «Нули функции Бесселя» . Математический мир .
• «Расширенный анализ Нийбура-Цернике (ENZ) и поиск аберраций» .