Алгоритм поиска A*

Сорт	Алгоритм поиска
Структура данных	График
Худшая производительность	$O(|E|\log |V|)=O(b^{d})$
Наихудшая пространственная сложность	$O(|V|)=O(b^{d})$

A* (произносится как «А-звезда») — обхода графа и поиска пути алгоритм , который используется во многих областях информатики благодаря своей полноте, оптимальности и оптимальной эффективности. Учитывая взвешенный граф , исходный узел и целевой узел, алгоритм находит кратчайший путь (относительно заданных весов) от источника к цели.

Одним из основных практических недостатков является $O(b^{d})$ пространственная сложность , где d — глубина решения (длина кратчайшего пути), а b — коэффициент ветвления (среднее количество преемников на состояние), поскольку все сгенерированные узлы хранятся в памяти. Таким образом, в практических системах маршрутизации поездок его обычно уступают алгоритмам, которые могут предварительно обрабатывать график для достижения лучшей производительности. а также с помощью подходов, ограниченных памятью; однако A* во многих случаях по-прежнему остается лучшим решением.

Питер Харт , Нильс Нильссон и Бертрам Рафаэль из Стэнфордского исследовательского института (ныне SRI International ) впервые опубликовали алгоритм в 1968 году. Его можно рассматривать как расширение алгоритма Дейкстры . A* достигает большей производительности, используя эвристику для управления поиском.

По сравнению с алгоритмом Дейкстры, алгоритм A* находит только кратчайший путь от указанного источника к указанной цели, а не дерево кратчайшего пути от указанного источника ко всем возможным целям. Это необходимый компромисс для использования эвристики, ориентированной на конкретную цель. Для алгоритма Дейкстры, поскольку генерируется все дерево кратчайшего пути, каждый узел является целью, и не может быть никакой эвристики, направленной на конкретную цель.

История

A* был изобретен исследователями, работавшими над планированием пути робота Шейки.

A* был создан в рамках проекта Shakey , целью которого было создание мобильного робота, способного самостоятельно планировать свои действия. Нильс Нильссон первоначально предложил использовать алгоритм Graph Traverser. для планирования пути Шейки. Graph Traverser руководствуется эвристической функцией h ( n ) — предполагаемым расстоянием от узла n до целевого узла: он полностью игнорирует g ( n ) — расстояние от начального узла до n . Бертрам Рафаэль предложил использовать сумму g ( n ) + h ( n ) . Питер Харт изобрел концепции, которые мы сейчас называем допустимостью и непротиворечивостью эвристических функций. Первоначально A* был разработан для поиска путей с наименьшей стоимостью, когда стоимость пути равна сумме его стоимостей, но было показано, что A* можно использовать для поиска оптимальных путей для любой задачи, удовлетворяющей условиям алгебры стоимости.

Оригинальная бумага A * 1968 года. содержала теорему о том, что ни один A*-подобный алгоритм может расширить меньше узлов, чем A*, если эвристическая функция непротиворечива и правильно выбрано правило разрешения конфликтов для A*. «Поправка» была опубликована несколько лет спустя. утверждая, что последовательность не требуется, но это оказалось ложным в 1985 году в окончательном исследовании Дехтера и Перла оптимальности A* (теперь называемого оптимальной эффективностью), которое дало пример A* с эвристикой, которая была допустимой, но не последовательное расширение произвольно большего количества узлов, чем альтернативный A*-подобный алгоритм.

Описание

Алгоритм поиска пути A*, перемещающийся по случайно сгенерированному лабиринту.

Иллюстрация поиска A* для поиска пути между двумя точками на графике. Слева направо все чаще используется эвристика, отдающая предпочтение точкам, расположенным ближе к цели.

A* — это алгоритм информированного поиска , или поиск по принципу «сначала лучшее» , что означает, что он сформулирован в терминах взвешенных графов : начиная с определенного начального узла графа, он стремится найти путь к заданному целевому узлу, имеющему наименьшее стоимость (наименьшее пройденное расстояние, кратчайшее время и т. д.). Это достигается путем поддержания дерева путей, берущих начало в начальном узле, и расширения этих путей по одному ребру за раз, пока не будет достигнут целевой узел.

На каждой итерации своего основного цикла A* необходимо определить, какой из путей следует расширить. Это делается на основе стоимости пути и оценки стоимости, необходимой для продления пути до цели. В частности, A* выбирает путь, который минимизирует

$f(n)=g(n)+h(n)$

где n — следующий узел на пути, g ( n ) — стоимость пути от начального узла до n , а h ( n ) — эвристическая функция, оценивающая стоимость самого дешевого пути от n до цели. Эвристическая функция зависит от проблемы. Если эвристическая функция допустима (то есть она никогда не переоценивает фактическую стоимость достижения цели), A* гарантированно вернет путь с наименьшими затратами от начала до цели.

Типичные реализации A* используют очередь приоритетов для выполнения повторного выбора узлов с минимальной (оценочной) стоимостью для расширения. Эта приоритетная очередь известна как открытое множество , граница или граница . На каждом шаге алгоритма узел с наименьшим значением f ( x ) удаляется из очереди, значения f и g его соседей соответственно обновляются, и эти соседи добавляются в очередь. Алгоритм продолжается до тех пор, пока удаленный узел (то есть узел с наименьшим значением f из всех краевых узлов) не станет целевым узлом. Значение f этой цели тогда также является стоимостью кратчайшего пути, поскольку h в цели равно нулю в допустимой эвристике.

Описанный до сих пор алгоритм дает нам только длину кратчайшего пути. Чтобы найти фактическую последовательность шагов, алгоритм можно легко пересмотреть, чтобы каждый узел на пути отслеживал своего предшественника. После запуска этого алгоритма конечный узел будет указывать на своего предшественника и так далее, пока предшественник какого-либо узла не станет начальным узлом.

Например, при поиске кратчайшего маршрута на карте h ( x ) может представлять собой расстояние по прямой до цели, поскольку это физически наименьшее возможное расстояние между любыми двумя точками. Для карты-сетки из видеоигры использование расстояния Такси или расстояния Чебышева становится лучше в зависимости от набора доступных движений (4-х или 8-х).

Если эвристика h удовлетворяет дополнительному условию h ( x ) ≤ d ( x , y ) + h ( y ) для каждого ребра ( x , y ) графа (где d обозначает длину этого ребра), то h называется монотонный или последовательный . При последовательной эвристике A* гарантированно найдет оптимальный путь без обработки какого-либо узла более одного раза, а A* эквивалентно запуску алгоритма Дейкстры с уменьшенной стоимостью d' ( x , y ) = d ( x , y )+ h ( y ) - час ( Икс ) .

Псевдокод

Следующий псевдокод описывает алгоритм:

function reconstruct_path(cameFrom, current)    total_path := {current}    while current in cameFrom.Keys:        current := cameFrom[current]        total_path.prepend(current)    return total_path// A* finds a path from start to goal.// h is the heuristic function. h(n) estimates the cost to reach goal from node n.function A_Star(start, goal, h)    // The set of discovered nodes that may need to be (re-)expanded.    // Initially, only the start node is known.    // This is usually implemented as a min-heap or priority queue rather than a hash-set.    openSet := {start}    // For node n, cameFrom[n] is the node immediately preceding it on the cheapest path from the start    // to n currently known.    cameFrom := an empty map    // For node n, gScore[n] is the cost of the cheapest path from start to n currently known.    gScore := map with default value of Infinity    gScore[start] := 0    // For node n, fScore[n] := gScore[n] + h(n). fScore[n] represents our current best guess as to    // how cheap a path could be from start to finish if it goes through n.    fScore := map with default value of Infinity    fScore[start] := h(start)    while openSet is not empty        // This operation can occur in O(Log(N)) time if openSet is a min-heap or a priority queue        current := the node in openSet having the lowest fScore[] value        if current = goal            return reconstruct_path(cameFrom, current)        openSet.Remove(current)        for each neighbor of current            // d(current,neighbor) is the weight of the edge from current to neighbor            // tentative_gScore is the distance from start to the neighbor through current            tentative_gScore := gScore[current] + d(current, neighbor)            if tentative_gScore < gScore[neighbor]                // This path to neighbor is better than any previous one. Record it!                cameFrom[neighbor] := current                gScore[neighbor] := tentative_gScore                fScore[neighbor] := tentative_gScore + h(neighbor)                if neighbor not in openSet                    openSet.add(neighbor)    // Open set is empty but goal was never reached    return failure

Примечание. В этом псевдокоде, если узел достигается одним путем, удаляется из openSet, а затем достигается более дешевым путем, он будет снова добавлен в openSet. Это важно для того, чтобы гарантировать, что возвращаемый путь является оптимальным, если эвристическая функция допустима , но несовместима . Если эвристика непротиворечива, то при удалении узла из openSet путь к нему гарантированно будет оптимальным, поэтому тест ' tentative_gScore < gScore[neighbor]' всегда будет завершаться неудачей, если узел будет достигнут снова.

Иллюстрация поиска A* для поиска пути от начального узла к целевому узлу в робота задаче планирования движения . Пустые кружки представляют собой узлы открытого множества , т. е. те, которые еще предстоит исследовать, а закрашенные — в закрытом множестве. Цвет на каждом закрытом узле указывает на расстояние от цели: чем зеленее, тем ближе. Сначала можно увидеть, как A* движется по прямой в направлении цели, затем при столкновении с препятствием он исследует альтернативные маршруты через узлы из открытого множества.

См. Также: алгоритм Дейкстры.

Пример

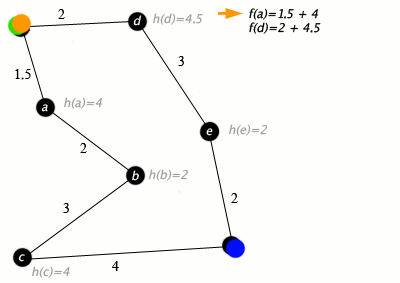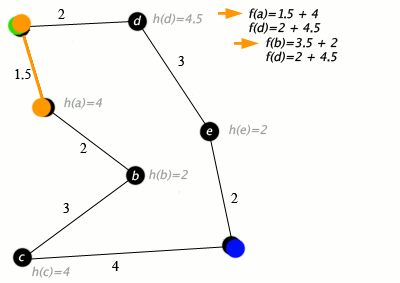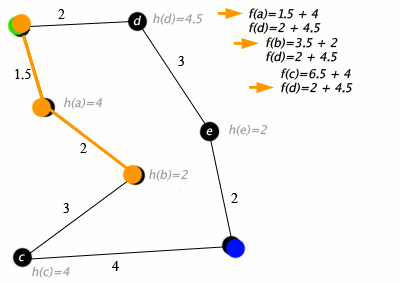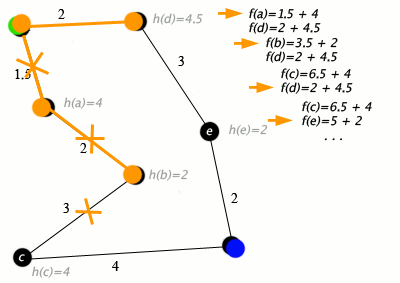
Пример алгоритма A* в действии, где узлами являются города, соединенные дорогами, а h(x) — расстояние по прямой до целевой точки:

Клавиша: зеленая: старт; синий: цель; оранжевый: посетил

Алгоритм A* имеет реальное применение. В этом примере края — это железные дороги, а h(x) — расстояние по большому кругу (кратчайшее возможное расстояние на сфере) до цели. Алгоритм ищет путь между Вашингтоном (округ Колумбия) и Лос-Анджелесом.

Детали реализации

Существует ряд простых оптимизаций или деталей реализации, которые могут существенно повлиять на производительность реализации A*. Первая деталь, на которую следует обратить внимание, заключается в том, что способ обработки связей приоритетной очередью может в некоторых ситуациях существенно влиять на производительность. Если связи нарушены и очередь ведет себя по принципу LIFO , A* будет вести себя как поиск в глубину среди путей с равной стоимостью (избегая исследования более чем одного одинаково оптимального решения).

Когда в конце поиска требуется путь, обычно в каждом узле сохраняется ссылка на родительский узел этого узла. В конце поиска эти ссылки можно использовать для восстановления оптимального пути. Если эти ссылки сохраняются, то может быть важно, чтобы один и тот же узел не появлялся в очереди приоритетов более одного раза (каждая запись соответствует разному пути к узлу и каждая имеет разную стоимость). Стандартный подход здесь — проверить, появился ли уже добавляемый узел в приоритетной очереди. Если да, то указатели приоритета и родительского элемента изменяются, чтобы соответствовать пути с меньшей стоимостью. Стандартная приоритетная очередь на основе двоичной кучи не поддерживает напрямую операцию поиска одного из своих элементов, но ее можно дополнить хеш-таблицей , которая сопоставляет элементы с их положением в куче, позволяя выполнять эту операцию понижения приоритета в логарифмическое время. Альтернативно, куча Фибоначчи может выполнять те же операции с понижением приоритета в константах. амортизированное время .

Особые случаи

Алгоритм Дейкстры , как еще один пример алгоритма поиска с равномерной стоимостью, можно рассматривать как частный случай A*, где ⁠ $h(x)=0$⁠ для всех x . Общий поиск в глубину можно реализовать с использованием A*, если учесть, что существует глобальный счетчик C, инициализированный очень большим значением. Каждый раз, когда мы обрабатываем узел, мы присваиваем C всем его вновь обнаруженным соседям. После каждого присваивания мы уменьшаем счетчик C на единицу. Таким образом, чем раньше обнаружен узел, тем выше его ⁠ $h(x)$⁠ ценность. И алгоритм Дейкстры, и поиск в глубину могут быть реализованы более эффективно без включения ⁠ $h(x)$⁠ значение в каждом узле.

Характеристики

Прекращение и полнота

На конечных графах с неотрицательными весами ребер A* гарантированно завершается и является полным , т. е. всегда найдет решение (путь от начала до цели), если оно существует. На бесконечных графах с конечным фактором ветвления и ценами ребер, отделенными от нуля ( ${\textstyle d(x,y)>\varepsilon >0}$ для некоторых фиксированных $\varepsilon$), A* гарантированно завершится, только если существует решение.

Приемлемость

Алгоритм поиска называется допустимым , если он гарантированно возвращает оптимальное решение. Если эвристическая функция, используемая A*, допустима , то A* допустима. Интуитивное «доказательство» этого состоит в следующем:

Когда A* завершает свой поиск, он нашел путь от начала до цели, фактическая стоимость которого ниже, чем расчетная стоимость любого пути от начала до цели через любой открытый узел ( ⁠ узла $f$⁠ значение). Когда эвристика допустима, эти оценки оптимистичны (не совсем — см. следующий абзац), поэтому A* может безопасно игнорировать эти узлы, поскольку они не могут привести к более дешевому решению, чем то, которое у него уже есть. Другими словами, A* никогда не упустит из виду возможность более дешевого пути от начала до цели и поэтому будет продолжать поиск до тех пор, пока такие возможности не исчезнут.

Настоящее доказательство немного сложнее, потому что ⁠ $f$⁠ значения открытых узлов не гарантированно будут оптимистичными, даже если эвристика допустима. Это потому, что ⁠ $g$⁠ значения открытых узлов не гарантированно будут оптимальными, поэтому сумма ⁠ $g+h$⁠ не обязательно будет оптимистичным.

Оптимальность и последовательность

Алгоритм A оптимально эффективен по отношению к множеству альтернативных алгоритмов Alts на множестве задач P, если для каждой задачи P в P и каждого алгоритма A' в Alts набор узлов, расширенный A при решении P, является подмножеством (возможно, равно) множества узлов, расширенных на A' при решении P. Окончательное исследование оптимальной эффективности A* принадлежит Рине Дехтер и Джуде Перл. Они считали, что различные определения Alts и P в сочетании с эвристикой A* являются просто допустимыми или одновременно непротиворечивыми и допустимыми. Самый интересный положительный результат, который они доказали, заключается в том, что A* с последовательной эвристикой оптимально эффективен по отношению ко всем допустимым A*-подобным алгоритмам поиска для всех «непатологических» задач поиска. Грубо говоря, их представление о непатологической проблеме — это то, что мы сейчас подразумеваем под «вплоть до решения тай-брейка». Этот результат неверен, если эвристика А* допустима, но несовместна. В этом случае Дехтер и Перл показали, что существуют допустимые A*-подобные алгоритмы, которые могут расширять произвольно меньше узлов, чем A*, для некоторых непатологических задач.

Оптимальная эффективность связана с расширенным набором узлов, а не с количеством расширений узлов (количество итераций основного цикла A*). Когда используемая эвристика допустима, но несовместима, узел может быть расширен на A* много раз, в худшем случае – экспоненциальное число раз. В таких обстоятельствах алгоритм Дейкстры может значительно превзойти A*. Однако более поздние исследования показали, что этот патологический случай возникает только в определенных надуманных ситуациях, когда вес ребра графа поиска экспоненциально зависит от размера графа, и что определенные противоречивые (но допустимые) эвристики могут привести к уменьшению количества расширений узлов. в поиске A*.

Ограниченное расслабление

Поиск *, который использует эвристику, которая в 5,0 (=ε) раз превышает непротиворечивую эвристику , и получает неоптимальный путь.

Хотя критерий допустимости гарантирует оптимальный путь решения, он также означает, что A* должен проверить все одинаково эффективные пути, чтобы найти оптимальный путь. Для вычисления приближенных кратчайших путей можно ускорить поиск за счет оптимальности, ослабив критерий допустимости. Часто мы хотим ограничить это расслабление, чтобы гарантировать, что путь решения не хуже, чем (1 + ε ) раз оптимальный путь решения. Эта новая гарантия называется ε -допустимой.

Существует ряд ε -допустимых алгоритмов:

• Взвешенное A*/статическое взвешивание. Если h _a ( n ) является допустимой эвристической функцией, во взвешенной версии поиска A* используется h _w ( n ) = ε h _a ( n ) , ε > 1 в качестве эвристической функции и выполняется поиск A * как обычно (что в конечном итоге происходит быстрее, чем при использовании h _a, поскольку расширяется меньше узлов). Таким образом, путь, найденный алгоритмом поиска, может иметь стоимость, не более чем в ε раз превышающую стоимость пути с наименьшей стоимостью в графе.
• Динамическое взвешивание использует функцию стоимости ⁠ $f(n)=g(n)+(1+\varepsilon w(n))h(n)$⁠ , где $w(n)={\begin{cases}1-{\frac {d(n)}{N}}&d(n)\leq N\\0&{\text{otherwise}}\end{cases}}$, и где ⁠ $d(n)$⁠ — глубина поиска, а N — ожидаемая длина пути решения.
• Выборочное динамическое взвешивание использует выборку узлов для лучшей оценки и устранения эвристической ошибки.
• $A_{\varepsilon }^{*}$. использует две эвристические функции. Первый — это список FOCAL, который используется для выбора узлов-кандидатов, а второй h _F используется для выбора наиболее перспективного узла из списка FOCAL.
• ε _​ выбирает узлы с помощью функции ⁠ $Af(n)+Bh_{F}(n)$⁠ , где A и B — константы. Если ни один узел не может быть выбран, алгоритм вернется с помощью функции ⁠ $Cf(n)+Dh_{F}(n)$⁠ , где C и D — константы.
• Альфа* попытки продвигать эксплуатацию в глубину, отдавая предпочтение недавно расширенным узлам. Alpha* использует функцию стоимости $f_{\alpha }(n)=(1+w_{\alpha }(n))f(n)$, где $w_{\alpha }(n)={\begin{cases}\lambda &g(\pi (n))\leq g({\tilde {n}})\\\Lambda &{\text{otherwise}}\end{cases}}$, где λ и Λ — константы с $\lambda \leq \Lambda$, π ( n ) является родительским узлом n , а ñ является последним расширенным узлом.

Сложность

Временная сложность A* зависит от эвристики. В худшем случае неограниченного пространства поиска количество расширенных узлов экспоненциально зависит от глубины решения (кратчайшего пути) d : O ( b ^д ) , где b — коэффициент ветвления (среднее количество преемников на одно состояние). Это предполагает, что целевое состояние вообще существует и достижимо из начального состояния; если это не так и пространство состояний бесконечно, алгоритм не завершится.

Эвристическая функция оказывает большое влияние на практическую эффективность поиска A*, поскольку хорошая эвристика позволяет A* отсекать многие из b. ^д узлы, которые неосведомленный поиск расширил бы. Его качество можно выразить через эффективный коэффициент ветвления b * , который можно определить эмпирически для конкретного экземпляра задачи путем измерения количества узлов, генерируемых расширением, N и глубины решения, а затем решения

$N+1=1+b^{*}+(b^{*})^{2}+\dots +(b^{*})^{d}.$

Хорошими эвристиками являются эвристики с низким эффективным коэффициентом ветвления (оптимальным является b * = 1 ).

Временная сложность является полиномиальной , когда пространство поиска представляет собой дерево, существует одно целевое состояние и эвристическая функция h удовлетворяет следующему условию:

$|h(x)-h^{*}(x)|=O(\log h^{*}(x))$

где ч ^* — оптимальная эвристика, точная стоимость перехода от x к цели. Другими словами, ошибка h не будет расти быстрее, чем логарифм «совершенной эвристики» h. ^* который возвращает истинное расстояние от x до цели.

Пространственная сложность A* примерно такая же, как и у всех других алгоритмов поиска по графу, поскольку он сохраняет все сгенерированные узлы в памяти. На практике это оказывается самым большим недостатком поиска A*, приводящим к развитию эвристического поиска, ограниченного памятью, такого как итеративное углубление A* , A*, ограниченное памятью, и SMA* .

Приложения

A* часто используется для решения общей задачи поиска пути в таких приложениях, как видеоигры, но изначально был разработан как общий алгоритм обхода графа. Он находит применение в разнообразных задачах, включая задачу синтаксического анализа с использованием стохастических грамматик в НЛП . Другие случаи включают информационный поиск с онлайн-обучением.

Отношения с другими алгоритмами

Что отличает A* от жадного алгоритма поиска по принципу «сначала лучшее», так это то, что он учитывает уже пройденное расстояние g ( n ) .

Некоторые распространенные варианты алгоритма Дейкстры можно рассматривать как частный случай A*, когда эвристика $h(n)=0$ для всех узлов; в свою очередь, и Дейкстра, и А* являются частными случаями динамического программирования . A* само по себе является частным случаем обобщения метода ветвей и границ .

A* аналогичен поиску луча, за исключением того, что при поиске луча сохраняется ограничение на количество путей, которые необходимо исследовать.

Варианты

• В любое время А*
• Блок А*
• Д*
• Поле Д*
• Бахрома
• Дополнительная экономия A* (FSA*)
• Обобщенный адаптивный A* (GAA*)
• Инкрементальный эвристический поиск
• Пониженный А*
• Итеративное углубление A* (IDA*)
• Поиск точки прыжка
• Планирование на всю жизнь A* (LPA*)
• Новый двунаправленный A* (НБА*)
• Упрощенная память, ограниченная A* (SMA*)
• Тета*

A* также можно адаптировать к алгоритму двунаправленного поиска . Особое внимание необходимо уделить критерию остановки.

См. также

• Поиск в ширину
• Поиск в глубину
• Планирование пути под любым углом , поиск путей, которые не ограничиваются движением по краям графа, а могут принимать любой угол.

Дальнейшее чтение

• Нильссон, Нью-Джерси (1980). Принципы искусственного интеллекта . Пало-Альто, Калифорния: Издательская компания Tioga. ISBN  978-0-935382-01-3 .

Внешние ссылки

• Вариант A*, называемый иерархическим поиском пути A* (HPA*).
• Брайан Гринстед. «Алгоритм поиска A* в JavaScript (обновлено)» . Архивировано из оригинала 15 февраля 2020 года . Проверено 8 февраля 2021 г.