Корзина-ручка-арка

Виадук Томаса на железной дороге Балтимора и Огайо как пример арки ручки корзины.

Арка -корзина-ручка представляет собой арку , профиль ее интрадоса (внутренней поверхности) образован последовательностью дуг окружностей, соседние из которых касаются друг друга (плавно переходят), а концевые касаются опор. Например, трехцентровая арка содержит три сегмента дуги с разными центрами; другой распространенный тип — пятицентровый . Арка-корзина-ручка используется в архитектуре, особенно в мостах. Его форма напоминает полуэллипс . который имеет непрерывное изменение кривизны от начала до вершины, т.е. от концов длинной оси до вершины короткой оси. Также известный как вдавленная арка , корзина-арка .

История

Мост Георга V в Орлеане - Трехцентровая арка с ручкой корзины

С римских времен своды мостов строили с полукруглыми арками , образующими полную полуокружность. Начиная с раннего средневековья , сегментная арка , неполная полуокружность, использовалась для строительства сводов, высота которых составляла менее половины высоты их проема.

, Заостренная арка которая вместо того, чтобы уменьшать избыточную высоту сводов, а акцентирует их (поскольку подъем превышает половину проема), не использовалась в мостостроении до средневековья.

Арка-корзина-ручка появилась в начале эпохи Возрождения , предлагая неоспоримое эстетическое преимущество перед сегментным сводом: то, что ее концевые арки расположены вертикально по касательной к опорам.

Мост Рояль в Париже - Трехцентровая арка с ручкой корзины

в Новый мост Тулузе в 16 веке и Королевский мост в следующем столетии. являются самыми ранними приложениями во Франции.

В 18 веке было распространено использование арок с ручками-корзинами, часто с тремя центрами: мосты Визилль , Лавор, Жиньяк , Блуа (1716–1724), Орлеан (1750–1760), Мулен (1756–1764), Сомюр (1756–1770). ).

Жан-Родольф Перроне спроектировал арки мостов Манта (1757–1765), Ножана (1766–1769) и Нейи (1766–1774) с одиннадцатью центрами во второй половине XVIII века. В Туре также было одиннадцать центров (1764–1777). Остальные были сокращены. до 1/3 или немного больше, за исключением Нейи , который был уменьшен до 1/4.

В XIX веке первыми крупными французскими железнодорожными мостами были арочные арки: мост Сен-Марс (1846–1847), мост Пор-де-Пиль (1846–1848), мосты Морандьер: Монлуи (1843–1845), Плесси. -ле-Тур (1855–1857).

В Англии во время Глостерского моста (1826–1827 гг.) и Лондонский мост (1824–1831 гг.) были эллиптическими, мост Ватерлоо в Лондоне (1816–1818) по-прежнему представлял собой арки с ручками-корзинами.

Во второй половине XIX - начале XX века сохранилось несколько арок с ручками-корзинками:

• С тремя центрами: Мост на Эдмонсон-авеню в Балтиморе (1908–1909).
• С пятью центрами: мост Аннибал (1868–1870 гг.). и Чертов мост (1870–1872).
• С семью центрами: Мост Императора Франциска в Праге (1898–1901).
• С девятнадцатью центрами: Мост Синьяк (1871–1872 гг.).

Один арочный железнодорожный мост с корзинчатыми ручками в США, Виадук Томаса , был построен в 1833-1835 годах. Виадук . в настоящее время принадлежит и управляется компанией CSX Transportation и используется до сих пор, что делает его одним из старейших железнодорожных мостов, которые до сих пор находятся в эксплуатации

Сравнение арки ручки корзины и эллипса

Эстетика

Древние архитекторы придавали определенное значение процессам, которые использовались для определения контура арки с ручкой корзины. Легко понять, что эти процессы могут варьироваться до бесконечности , но именно из-за такой гибкости архитекторы часто отдают предпочтение построенной таким образом кривой эллипсу, контур которого определяется геометрически.

В случае эллипса, учитывая проем свода и высоту в центре, т. е. большую и малую оси, все точки интрадосной кривой фиксированы, и архитектор не может ничего изменить по своему желанию. С другой стороны, многоцентровая кривая может быть более или менее закругленной у основания и более или менее сплющенной вверху, в зависимости от расположения центров, оставляя определенное количество на вкус архитектора.

Преимущества и недостатки

Преимущества с точки зрения компоновки были неоспоримы: компоновка полномасштабных канавок считалась более простой и точной, а компоновка нормалей, а значит, и соединений сегментов, осуществлялась сразу на месте.

Число фигур вуссуаров ограничивалось числом различных радиусов, тогда как для эллипса оно равнялось половине числа вуссуаров плюс один.

Однако прерывистость планировки привела к появлению неприглядных вуссуаров, которые не всегда можно было убрать при реставрационных работах.

Трассировка кривых с тремя центрами

Древний овал

Трассировка трехцентровой бухты по методу Герона Александрийского (без строительных кругов)

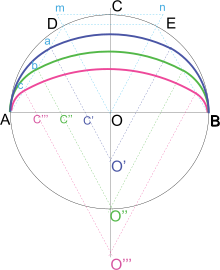
не использовалась для мостовых сводов Хотя арка-корзина-ручка в древности , иногда ее использовали при строительстве других сводов. А Герон Александрийский (написавший свои математические трактаты более чем за столетие до нашей эры) уже определил простой метод его отслеживания.

Если АВ — ширина строящегося свода, а его высота (или подъем, или шпиль) неопределенна, то описываем на АВ полуокружность и через точку С ее, взятую на вертикали ОС, проводим касательная mn, на которой примем длины Cm и Cn равными половине радиуса. Соединив mO и nO, мы определим точки D и E, через которые проведем равнобедренный треугольник DOE, основание которого равно высоте. Как только это будет сделано, берем линию DA, делим ее на четыре равные части и проводим параллели ДО через точки деления a, b, c. Точки, в которых эти параллели пересекают горизонтальную ось AB и расширенную вертикальную ось CO, дают центры, которые нам нужны для прослеживания различных кривых с 3 центрами на AB, как показано на рисунке. Эти кривые и есть то, что мы обычно называем древним овалом.

Трассировка трехцентровой бухты по методу Герона Александрийского (с строительными кругами)

Поскольку арка-корзина-ручка получила широкое распространение в мостостроении, способы ее прослеживания умножились, а число центров увеличилось. Ниже приводится краткое описание наиболее широко используемых из этих процедур.

Целью было создать идеально непрерывные кривые с элегантным контуром. Ввиду неопределенности характера задачи были произвольно наложены определенные условия, исходя из предположения, что они с большей надежностью приведут к желаемому результату.

Иногда, например, считалось, что различные дуги окружности, из которых состоит кривая, должны соответствовать равным углам в центре; иногда предполагалось, что эти частичные дуги имеют одинаковую длину, или же разрешалось изменять либо амплитуду углов, либо длину последовательных лучей в определенных пропорциях.

Кроме того, всегда считалось, что между опусканием арки и числом центров, используемых для прослеживания кривой интрадоса, должно поддерживаться определенное соотношение, таким образом измеряется понижение как для арки с ручкой корзины, так и для дуги окружности , по отношением подъема к проему, т.е. соотношением b/2a, где b – подъем, а 2a – ширина арки.

Это соотношение может составлять одну треть, одну четверть, одну пятую или меньше, но как только оно падает ниже одной пятой, дугу окружности обычно следует отдавать предпочтение арке с ручкой корзины или эллипсу. При большем уклоне рекомендуется иметь как минимум пять центров, а иногда мы допускаем до одиннадцати, как в случае с поворотом моста Нейи , или даже до девятнадцати для моста Синьяк. Поскольку один из центров всегда должен находиться на вертикальной оси, а остальные симметрично располагаться в равном количестве справа и слева, общее число всегда нечетное.

Метод Гюйгенса

След трехцентровой бухты методом Гюйгенса.

Для кривых с тремя центрами следующая процедура, по Гюйгенсу, состоит в том, чтобы проследить их, приведя дуги разных радиусов в соответствие равным углам, т. е. углам 60°.

Учитывая АВ как проем и ОЕ как стрелку свода, из центра О, с ОА как радиус, опишем дугу АМФ, от которой возьмем дугу АМ, равную одной шестой окружности, хорда которой следовательно, равен радиусу ОА. Нарисуйте эту хорду AM и хорду MF, затем проведите Em через точку Е, конец малой оси, параллельно MF.

Пересечение AM и Em определяет границу m первой дуги. Проведя линию mP параллельно MO через эту точку m, точки n и P станут двумя искомыми центрами. Третий центр n расположен на расстоянии n'O от оси ОЕ, равном nO. Достаточно изучить рисунок, чтобы увидеть, что три дуги окружности Am, mEm', m'B, составляющие кривую, соответствуют углам при центрах Anm, mPm' и m'n'B, равным каждой остальные и все три по 60°.

Метод Боссута

Трассировка трехцентровой бухты по методу Боссю.

Следующий метод Шарля Боссю для отслеживания той же трехцентровой кривой работает быстрее.

АВ и ОЕ — это снова отверстие и стрелка свода, т. е. длинная и короткая оси прослеживаемой кривой. Соединяем АЕ и из точки Е принимаем EF' равным ОА-ОЕ, затем проводим перпендикуляр через середину m AF' и точки n и P, где этот перпендикуляр пересекает большую ось и продолжение малая ось — это те два центра, которые мы ищем.

При одинаковом раскрытии и подъеме нарисованная таким образом кривая мало чем отличается от предыдущей.

Кривые с более чем тремя центрами

Для кривых с более чем тремя центрами методы, указанные Бераром, Жаном-Родольфом Перроне , Эмиландом Готи и другими, заключались, как и для моста Нейи , в действиях методом проб и ошибок.

Вычерчивание первой приближенной кривой по произвольным данным, элементы которой затем уточнялись по более или менее определенным формулам так, чтобы они проходили точно через окончания большой и малой осей.

Метод Михала

Трассировка семицентровой бухты методом Михала.

В статье, опубликованной в 1831 году, г-н Михал подошел к вопросу более научно и подготовил таблицы, содержащие данные, необходимые для построения кривых с 5, 7 и 9 центрами без проб и ошибок и с идеальной точностью.

Его метод расчета можно применить и к кривым с любым количеством центров.

Поскольку условия, которые должны быть выполнены для того, чтобы проблема перестала быть неопределенной, отчасти произвольны, г-н Михал предлагает, чтобы кривые состояли иногда из дуг окружности, образующих равные углы, иногда из дуг равной длины. Поскольку этого недостаточно для определения всех радиусов, он предполагает также, что радиусы каждой дуги равны радиусам кривизны эллипса, описанного в центре этих дуг, с отверстием в качестве большой оси и восхождением в качестве главной оси. малая ось.

По мере увеличения числа центров кривая становится все ближе и ближе к эллипсу с тем же раскрытием и наклоном.

Следующая таблица относится к чертежу арки корзины-ручки с равенством углов, образуемых частями дуг, из которых она состоит. Пропорциональные значения, которые он дает для первых радиусов, рассчитываются с использованием полуоткрытия в качестве единицы измерения. Свес – это отношение стрелки ко всему проему.

5 центров		7 центров			9 центров
Уронить	1-й радиус	Уронить	1-й радиус	2-й радиус	Уронить	1-й радиус	2-й радиус	3-й радиус
0,36	0,556	0,33	0,455	0,63	0,25	0,259	0,341	0,597
0,35	0,53	0,32	0,431	0,604	0,24	0,24	0,318	0,556
0,34	0,504	0,31	0,406	0,578	0,23	0,222	0,296	0,535
0,33	0,477	0,3	0,383	0,551	0,22	0,203	0,276	0,504
0,32	0,45	0,29	0,359	0,525	0,21	0,185	0,251	0,474
0,31	0,423	0,28	0,346	0,498	0,2	0,166	0,228	0,443
0,3	0,396	0,27	0,312	0,472
		0,26	0,289	0,445
		0,25	0,265	0,419

Легко понять, как можно использовать эту таблицу, чтобы нарисовать арку с ручкой корзины с любым отверстием в пяти, семи или девяти центрах, не проводя никаких исследований. Единственное требование – чтобы падение было именно таким, как предсказывает г-н Михал.

Например, нам нужно нарисовать кривую с семью центрами, проемом 12 метров и уклоном 3 метра, соответствующим четверти или двадцати пятисотой доли. Первый и второй радиусы составляют 6 х 0,265 и 6 х 0,419 или 1,594 и 2,514.

Если ABCD — прямоугольник, в который надо вписать кривую , то полуокружность на AB описываем как диаметр , разделив его на семь равных частей и проведя хорды Aa, ab, bc, cd, причем последняя соответствует половине -разделение.

На оси АВ, начиная с точки А, возьмем длину, равную 1,590 м, и имеем первый центр m1. Через эту точку проведена параллель радиуса Оа, а точка n, где она пересекает хорду Аа, является пределом первой дуги. От точки n возьмем длину nm2, равную 2,514 м, а точку m2 — второй центр. Из этой точки m2 проводим параллель радиусу Ob , из точки na параллельно хорде ab, а точка пересечения n' этих двух параллелей является пределом второй дуги. Затем через точку n' проведем параллель хорде bc, а через точку Е — параллель хорде cd.

Наконец, в точке пересечения n'' этих двух прямых проводится параллель радиуса Ос, а точки m3, m4, где она пересекает протяженность радиуса n'm2 и протяженность вертикальной оси, дают третий и четвертый центры. Последние три центра m5, m6 и m7 симметричны относительно первых трех m1, m2 и m3.

Как видно из рисунка, дуги An, nn', n'n'' и т. д. соответствуют равным центральным углам и da 51° 34' 17" 14. Более того, если бы мы построили полуэллипс с AB и О.Е. как большая и малая оси, дуги этого полуэллипса, заключенные в тех же углах, что и дуги окружности, имели бы в своем центре радиус кривизны, равный радиусу последней.

Этот метод позволяет с одинаковой легкостью строить кривые с пятью, семью и девятью центрами.

Метод Леружа

После г-на Михаля этой темой снова занялся г-н Леруж, главный инженер Ponts et Chaussées , который также составил таблицы для прослеживания кривых с тремя, пятью, семью и до пятнадцати центров.

Однако его расчеты основаны на том условии, что последовательные радиусы увеличиваются в арифметической прогрессии, независимо от равенства углов, которые они образуют между собой.

Ссылки

Библиография

• «Примечание о кривых ручках корзин, используемых при строительстве мостов». Летопись мостов и дорог. Мемуары и документы, касающиеся строительного искусства и службы инженера (на французском языке). Зороастр Алексис Михал. Париж: Карильян-Гёри. 1831. 49-61. {{cite book}}: CS1 maint: другие ( ссылка )
• «Память на сводах ручек корзин». Летопись мостов и дорог. Мемуары и документы, касающиеся строительного искусства и службы инженера (на французском языке). Пьер-Жак Леруж. Париж: Карильян-Гёри. 1839.стр. 335–362. {{cite book}}: CS1 maint: другие ( ссылка )
• Дегранд, Юджин; Ресаль, Жан (1887). Мосты и каменная кладка (на французском языке). Полет. 2. Париж: Бодри.
• Сежурне, Поль (1913). Великие своды: Часть 1 - нечленораздельные своды (на французском языке). Полет. 1. Бурж: Imprimerie Vve Tardy-Pigelet et fils.
• Сежурне, Поль (1913). Великие своды: невнятные своды (продолжение) (на французском языке). Полет. 3. Бурж: Imprimerie Vve Tardy-Pigelet et fils.
• Министерство транспорта, Управление автомобильных дорог (1982 год). Каменные мосты (PDF) (PDF) (на французском языке). Банье.
• Прад, Марсель (1986). Мосты, исторические памятники: инвентарь, описание, история мостов и акведуков во Франции, охраняемых как исторические памятники (на французском языке). Брисо. ISBN  978-2902170548 .
• Прад, Марсель (1988). Мосты и виадуки в девятнадцатом веке (на французском языке). Брисо. ISBN  978-2902170593 .
• Прад, Марсель (1990). Великие мосты мира. Замечательные мосты Европы (на французском языке). Брисо. ISBN  9782902170654 .
• Вудман, Фрэнсис; Блум, Джонатан М. (2003). «Арка». Оксфордское искусство онлайн . Издательство Оксфордского университета. дои : 10.1093/gao/9781884446054.article.t003657 . ISBN  978-1-884446-05-4 .
• Американское техническое общество (1920). «Арка-корзина-ручка» . Циклопедия гражданского строительства . Проверено 5 апреля 2024 г.
• Бейкер, ИО (1889 г.). «Арка-корзина-ручка» . Трактат о каменном строительстве . Дж. Уайли и сыновья . Проверено 5 апреля 2024 г.