Бесконечная импульсная характеристика

Бесконечная импульсная характеристика ( БИХ ) — это свойство, применимое ко многим линейным, инвариантным ко времени системам , которые отличаются наличием импульсной характеристики. $h(t)$ после определенной точки оно не становится точно нулевым, а продолжается бесконечно. Это контрастирует с системой с конечной импульсной характеристикой (FIR), в которой импульсная характеристика . иногда становится точно равной нулю $t>T$ для некоторого конечного $T$, таким образом, имеет конечную продолжительность. Типичными примерами линейных стационарных систем являются большинство электронных и цифровых фильтров . Системы с этим свойством известны как БИХ-системы или БИХ-фильтры .

На практике импульсная характеристика даже БИХ-систем обычно приближается к нулю, и после определенного момента ею можно пренебречь. Однако физические системы, вызывающие реакции IIR или FIR, различны, и в этом заключается важность различия. Например, аналоговые электронные фильтры, состоящие из резисторов, конденсаторов и/или катушек индуктивности (и, возможно, линейных усилителей), обычно являются БИХ-фильтрами. С другой стороны, фильтры с дискретным временем (обычно цифровые фильтры), основанные на отводной линии задержки и не использующие обратную связь, обязательно являются КИХ-фильтрами. Конденсаторы (или катушки индуктивности) в аналоговом фильтре имеют «память», и их внутреннее состояние никогда полностью не расслабляется после импульса (при условии, что используется классическая модель конденсаторов и катушек индуктивности, в которой квантовые эффекты игнорируются). Но в последнем случае, после того как импульс достиг конца отводной линии задержки, система больше не запоминает этот импульс и возвращается в исходное состояние; его импульсный отклик за пределами этой точки равен нулю.

Реализация и дизайн

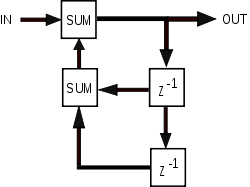
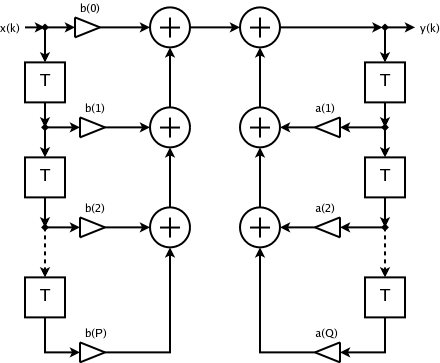
Хотя почти все аналоговые электронные фильтры являются БИХ, цифровые фильтры могут быть как БИХ, так и КИХ. Наличие обратной связи в топологии фильтра дискретного времени (например, блок-схемы, показанной ниже) обычно создает БИХ-отклик. Передаточная области z функция БИХ-фильтра содержит нетривиальный знаменатель, описывающий эти члены обратной связи. С другой стороны, передаточная функция КИХ-фильтра имеет только числитель, выраженный в общей форме, полученной ниже. Все $a_{i}$ коэффициенты с $i>0$ (члены обратной связи) равны нулю, и фильтр не имеет конечных полюсов .

Передаточные функции, относящиеся к аналоговым электронным фильтрам БИХ, были тщательно изучены и оптимизированы по их амплитудным и фазовым характеристикам. Эти функции фильтра непрерывного времени описаны в области Лапласа . Желаемые решения могут быть перенесены на случай фильтров с дискретным временем, передаточные функции которых выражены в области z, посредством использования определенных математических методов, таких как билинейное преобразование , импульсная инвариантность или метод согласования полюса и нуля . Таким образом, цифровые БИХ-фильтры могут быть основаны на хорошо известных решениях для аналоговых фильтров, таких как фильтр Чебышева , фильтр Баттерворта и эллиптический фильтр , наследуя характеристики этих решений.

Вывод передаточной функции

Цифровые фильтры часто описываются и реализуются с помощью разностного уравнения , которое определяет, как выходной сигнал связан с входным сигналом:

${\begin{aligned}y[n]{}=&{\frac {1}{a_{0}}}(b_{0}x[n]+b_{1}x[n-1]+\cdots +b_{P}x[n-P]\\&{}-a_{1}y[n-1]-a_{2}y[n-2]-\cdots -a_{Q}y[n-Q])\end{aligned}}$

где:

• $\ P$ порядок фильтра прямой связи
• $\ b_{i}$ коэффициенты фильтра прямой связи
• $\ Q$ это порядок фильтра обратной связи
• $\ a_{i}$ коэффициенты фильтра обратной связи
• $\ x[n]$ это входной сигнал
• $\ y[n]$ является выходным сигналом.

Более сжатая форма разностного уравнения:

$\ y[n]={\frac {1}{a_{0}}}\left(\sum _{i=0}^{P}b_{i}x[n-i]-\sum _{j=1}^{Q}a_{j}y[n-j]\right)$

который при перестановке становится:

$\ \sum _{j=0}^{Q}a_{j}y[n-j]=\sum _{i=0}^{P}b_{i}x[n-i]$

Чтобы найти передаточную функцию фильтра, мы сначала возьмем Z-преобразование каждой части приведенного выше уравнения, где мы используем свойство временного сдвига , чтобы получить:

$\ \sum _{j=0}^{Q}a_{j}z^{-j}Y(z)=\sum _{i=0}^{P}b_{i}z^{-i}X(z)$

Мы определяем передаточную функцию как:

${\begin{aligned}H(z)&={\frac {Y(z)}{X(z)}}\\&={\frac {\sum _{i=0}^{P}b_{i}z^{-i}}{\sum _{j=0}^{Q}a_{j}z^{-j}}}\end{aligned}}$

Учитывая, что в большинстве конструкций БИХ-фильтров коэффициент $\ a_{0}$ равно 1, передаточная функция БИХ-фильтра принимает более традиционную форму:

$H(z)={\frac {\sum _{i=0}^{P}b_{i}z^{-i}}{1+\sum _{j=1}^{Q}a_{j}z^{-j}}}$

Пример структурной схемы БИХ-фильтра. $z^{-1}$ блок — это единичная задержка.

Стабильность

Передаточная функция позволяет судить, является ли система стабильной с ограниченным входом и ограниченным выходом (BIBO) . Точнее, критерий устойчивости BIBO требует, чтобы ROC системы включал единичный круг. Например, для причинной системы все полюса передаточной функции должны иметь абсолютное значение меньше единицы. Другими словами, все полюса должны быть расположены внутри единичного круга в $z$-самолет.

Полюсы определяются как значения $z$ которые составляют знаменатель $H(z)$ равно 0:

$\ 0=\sum _{j=0}^{Q}a_{j}z^{-j}$

Ясно, что если $a_{j}\neq 0$ тогда полюса не расположены в начале координат $z$-самолет. В этом отличие от КИХ- фильтра, где все полюса расположены в начале координат и поэтому всегда стабильны.

БИХ-фильтры иногда предпочтительнее КИХ-фильтров, поскольку БИХ-фильтр может обеспечить гораздо более резкий спад в переходной области , чем КИХ-фильтр того же порядка.

Пример

Пусть передаточная функция $H(z)$ фильтра дискретного времени будет иметь вид:

$H(z)={\frac {B(z)}{A(z)}}={\frac {1}{1-az^{-1}}}$

регулируется параметром $a$, действительное число с $0<|a|<1$. $H(z)$ стабильна и причинна с полюсом в $a$. во временной области импульсная характеристика Можно показать, что определяется следующим образом:

$h(n)=a^{n}u(n)$

где $u(n)$ — единичная ступенчатая функция . Видно, что $h(n)$ ненулевое значение для всех $n\geq 0$, таким образом, импульсный отклик, который продолжается бесконечно.

Пример БИХ-фильтра

Преимущества и недостатки

Основное преимущество цифровых БИХ-фильтров перед КИХ-фильтрами заключается в их эффективности в реализации, позволяющей соответствовать спецификациям с точки зрения полосы пропускания, полосы задерживания, пульсаций и/или спада. Такой набор характеристик может быть достигнут с помощью БИХ-фильтра более низкого порядка ( Q в приведенных выше формулах), чем требуется для КИХ-фильтра, отвечающего тем же требованиям. Если это реализовано в процессоре сигналов, это подразумевает соответственно меньшее количество вычислений за временной шаг; экономия вычислительных ресурсов часто имеет довольно большое значение.

С другой стороны, КИХ-фильтры проще спроектировать, например, чтобы они соответствовали определенным требованиям к частотной характеристике. Это особенно верно, когда требование не является одним из обычных случаев (высокочастотный, низкочастотный, режекторный и т. д.), которые были изучены и оптимизированы для аналоговых фильтров. Кроме того, КИХ-фильтры можно легко сделать линейными по фазе (постоянная групповая задержка в зависимости от частоты) — свойство, которое нелегко реализовать при использовании БИХ-фильтров, и то только в качестве приближения (например, с фильтром Бесселя ). Еще одна проблема, связанная с цифровыми БИХ-фильтрами, — это возможность поведения предельного цикла в режиме ожидания из-за системы обратной связи в сочетании с квантованием.

Методы проектирования

Импульсная инвариантность

Импульсная инвариантность - это метод разработки фильтров с бесконечной импульсной характеристикой (БИХ) дискретного времени на основе фильтров с непрерывным временем, в котором импульсная характеристика системы с непрерывным временем дискретизируется для получения импульсной характеристики системы с дискретным временем. Импульсная инвариантность — один из часто используемых методов для удовлетворения двух основных требований отображения из s-плоскости в z-плоскость. Это получается путем решения T(z), который имеет то же выходное значение в то же время выборки, что и аналоговый фильтр, и применим только тогда, когда входные сигналы являются импульсными.
Обратите внимание, что все входные данные цифрового фильтра, генерируемые этим методом, являются приблизительными значениями, за исключением очень точных импульсных входов. Это самый простой метод создания БИХ-фильтра. Он наиболее точен на низких частотах, поэтому обычно используется в фильтрах нижних частот.

Для преобразования Лапласа или z-преобразования выходные данные после преобразования — это просто входные данные, умноженные на соответствующую функцию преобразования T(s) или T(z). Y(s) и Y(z) — это преобразованные выходные данные входа X(s) и входа X(z) соответственно.

$Y(s)=T(s)X(s)$

$Y(z)=T(z)X(z)$

При применении преобразования Лапласа или z-преобразования к единичному импульсу результат равен 1. Следовательно, выходные результаты после преобразования равны

$Y(s)=T(s)$

$Y(z)=T(z)$

Теперь выходной сигнал аналогового фильтра — это просто обратное преобразование Лапласа во временной области.

$y(t)=L^{-1}[Y(s)]=L^{-1}[T(s)]$

Если мы используем nT вместо t, мы можем получить выходной сигнал y(nT), полученный из импульса во время выборки. Это также можно выразить как y(n)

$y(n)=y(nT)=y(t)|_{t=sT}$

К этому сигналу дискретного времени можно применить z-преобразование, чтобы получить T(z)

$T(z)=Y(z)=Z[y(n)]$

$T(z)=Z[y(n)]=Z[y(nT)]$

$T(z)=Z\left\{L^{-1}[T(s)]_{t=nT}\right\}$

Последнее уравнение математически описывает, что цифровой БИХ-фильтр должен выполнять z-преобразование аналогового сигнала, который был дискретизирован и преобразован в T(s) Лапласом, что обычно упрощается до

$T(z)=Z[T(s)]*T$

Обратите внимание на то, что в формуле присутствует множитель Т. Это связано с тем, что даже если преобразование Лапласа и z-преобразование для единичного импульса равны 1, сам импульс не обязательно один и тот же. Для аналоговых сигналов импульс имеет бесконечное значение, но площадь равна 1 при t=0, но равна 1 при импульсе с дискретным временем t=0, поэтому требуется наличие множителя T.

Шаговая инвариантность

Ступенчатая инвариантность — лучший метод проектирования, чем импульсный инвариант. Цифровой фильтр имеет несколько входных сегментов с разными константами при дискретизации, состоящей из дискретных шагов. Ступенчато-инвариантный БИХ-фильтр менее точен, чем тот же входной ступенчатый сигнал для АЦП. Однако это лучшее приближение для любого входа, чем импульсный инвариант.
Шаговый инвариант решает проблему одних и тех же выборочных значений, когда T(z) и T(s) являются входными данными шага. Вход цифрового фильтра — u(n), а вход аналогового фильтра — u(t). Примените z-преобразование и преобразование Лапласа к этим двум входным параметрам, чтобы получить преобразованный выходной сигнал.
Выполнить z-преобразование при пошаговом вводе $Z[u(n)]={\dfrac {z}{z-1}}$
Преобразованный результат после z-преобразования $Y(z)=T(z)U(z)=T(z){\dfrac {z}{z-1}}$
Выполните преобразование Лапласа при пошаговом вводе $L[u(t)]={\dfrac {1}{s}}$
Преобразованный результат после преобразования Лапласа $Y(s)=T(s)U(s)={\dfrac {T(s)}{s}}$
Выходной сигнал аналогового фильтра — y(t), который является обратным преобразованием Лапласа Y(s). Если выборка выполняется каждые T секунд, это y(n), что является обратным преобразованием Y(z). Эти сигналы используются для расчета цифрового фильтра и аналогового фильтра и имеют одинаковый выходной сигнал во время выборки.
Следующее уравнение указывает на решение T(z), которое является приближенной формулой для аналогового фильтра.

$T(z)={\dfrac {z-1}{z}}Y(z)$

$T(z)={\dfrac {z-1}{z}}Z[y(n)]$

$T(z)={\dfrac {z-1}{z}}Z[Y(s)]$

$T(z)={\dfrac {z-1}{z}}Z[{\dfrac {T(s)}{s}}]$

Билинейное преобразование

Билинейное преобразование — это частный случай конформного отображения, часто используемого для преобразования передаточной функции. $H_{a}(s)$ линейного, нестационарного (LTI) фильтра в области непрерывного времени (часто называемого аналоговым фильтром) к передаточной функции $H_{d}(z)$ линейного, инвариантного к сдвигу фильтра в области дискретного времени. Билинейное преобразование представляет собой аппроксимацию первого порядка функции натурального логарифма, которая является точным отображением плоскости z в плоскость s . Когда преобразование Лапласа выполняется над сигналом дискретного времени (когда каждый элемент последовательности дискретного времени прикреплен к соответственно задержанному единичному импульсу), результатом является в точности Z-преобразование последовательности дискретного времени с заменой

${\begin{aligned}z&=e^{sT}\\&={\frac {e^{sT/2}}{e^{-sT/2}}}\\&\approx {\frac {1+sT/2}{1-sT/2}}\end{aligned}}$

где $T$ – размер шага численного интегрирования правила трапеций, используемого при выводе билинейного преобразования; или, другими словами, период выборки. Вышеупомянутое билинейное приближение можно решить для $s$ или аналогичное приближение для $s=(1/T)\ln(z)$ можно выполнить.

Обратное к этому отображению (и его билинейное приближение первого порядка) равно

${\begin{aligned}s&={\frac {1}{T}}\ln(z)\\&={\frac {2}{T}}\left[{\frac {z-1}{z+1}}+{\frac {1}{3}}\left({\frac {z-1}{z+1}}\right)^{3}+{\frac {1}{5}}\left({\frac {z-1}{z+1}}\right)^{5}+{\frac {1}{7}}\left({\frac {z-1}{z+1}}\right)^{7}+\cdots \right]\\&\approx {\frac {2}{T}}{\frac {z-1}{z+1}}\\&={\frac {2}{T}}{\frac {1-z^{-1}}{1+z^{-1}}}\end{aligned}}$

Это соотношение используется в передаточной функции Лапласа любого аналогового фильтра или в цифровом фильтре с бесконечной импульсной характеристикой (БИХ) T(z) аналогового фильтра.
Билинейное преобразование по существу использует это приближение первого порядка и заменяет его передаточной функцией с непрерывным временем: $H_{a}(s)$

$s\leftarrow {\frac {2}{T}}{\frac {z-1}{z+1}}.$

То есть

$H_{d}(z)=H_{a}(s){\bigg |}_{s={\frac {2}{T}}{\frac {z-1}{z+1}}}=H_{a}\left({\frac {2}{T}}{\frac {z-1}{z+1}}\right).\$

который используется для расчета цифрового БИХ-фильтра, исходя из передаточной функции Лапласа аналогового фильтра.

См. также

• Авторегрессионная модель
• Электронный фильтр
• Конечная импульсная характеристика
• Рекуррентное соотношение , математическая формализация
• Системный анализ

Внешние ссылки

• Пятый модуль курса BORES Signal Processing DSP — Введение в DSP ] ​​на Wayback Machine (архив от 2 июля 2016 г.)
• Апплет проектирования цифрового фильтра IIR на Wayback Machine (архивировано 13 февраля 2010 г.)
• Инструмент проектирования цифрового IIR-фильтра — создает коэффициенты, графики, полюса, нули и код C.
• EngineerJS Online IIR Design Tool — не требует Java