Эйлеров кирпич

В математике кирпич Эйлера , названный в честь Леонарда Эйлера , представляет собой прямоугольный кубоид которого , ребра и диагонали грани имеют целые длины. Примитивный кирпич Эйлера — это кирпич Эйлера, длины ребер которого относительно просты . Совершенный кирпич Эйлера которого — это такой кирпич, пространственная диагональ также является целым числом, но такой кирпич ещё не найден.

Определение

Определение кирпичика Эйлера в геометрическом плане эквивалентно решению следующей системы диофантовых уравнений :

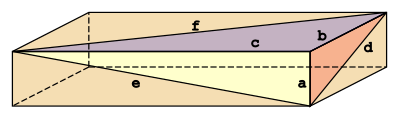
{\begin{cases}a^{2}+b^{2}=d^{2}\\a^{2}+c^{2}=e^{2}\\b^{2}+c^{2}=f^{2}\end{cases}}

где $a, b, c$ — ребра, а $d, e, f$ — диагонали.

Характеристики

Если $(a, b, c)$ является решением, то $(ka, kb, kc)$ также является решением для любого $k$ . Следовательно, все решения в рациональных числах являются масштабированием целочисленных решений. Учитывая кирпич Эйлера с длинами ребер $(a, b, c)$ , тройка $(bc, ac, ab)$ также представляет собой кирпич Эйлера. ^[1]^{: с. 106}

Ровно одно ребро и две грани примитивного кирпича Эйлера нечетны.

По крайней мере два ребра кирпича Эйлера делятся на 3. ^[1]^{: с. 106}

По крайней мере два ребра кирпича Эйлера делятся на 4. ^[1]^{: с. 106}

Хотя бы одно ребро кирпича Эйлера делится на 11. ^[1]^{: с. 106}

Примеры

Самый маленький кирпичик Эйлера, открытый Паулем Хальке в 1719 году, имеет ребра $(a, b, c) = (44, 117, 240)$ и диагонали грани $(d, e, f) = (125, 244, 267)$ . ^[2] Некоторые другие небольшие примитивные решения, представленные как ребра $(a, b, c)$ — диагонали грани $(d, e, f)$ , приведены ниже:

(	85,	132,	720	) — (	157,	725,	732	)
(	140,	480,	693	) — (	500,	707,	843	)
(	160,	231,	792	) — (	281,	808,	825	)
(	187,	1020,	1584	) — (	1037,	1595,	1884	)
(	195,	748,	6336	) — (	773,	6339,	6380	)
(	240,	252,	275	) — (	348,	365,	373	)
(	429,	880,	2340	) — (	979,	2379,	2500	)
(	495,	4888,	8160	) — (	4913,	8175,	9512	)
(	528,	5796,	6325	) — (	5820,	6347,	8579	)

Генерирующая формула

Эйлер нашел по крайней мере два параметрических решения проблемы, но ни одно из них не дает всех решений. ^[3]

Бесконечное количество кирпичиков Эйлера можно сгенерировать с помощью Сондерсона . формулы ^[4] параметрическая формула . Пусть $(u, v, w)$ — тройка Пифагора (т. е. $u 2 + v 2 = v 2$ .) Затем ^[1]^: 105 края

a=u|4v^{2}-w^{2}|,\quad b=v|4u^{2}-w^{2}|,\quad c=4uvw

придать лицу диагонали

d=w^{3},\quad e=u(4v^{2}+w^{2}),\quad f=v(4u^{2}+w^{2}).

Существует множество кирпичей Эйлера, которые не параметризованы, как указано выше, например кирпич Эйлера с ребрами $(a, b, c) = (240, 252, 275)$ и диагоналями граней $(d, e, f) = (348, 365, 373)$ .

Идеальный кубоид

Нерешенная задача по математике :

Существует ли идеальный кубоид?

(еще нерешенные задачи по математике)

Совершенный кубоид (также называемый идеальным кирпичом Эйлера или идеальным ящиком ) — это кирпич Эйлера, пространственная диагональ которого также имеет целую длину. Другими словами, к системе диофантовых уравнений, определяющей кирпичик Эйлера, добавляется следующее уравнение:

a^{2}+b^{2}+c^{2}=g^{2},

где $g$ — диагональ пространства. По состоянию на май 2023 г. ^[update], ни одного примера идеального кубоида не было найдено, и никто не доказал, что таковой существует. ^[5]

Тщательные компьютерные исследования показывают, что если существует идеальный кубоид,

нечетное ребро должно быть больше 2,5 × 10 ¹³, ^[5]
наименьшее ребро должно быть больше 5 × 10 ¹¹. ^[5]
диагональ пространства должна быть больше 9 × 10 ¹⁵. ^[6]

известны некоторые факты о свойствах, которым должен удовлетворять примитивный На основе модульной арифметики совершенный кубоид, если он существует : ^[7]

Одно ребро, две диагонали грани и диагональ пространства должны быть нечетными, одно ребро и оставшаяся диагональ грани должны делиться на 4, а оставшееся ребро должно делиться на 16.
Два ребра должны иметь длину, кратную 3, и хотя бы одно из этих ребер должно иметь длину, кратную 9.
Одно ребро должно иметь длину, кратную 5.
Одно ребро должно иметь длину, кратную 7.
Одно ребро должно иметь длину, кратную 11.
Одно ребро должно иметь длину, кратную 19.
Одно ребро или диагональ пространства должна делиться на 13.
Одно ребро, диагональ грани или диагональ пространства должны делиться на 17.
Одно ребро, диагональ грани или диагональ пространства должны делиться на 29.
Одно ребро, диагональ грани или диагональ пространства должны делиться на 37.

Кроме того:

Пространственная диагональ не является ни степенью простого числа , ни произведением двух простых чисел . ^[8]^{: с. 579}
Диагональ пространства может содержать только простые делители, равные 1 по модулю 4. ^[8]^{: с. 566}^[9]

Если существует совершенный кубоид и $a,b,c$ это его края, $d,e,f$ — соответствующие диагонали грани и диагональ пространства $g$ , затем

Треугольник с длинами сторон $(d^{2},e^{2},f^{2})$ - Геронов треугольник это площадь $abcg$ с рациональными биссектрисами. ^[10]
Остроугольный треугольник с длинами сторон $(af,be,cd)$ , тупоугольные треугольники с длинами сторон $(bf,ae,gd),(ad,cf,ge),(ce,bd,gf)$ представляют собой героновы треугольники, площадь которых равна ${\frac {abcg}{2}}$ .

Кубовидные гипотезы

Три гипотезы о кубоиде - это три математических утверждения, утверждающие о неприводимости трех одномерных многочленов с целыми коэффициентами , зависящими от нескольких целочисленных параметров. Гипотезы связаны с проблемой идеального кубоида . ^[11]^[12] Хотя они не эквивалентны задаче об идеальном кубоиде, если все эти три гипотезы верны, то идеальных кубоидов не существует. Они не доказаны и не опровергнуты.

Гипотеза о кубоиде 1. Для любых двух положительных взаимно простых целых чисел $a\neq u$ полином восьмой степени

P_{au}(t)=t^{8}+6\,(u^{2}-a^{2})\,t^{6}+(a^{4}-4\,a^{2}\,u^{2}+u^{4})\,t^{4}-6\,a^{2}\,u^{2}\,(u^{2}-a^{2})\,t^{2}+u^{4}\,a^{4}

( 1 )

неприводимо над кольцом целых чисел $\mathbb {Z}$ .

Гипотеза 2 о кубоиде. Для любых двух положительных взаимно простых целых чисел $p\neq q$ полином десятой степени

{\begin{aligned}Q_{pq}(t)={}&t^{10}+(2q^{2}+p^{2})(3q^{2}-2p^{2})t^{8}\\[4pt]&{}+(q^{8}+10p^{2}q^{6}+4p^{4}q^{4}-14p^{6}q^{2}+p^{8})t^{6}\\[4pt]&{}-p^{2}q^{2}(q^{8}-14p^{2}q^{6}+4p^{4}q^{4}+10p^{6}\,q^{2}+p^{8})t^{4}\\[4pt]&{}-p^{6}\,q^{6}\,(q^{2}+2\,p^{2})\,(-2\,q^{2}+3\,p^{2})\,t^{2}\\[4pt]&{}-q^{10}\,p^{10}\end{aligned}}

( 2 )

неприводимо над кольцом целых чисел $\mathbb {Z}$ .

Гипотеза о кубоиде 3. Для любых трёх положительных взаимно простых целых чисел $a$ , $b$ , $u$ такое, что ни одно из условий

{\begin{array}{lcr}{\text{1)}}\qquad a=b;\qquad \qquad &{\text{3)}}\qquad b\,u=a^{2};\qquad \qquad &{\text{5)}}\qquad a=u;\\{\text{2)}}\qquad a=b=u;\qquad \qquad &{\text{4)}}\qquad a\,u=b^{2};\qquad \qquad &{\text{6)}}\qquad b=u\end{array}}

( 3 )

полином двенадцатой степени

{\begin{aligned}P_{abu}(t)={}&t^{12}+(6u^{2}-2a^{2}-2b^{2})t^{10}\\&{}+(u^{4}+b^{4}+a^{4}+4a^{2}u^{2}+4b^{2}u^{2}-12b^{2}a^{2})t^{8}\\&{}+(6a^{4}u^{2}+6u^{2}b^{4}-8a^{2}b^{2}u^{2}-2u^{4}a^{2}-2u^{4}b^{2}-2a^{4}b^{2}-2b^{4}a^{2})t^{6}\\&{}+(4u^{2}b^{4}a^{2}+4a^{4}u^{2}b^{2}-12u^{4}a^{2}b^{2}+u^{4}a^{4}+u^{4}b^{4}+a^{4}b^{4})t^{4}\\&{}+(6a^{4}u^{2}b^{4}-2u^{4}a^{4}b^{2}-2u^{4}a^{2}b^{4})t^{2}+u^{4}a^{4}b^{4}.\end{aligned}}

( 4 )

неприводимо над кольцом целых чисел $\mathbb {Z}$ .

Почти идеальные кубоиды

У почти идеального кубоида 6 из 7 длин являются рациональными. Такие кубоиды можно разделить на три типа: кубоиды тела , края и грани . ^[13] В случае кубоида тела диагональ тела (пространства) $g$ иррациональна. Для реберного кубоида одно из ребер $a, b, c$ иррационально. У кубоида грани одна из диагоналей грани $d, e, f$ иррациональна.

Кубовид тела обычно называют кубоидом Эйлера в честь Леонарда Эйлера, который обсуждал этот тип кубоида. ^[14] Он также знал о кубоидах лица и привел пример (104, 153, 672). ^[15] Три целочисленные длины ребер кубоида и три целые длины диагоналей граней кубоида также можно интерпретировать как длины ребер геронова тетраэдра , который также является ортосхемой Шлефли . Существует бесконечно много лицевых кубоидов и бесконечно много героновских ортосхем. ^[16]

Наименьшие решения для каждого типа почти идеальных кубоидов, представленных в виде ребер, диагоналей граней и пространственной диагонали $(a, b, c, d, e, f, g)$ , следующие:

Кубовидная форма тела : $(44, 117, 240, 125, 244, 267, \sqrt 73225)$
Краевой кубоид : $(520, 576, \sqrt 618849, 776, 943, 975, 1105)$
Кубовидная форма лица : $(104, 153, 672, 185, 680, \sqrt 474993, 697)$

По состоянию на июль 2020 г. ^[update], найдено 167 043 кубоида с наименьшим целым ребром менее 200 000 000 027: 61 042 - кубоиды Эйлера (тела), 16 612 - кубоиды с ребром с комплексным числом длины ребра, 32 286 - реберные кубоиды и 57 103 - лицевые кубоиды. ^[17]

По состоянию на декабрь 2017 г. ^[update], исчерпывающий поиск подсчитал все кубоиды с ребрами и гранями с наименьшей диагональю целочисленного пространства менее 1 125 899 906 842 624: 194 652 были кубоидами с ребрами, 350 778 были кубоидами с гранями. ^[6]

Идеальный параллелепипед

Совершенный параллелепипед — это параллелепипед с ребрами целой длины, диагоналями граней и диагоналями тела, но не обязательно со всеми прямыми углами; идеальный кубоид — частный случай идеального параллелепипеда. В 2009 году было показано существование десятков идеальных параллелепипедов. ^[18] отвечая на открытый вопрос Ричарда Гая . Некоторые из этих идеальных параллелепипедов имеют две прямоугольные грани. Наименьший совершенный параллелепипед имеет ребра 271, 106 и 103; короткие диагонали лица 101, 266 и 255; длинные диагонали грани 183, 312 и 323; и диагонали тела 374, 300, 278 и 272.

См. также

Пифагорова четверка

Примечания

^ Jump up to: Перейти обратно: ^а ^б ^с ^д ^и Вацлав Серпинский , Треугольники Пифагора , Dover Publications, 2003 (оригинальное издание 1962 г.).
^ Видения бесконечности: Великие математические проблемы Яна Стюарта, Глава 17
^ Вайсштейн, Эрик В. «Кирпич Эйлера» . Математический мир .
^ Нилл, Оливер (24 февраля 2009 г.). «Идеальные кирпичики Эйлера в поисках сокровищ» (PDF) . Математическая таблица. Гарвардский университет .
^ Jump up to: Перейти обратно: ^а ^б ^с Мэтсон, Роберт Д. «Результаты компьютерного поиска идеального кубоида» (PDF) . unsolvedproblems.org . Проверено 24 февраля 2020 г.
^ Jump up to: Перейти обратно: ^а ^б Александр Белогуров, Распределенный поиск идеального кубоида, https://www.academia.edu/39920706/Distributed_search_for_a_perfect_cuboid
^ М. Крайчик, О некоторых рациональных кубоидах, Scripta Mathematica, том 11 (1945).
^ Jump up to: Перейти обратно: ^а ^б И. Корец, Нижние границы совершенных рациональных кубоидов, Матем. Словака, 42 (1992), № 5, с. 565-582.
^ Рональд ван Люйк, О идеальных кубоидах, июнь 2000 г.
^ Флориан Лука (2000) «Идеальные кубоиды и идеальные квадратные треугольники», журнал Mathematics, 73:5, стр. 400-401
^ Шарипов Р.А. (2012). «Совершенные кубоиды и неприводимые многочлены». Уфимский математический журнал . 4 (1): 153–160. arXiv : 1108.5348 . Бибкод : 2011arXiv1108.5348S .
^ Шарипов Р.А. (2015). «Асимптотический подход к задаче идеального кубоида» . Уфимский математический журнал . 7 (3): 100–113. дои : 10.13108/2015-7-3-95 .
^ Ратбан Р.Л., Гранлунд Т., Целочисленная таблица кубоидов с решениями типа тела, ребра и грани // Матем. Комп., 1994, Том. 62, С. 441-442.
^ Эйлер, Леонард, Полное руководство по алгебре, Императорская Академия наук, Санкт-Петербург, 1771 г.
^ Эйлер, Леонхард, Полное руководство по алгебре, 2, Часть II, 236, английский перевод: Эйлер, Элементы алгебры, Springer-Verlag 1984
^ «Задача 930» (PDF) , Решения, Mathematical Cross , 11 (5): 162–166, май 1985 г.
^ Ратбан, Рэндалл Л. (14 июля 2020 г.). «Целочисленная кубовидная таблица». arXiv : 1705.05929v4 [ math.NT ].
^ Сойер, Хорхе Ф.; Райтер, Клиффорд А. (2011). «Совершенные параллелепипеды существуют». Математика вычислений . 80 (274): 1037–1040. arXiv : 0907.0220 . дои : 10.1090/s0025-5718-2010-02400-7 . S2CID 206288198 . .

Ссылки

Пиявка, Джон (1977). «Возвращение к рациональному кубоиду». Американский математический ежемесячник . 84 (7): 518–533. дои : 10.2307/2320014 . JSTOR 2320014 .
Шаффер, Шерилл (1987). «Необходимые делители совершенных целочисленных кубоидов». Тезисы Американского математического общества . 8 (6): 440.
Гай, Ричард К. (2004). Нерешенные проблемы теории чисел . Спрингер-Верлаг . стр. 275–283. ISBN 0-387-20860-7 .
Крайчик, М. (1945). «О некоторых рациональных кубоидах». Скрипта Математика . 11 : 317–326.
Робертс, Тим (2010). «Некоторые ограничения на существование идеального кубоида». Бюллетень Австралийского математического общества . 37 : 29–31. ISSN 1326-2297 .

[Sierpinski-1] Jump up to: Перейти обратно: ^а ^б ^с ^д ^и Вацлав Серпинский , Треугольники Пифагора , Dover Publications, 2003 (оригинальное издание 1962 г.).

[2] Видения бесконечности: Великие математические проблемы Яна Стюарта, Глава 17

[3] Вайсштейн, Эрик В. «Кирпич Эйлера» . Математический мир .

[Saunderson-4] Нилл, Оливер (24 февраля 2009 г.). «Идеальные кирпичики Эйлера в поисках сокровищ» (PDF) . Математическая таблица. Гарвардский университет .

[Matson-5] Jump up to: Перейти обратно: ^а ^б ^с Мэтсон, Роберт Д. «Результаты компьютерного поиска идеального кубоида» (PDF) . unsolvedproblems.org . Проверено 24 февраля 2020 г.

[Belogourov-6] Jump up to: Перейти обратно: ^а ^б Александр Белогуров, Распределенный поиск идеального кубоида, https://www.academia.edu/39920706/Distributed_search_for_a_perfect_cuboid

[7] М. Крайчик, О некоторых рациональных кубоидах, Scripta Mathematica, том 11 (1945).

[Korec-8] Jump up to: Перейти обратно: ^а ^б И. Корец, Нижние границы совершенных рациональных кубоидов, Матем. Словака, 42 (1992), № 5, с. 565-582.

[9] Рональд ван Люйк, О идеальных кубоидах, июнь 2000 г.

[Luca-10] Флориан Лука (2000) «Идеальные кубоиды и идеальные квадратные треугольники», журнал Mathematics, 73:5, стр. 400-401

[shr_01-11] Шарипов Р.А. (2012). «Совершенные кубоиды и неприводимые многочлены». Уфимский математический журнал . 4 (1): 153–160. arXiv : 1108.5348 . Бибкод : 2011arXiv1108.5348S .

[shr_02-12] Шарипов Р.А. (2015). «Асимптотический подход к задаче идеального кубоида» . Уфимский математический журнал . 7 (3): 100–113. дои : 10.13108/2015-7-3-95 .

[13] Ратбан Р.Л., Гранлунд Т., Целочисленная таблица кубоидов с решениями типа тела, ребра и грани // Матем. Комп., 1994, Том. 62, С. 441-442.

[14] Эйлер, Леонард, Полное руководство по алгебре, Императорская Академия наук, Санкт-Петербург, 1771 г.

[15] Эйлер, Леонхард, Полное руководство по алгебре, 2, Часть II, 236, английский перевод: Эйлер, Элементы алгебры, Springer-Verlag 1984

[16] «Задача 930» (PDF) , Решения, Mathematical Cross , 11 (5): 162–166, май 1985 г.

[17] Ратбан, Рэндалл Л. (14 июля 2020 г.). «Целочисленная кубовидная таблица». arXiv : 1705.05929v4 [ math.NT ].

[18] Сойер, Хорхе Ф.; Райтер, Клиффорд А. (2011). «Совершенные параллелепипеды существуют». Математика вычислений . 80 (274): 1037–1040. arXiv : 0907.0220 . дои : 10.1090/s0025-5718-2010-02400-7 . S2CID 206288198 . .

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[17]

[18]