Эксперименты по резерфордскому рассеянию

Точная копия аппарата, который Гейгер и Марсден использовали для измерения рассеяния альфа-частиц в эксперименте 1913 года.

Эксперименты по резерфордскому рассеянию стали знаковой серией экспериментов , благодаря которым ученые узнали, что у каждого атома есть ядро весь его положительный заряд , в котором сосредоточен и большая часть его массы. Они пришли к такому выводу после измерения того, как альфа-частиц луч рассеивается , когда он ударяется о тонкую металлическую фольгу . Эксперименты были выполнены между 1906 и 1913 годами Гансом Гейгером и Эрнестом Марсденом под руководством Эрнеста Резерфорда в Физических лабораториях Манчестерского университета . Самый важный из этих экспериментов был проведен в 1909 году: в нем были обнаружены углы рассеяния, превышающие 90 градусов.

Это физическое явление было объяснено Эрнестом Резерфордом в классической статье 1911 года, которая в конечном итоге привела к широкому использованию рассеяния. в физике элементарных частиц для изучения субатомной материи. Резерфордовское рассеяние или кулоновское рассеяние — это упругое рассеяние заряженных частиц за счет кулоновского взаимодействия . Эта статья также положила начало разработке планетарной Резерфорда модели атома модели и, в конечном итоге, Бора .

Резерфордовское рассеяние теперь используется сообществом материаловедения в аналитическом методе, называемом резерфордовским обратным рассеянием .

Краткое содержание

Модель атома Томсона

« Модель сливового пудинга » атома с семью электронами, представленная Дж. Дж. Томсоном в 1905 году.

Основная статья: Модель сливового пудинга

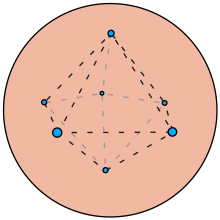
Преобладающая модель строения атома до экспериментов Резерфорда была разработана Дж. Дж. Томсоном . Томсон открыл электрон благодаря своим работам по катодным лучам. и пришел к выводу, что электрический ток — это электроны, перетекающие от одного атома к соседнему атому последовательно. Когда электрический ток отсутствует, электроны остаются внутри атомов. Чтобы объяснить, почему атомы электрически нейтральны, он предположил существование соразмерного количества положительного заряда, который уравновешивает отрицательный заряд электронов. Не имея представления о том, что является источником этого положительного заряда, он предварительно предположил, что положительный заряд находится повсюду в атоме, приняв для простоты сферическую форму. Томсон считал положительную сферу похожей на жидкость, в которой электроны могут перемещаться в ней, причем их расположение и движение определяются балансом электростатических сил.

Томсона не совсем удовлетворила эта упрощенная идея, и он надеялся отказаться от нее по мере усовершенствования своей модели. Томсону так и не удалось разработать полную и стабильную модель, которая могла бы предсказать любые другие известные свойства атома, такие как спектры излучения и валентности. Японский учёный Хантаро Нагаока отверг модель Томсона на том основании, что противоположные заряды не могут проникнуть друг в друга. Вместо этого он предположил, что электроны вращаются вокруг положительного заряда, как кольца вокруг Сатурна . Однако эта модель также была известна как нестабильная.

Альфа-частицы и атом Томсона

Альфа -частица — это невидимая положительно заряженная частица вещества, спонтанно испускаемая некоторыми радиоактивными элементами. Альфа-частицы можно обнаружить с помощью фосфоресцирующих экранов, фотопластинок или электродов. Резерфорд открыл их в 1899 году. В 1906 году, изучая, как пучки альфа-частиц отклоняются магнитными и электрическими полями, он пришел к выводу, что они, по сути, представляют собой атомы гелия, лишенные своих электронов, поскольку имеют одинаковое соотношение заряда к массе и атомный вес. Протоны и нейтроны еще не были открыты, поэтому Резерфорд ничего не знал о структуре альфа-частиц.

Модель Томсона соответствовала экспериментальным данным, доступным в то время. Томсон изучал рассеяние бета-частиц , которое показало небольшие угловые отклонения, смоделированные как взаимодействие частицы со многими последовательными атомами. Каждое взаимодействие частицы с электронами атома и положительной фоновой сферой привело бы к небольшому отклонению, но таких столкновений могло бы сложиться множество. Ожидалось, что рассеяние альфа-частиц будет аналогичным. Команда Резерфорда показала, что модель рассеяния неверна, потому что неверна модель атома.

Резерфорд, Гейгер и Марсден

Эрнест Резерфорд

Ганс Гейгер

Эрнест Марсден

Эрнест Резерфорд был профессором физики Лэнгуорси в Манчестерском университете Виктории. (ныне Манчестерский университет ). Он уже получил множество наград за исследования радиации. Он открыл существование альфа-лучей , бета-лучей и гамма-лучей и доказал, что они являются следствием распада атомов . В 1906 году его посетил немецкий физик по имени Ганс Гейгер , и он был настолько впечатлен, что попросил Гейгера остаться и помочь ему в его исследованиях. Эрнест Марсден был студентом-физиком, обучавшимся у Гейгера.

В 1908 году Резерфорд попытался самостоятельно определить заряд и массу альфа-частиц. Для этого он хотел подсчитать количество альфа-частиц и измерить их общий заряд; соотношение даст заряд одной альфа-частицы. Альфа-частицы настолько малы, что по отдельности их невозможно увидеть, но Резерфорд знал из работы Дж. С. Таунсенда в 1902 году, что альфа-частицы ионизируют молекулы воздуха, и если воздух находится в сильном электрическом поле, каждый ион будет производить каскад ионов, дающих импульс. электрического тока. На этом принципе Резерфорд и Гейгер разработали простое счетное устройство, состоящее из двух электродов в стеклянной трубке. (См. эксперимент № 1908. ) Каждая альфа-частица, прошедшая через трубку, создавала электрический импульс, который можно было посчитать. Это была ранняя версия счетчика Гейгера .

Счетчик, построенный Гейгером и Резерфордом, оказался ненадежным, поскольку альфа-частицы слишком сильно отклонялись при столкновениях с молекулами воздуха внутри камеры обнаружения. Сильно меняющиеся траектории альфа-частиц означали, что не все они генерировали одинаковое количество ионов при прохождении через газ, что приводило к ошибочным показаниям. Это озадачило Резерфорда, поскольку он считал, что альфа-частицы слишком тяжелы, чтобы их можно было так сильно отклонить. Резерфорд попросил Гейгера выяснить, насколько далеко материя может рассеивать альфа-лучи.

Эксперименты, которые они разработали, включали бомбардировку металлической фольги пучком альфа-частиц, чтобы наблюдать, как фольга рассеивает их в зависимости от ее толщины и материала. Они использовали фосфоресцентный экран для измерения траекторий частиц. Каждое попадание альфа-частицы на экран вызывало крошечную вспышку света. Гейгер часами работал в затемненной лаборатории, подсчитывая эти крошечные сцинтилляции с помощью микроскопа. Для изготовления металлической фольги они тестировали различные металлы, но отдали предпочтение золоту , поскольку фольгу можно было сделать очень тонкой, поскольку золото — самый ковкий металл. В качестве источника альфа-частиц Резерфорд выбрал вещество радон — вещество, в несколько миллионов раз более радиоактивное, чем уран.

Теория рассеяния и новая модель атома

Слева: Если бы модель Томсона была верна, все альфа-частицы должны были бы пройти через фольгу с минимальным рассеянием.
Справа: Гейгер и Марсден наблюдали, что небольшая часть альфа-частиц испытывает сильное отклонение.

Они обнаружили, что металлическая фольга может рассеивать некоторые альфа-частицы во всех направлениях, иногда более чем на 90°. Согласно модели Томсона, это должно было быть невозможно; он основан на рассеянии электронов, а электроны слишком легки, чтобы повернуть более тяжелую альфа-частицу в сторону. Это заставило Резерфорда пересмотреть модель атома. В новой модели Резерфорда положительная сфера по крайней мере в 10 000 раз меньше, чем предполагал Томсон: она заполняет не весь объем атома, а крошечное ядро ​​и окружена облаком электронов, которое заполняет больший объем атома. атом. Согласно закону Кулона , большинство частиц вообще не попадают в это компактное ядро, но когда они приближаются, сила становится очень сильной. Это ядро ​​с положительным зарядом также несет в себе всю массу, которую не переносят электроны, то есть почти всю ее. Закрепленное таким образом своей большой массой ядро ​​может очень сильно отклонить пролетящую альфа-частицу, если эта частица подойдет достаточно близко.

Чтобы проверить свою модель, Резерфорд разработал научную модель, позволяющую предсказать интенсивность альфа-частиц под разными углами, которые они рассеивают, выходящих из золотой фольги, предполагая, что весь положительный заряд сосредоточен в центре атома. Он также показал, что модель рассеяния Томсона неадекватна для объяснения наблюдений Гейгера и Марсдена. Эта работа была опубликована в его ныне знаменитом Статья 1911 года «Рассеяние α- и β-частиц веществом и структура атома».

Наследие

В первые годы на теперь уже знаменитую статью Резерфорда 1911 года не было никакой реакции. Статья была в основном посвящена рассеянию альфа-частиц в эпоху, когда рассеяние частиц не стало основным инструментом физики. Вероятностные методы, которые он использовал, и запутанный набор наблюдений не сразу убедили его.

Ядерная физика

Основные статьи: Ядерная физика и рассеяние

В камере Вильсона трек альфа-частицы с энергией 5,3 МэВ от ²¹⁰ Источник Pb (1) испытывает резерфордовское рассеяние (2), отклоняясь на угол около 30°. Он снова рассеивается (3) и, наконец, останавливается в газе. Ядро-мишень отскакивает, оставляя короткий след (2). (шкала см)

Первые последствия заключались в том, что они побудили обратить внимание на эксперименты по рассеянию. Например, первые результаты работы камеры Вильсона , полученные Ч.ТР. Уилсоном, показывают рассеяние альфа-частиц и также появились в 1911 году. Со временем рассеяние частиц стало основным аспектом теоретической и экспериментальной физики; Концепция Резерфорда о «поперечном сечении» теперь доминирует в описаниях экспериментальной физики элементарных частиц. Историк Сильван С. Швебер предполагает, что подход Резерфорда ознаменовал переход к рассмотрению всех взаимодействий и измерений в физике как процессов рассеяния. После ядра — термин, введенный Резерфордом в 1912 году. — стала общепринятой моделью ядра атома, анализ Резерфорда рассеяния альфа-частиц создал новую ветвь физики — ядерную физику.

Атомная модель

Основные статьи: модель Резерфорда и модель Резерфорда – Бора.

Даже новая модель атома Резерфорда не вызвала никакого переполоха. Резерфорд явно игнорирует электроны, упоминая только Хантаро Нагаоки , сатурнианскую модель в которой электроны вращаются вокруг крошечного «солнца», модель, которая ранее была отвергнута как механически нестабильная. Игнорируя электроны, Резерфорд также игнорирует любые потенциальные последствия атомной спектроскопии для химии. Сам Резерфорд не настаивал на своей атомной модели: в его собственной книге 1913 года «Радиоактивные вещества и их излучения» атом упоминается только дважды; другие книги других авторов того же времени посвящены модели Томсона.

Влияние ядерной модели Резерфорда произошло после того, как Нильс Бор прибыл в Манчестер в качестве аспиранта по приглашению Резерфорда. Бор отказался от своей работы над моделью Томсона в пользу ядерной модели Резерфорда, развивая модель Резерфорда-Бора в течение следующих нескольких лет. В конечном итоге Бор включил ранние идеи квантовой механики в модель атома, что позволило предсказать электронные спектры и концепции химии.

Хантаро Нагаока , который когда-то предложил сатурнианскую модель атома, писал Резерфорду из Токио в 1911 году: «Я был поражен простотой аппарата, который вы используете, и блестящими результатами, которые вы получаете». Астроном Артур Эддингтон назвал открытие Резерфорда самым важным научным достижением с тех пор, как Демокрит предложил атом. С тех пор Резерфорда называют «отцом ядерной физики».

В лекции, прочитанной 15 октября 1936 года в Кембриджском университете, Резерфорд описал свое потрясение результатами эксперимента 1909 года :

Затем я помню, как два или три дня спустя Гейгер пришел ко мне в большом волнении и сказал: «Нам удалось заставить некоторые α-частицы двигаться назад…». Это было совершенно невероятное событие, которое когда-либо случалось со мной в моей жизни. Это было почти так же невероятно, как если бы вы выпустили 15-дюймовый снаряд в кусок папиросной бумаги, а он вернулся и поразил вас. Поразмыслив, я понял, что это рассеяние назад должно быть результатом одиночного столкновения, и когда я произвел расчеты, я увидел, что невозможно получить что-либо такого порядка, если не взять систему, в которой большая часть массы атома сконцентрировалось в крошечном ядре. Именно тогда у меня возникла идея атома с крошечным массивным центром, несущего заряд.

Приведенный выше текст часто цитируется в учебниках с описанием экспериментов. Заявление Резерфорда о неожиданности является хорошей историей, но ко времени эксперимента Гейгера-Мардсена результат подтвердил подозрения, которые Резерфорд развил в своих многочисленных предыдущих экспериментах.

Эксперименты

Рассеяние альфа-частиц: эксперименты 1906 и 1908 годов

В 1906 году Резерфорд заметил, что альфа-частицы, проходя через листы слюды, отклоняются ими на целых 2 градуса. Резерфорд поместил радиоактивный источник в герметичную трубку с узкими щелями, за которой следовала фотопластинка. Половина щели была покрыта тонким слоем слюды. Магнитное поле вокруг трубки менялось каждые 10 минут, чтобы исключить влияние бета-лучей, которые, как известно, чувствительны к магнитным полям. Трубку вакуумировали в различных объемах и записывали серию изображений. При самом низком давлении изображение открытой щели было четким, тогда как изображения покрытой слюдой щели или открытой щели при более высоких давлениях были нечеткими. Резерфорд объяснил эти результаты рассеянием альфа-частиц. в статье, опубликованной в 1906 г. Он уже понимал значение этого наблюдения для моделей атомов: «такой результат ясно показывает тот факт, что атомы материи должны быть местом действия очень мощных электрических сил».

Этот аппарат был описан в статье Ганса Гейгера в 1908 году. Он мог измерить отклонения лишь на несколько градусов.

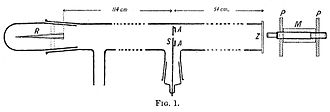
В статье Гейгера 1908 года « О рассеянии α-частиц веществом » описывается следующий эксперимент. Он сконструировал длинную стеклянную трубку длиной почти два метра. На одном конце трубки находилось некоторое количество « эманации радия » (R), служившей источником альфа-частиц. Противоположный конец трубки был закрыт фосфоресцирующим экраном (Z). В середине трубки имелась щель шириной 0,9 мм. Альфа-частицы от R прошли через щель и создали на экране светящееся пятно света. С помощью микроскопа (М) подсчитывали сцинтилляции на экране и измеряли их распространение. Гейгер откачал из трубки весь воздух, чтобы альфа-частицы беспрепятственно проходили, и они оставляли на экране аккуратное и плотное изображение, соответствующее форме щели. Затем Гейгер впустил в трубку немного воздуха, и светящееся пятно стало более рассеянным. Затем Гейгер откачал воздух и накрыл щель АА металлической фольгой, золотой или алюминиевой. Это также привело к тому, что пятно света на экране стало более рассеянным. Этот эксперимент продемонстрировал, что и воздух, и твердое вещество могут заметно рассеивать альфа-частицы.

Отражение альфа-частицы: эксперимент 1909 года

Результаты первоначальных экспериментов по рассеянию альфа-частиц были запутанными. Угловой разброс частицы на экране сильно менялся в зависимости от формы аппарата и его внутреннего давления. Резерфорд предложил Эрнесту Марсдену, студенту-физику, обучающемуся у Гейгера, искать диффузно отраженные или обратно рассеянные альфа-частицы, хотя их и не ожидалось. Первый грубый рефлектор Марсдена дал результаты, поэтому Гейгер помог ему создать более сложный аппарат. Им удалось продемонстрировать, что 1 из 8000 столкновений альфа-частиц было диффузным отражением. Хотя эта доля была небольшой, она была намного больше, чем могла объяснить модель атома Томсона. Это привело к критическому эксперименту, опубликованному в 1909 году.

В этих экспериментах наблюдалось, как альфа-частицы, испускаемые радиоактивным источником (А), отражаются от металлического отражателя (R) и попадают на флуоресцентный экран (S) на другой стороне свинцовой пластины (P).

В статье 1909 года « О диффузном отражении α-частиц » Гейгер и Марсден описали эксперимент, в котором они доказали, что альфа-частицы действительно могут рассеиваться более чем на 90°. В своем эксперименте они подготовили небольшую коническую стеклянную трубку (AB), содержащую «эманацию радия» ( радон ), «радий А» (настоящий радий) и «радий С» ( висмут -214); его открытый конец запечатан слюдой . Это был их излучатель альфа-частиц. Затем они установили свинцовую пластину (P), за которой поместили флуоресцентный экран (S). Трубка располагалась на противоположной стороне пластины так, чтобы испускаемые ею альфа-частицы не могли напрямую ударить по экрану. Они заметили на экране несколько мерцаний, поскольку некоторые альфа-частицы обходили пластину, отскакивая от молекул воздуха. Затем они поместили металлическую фольгу (R) сбоку от свинцовой пластины. Они тестировали свинец, золото, олово, алюминий, медь, серебро, железо и платину. Они направили трубку на фольгу, чтобы посмотреть, отскочат ли от нее альфа-частицы и ударятся ли об экран на другой стороне пластины, и наблюдали увеличение количества сцинтилляций на экране. Подсчитав сцинтилляции, они заметили, что металлы с более высокой атомной массой, такие как золото, отражают больше альфа-частиц, чем более легкие, такие как алюминий.

Затем Гейгер и Марсден захотели оценить общее количество отражаемых альфа-частиц. Предыдущая установка была непригодна для этого, поскольку трубка содержала несколько радиоактивных веществ (радий плюс продукты его распада) и, следовательно, испускаемые альфа-частицы имели разные радиусы действия , а также потому, что им было трудно определить, с какой скоростью трубка испускает альфа-частицы. . На этот раз они поместили небольшое количество радия C (висмута-214) на свинцовую пластину, который отразился от платинового отражателя (R) и попал на экран. Они пришли к выводу, что примерно 1 из 8000 альфа-частиц, попавших в отражатель, отразилась на экране. По сравнению с огромным количеством альфа-частиц, которые беспрепятственно проходят через металлическую фольгу, такое небольшое количество отражений под большим углом было странным результатом.

Зависимость от материала и толщины фольги: эксперимент 1910 г.

Этот аппарат был описан Гейгером в статье 1910 года. Он был разработан для точного измерения того, как рассеяние меняется в зависимости от материала и толщины фольги.

Газета 1910 года Гейгер, «Рассеяние α-частиц материей» , описывает эксперимент, с помощью которого он стремился измерить, как наиболее вероятный угол отклонения альфа-частицы зависит от материала, через который она проходит, толщины этого материала и толщины материала. скорость альфа-частиц. Он сконструировал герметичную стеклянную трубку, из которой откачивался воздух. На одном конце находилась лампочка (Б), содержащая «эманации радия» ( радон -222). С помощью ртути радон из Б закачивался в узкую стеклянную трубку, конец которой в А был заткнут слюдой . На другом конце трубки находился флуоресцентный экран из сульфида цинка (S). Микроскоп, который он использовал для подсчета сцинтилляций на экране, был прикреплен к вертикальной миллиметровой шкале с нониусом, что позволяло Гейгеру точно измерять места появления на экране вспышек света и таким образом рассчитывать углы отклонения частиц. Альфа-частицы, испускаемые из точки A, сужались до пучка небольшим круглым отверстием в точке D. Гейгер поместил металлическую фольгу на пути лучей в точках D и E, чтобы наблюдать, как изменилась зона вспышек. Он испытал золото, олово, серебро, медь и алюминий. Он также мог изменять скорость альфа-частиц, помещая дополнительные листы слюды или алюминия в точку А.

На основании проведенных им измерений Гейгер пришел к следующим выводам:

• наиболее вероятный угол отклонения увеличивается с толщиной материала
• наиболее вероятный угол отклонения пропорционален атомной массе вещества
• наиболее вероятный угол отклонения уменьшается с увеличением скорости альфа-частиц

Статья Резерфорда «Структура атома» (1911 г.)

Основная статья: Резерфордовское рассеяние

Принимая во внимание результаты вышеупомянутых экспериментов, Резерфорд в 1911 году опубликовал знаковую статью под названием «Рассеяние α- и β-частиц веществом и структура атома», в которой он показал, что однократное рассеяние на очень маленьком и интенсивном электрическом заряде предсказывает в первую очередь небольшие -угловое рассеяние с небольшим, но измеримым обратным рассеянием. Для целей своих математических расчетов он предположил, что этот центральный заряд положителен, но признал, что не может это доказать и что ему пришлось ждать других экспериментов, чтобы развить свою теорию.

Резерфорд разработал математическое уравнение, которое моделировало, как фольга должна рассеивать альфа-частицы, если весь положительный заряд и большая часть атомной массы сосредоточены в точке в центре атома.

$$s={\frac {Xnt\cdot \csc ^{4}{\frac {\phi }{2}}}{16r^{2}}}\cdot {\left({\frac {2q_{n}q_{a}}{mv^{2}}}\right)}^{2}$$

• s = количество альфа-частиц, падающих на единицу площади под углом отклонения Φ
• r = расстояние от точки падения α-лучей на рассеивающий материал.
• X = общее количество частиц, падающих на рассеивающий материал
• n = количество атомов в единице объема материала
• t = толщина фольги
• q _n = положительный заряд атомного ядра
• q _a = положительный заряд альфа-частиц
• m = масса альфа-частицы
• v = скорость альфа-частицы

По данным рассеяния Резерфорд оценил центральный заряд q _n примерно в +100 единиц.

В статье Резерфорда не обсуждается какое-либо расположение электронов, кроме обсуждения рассеяния в Дж. Дж. Томсона и модели сливового пудинга в Хантаро Нагаоки . модели Сатурна Он показывает, что результаты рассеяния, предсказанные моделью Томсона, также объясняются однократным рассеянием, но модель Томсона не объясняет рассеяние на большие углы. Он говорит, что модель Нагаоки, имеющая компактный заряд, согласуется с данными рассеяния. Сатурнианская модель ранее была отвергнута по другим причинам. Так называемая резерфордовская модель атома с вращающимися электронами не была предложена Резерфордом в статье 1911 года.

Подтверждение теории рассеяния: эксперимент 1913 года

В статье 1913 года « Законы отклонения α-частиц на большие углы » Гейгер и Марсден описывают серию экспериментов, с помощью которых они пытались экспериментально проверить приведенное выше уравнение, разработанное Резерфордом. Уравнение Резерфорда предсказало, что количество сцинтилляций в минуту , которые будут наблюдаться под данным углом Φ, должно быть пропорционально:

1. косек ⁴ ⁠ Φ / 2 ⁠
2. толщина фольги т
3. величина квадрата центрального заряда Q _n
4. ⁠ 1 / ( мв ² ) ² ⁠

В их статье 1913 года описаны четыре эксперимента, с помощью которых они доказали каждое из этих четырех отношений.

Этот аппарат был разработан для точного измерения картины рассеяния альфа-частиц, создаваемых металлической фольгой (F). Микроскоп (М) и экран (S) были прикреплены к вращающемуся цилиндру и могли совершать полный круг вокруг фольги.

Чтобы проверить, как рассеяние меняется в зависимости от угла отклонения (т.е. если s ∝ csc ⁴ ⁠ Φ / 2 ⁠ ). Гейгер и Марсден построили аппарат, который представлял собой полый металлический цилиндр, установленный на поворотном столе. Внутри цилиндра находилась металлическая фольга (F) и источник излучения, содержащий радон (R), установленный на отдельной колонне (Т), которая позволяла цилиндру вращаться независимо. Колонка также представляла собой трубку, по которой воздух откачивался из цилиндра. Микроскоп (М) с объективом, закрытым флуоресцентным экраном из сульфида цинка (S), проникал через стенку цилиндра и направлялся на металлическую фольгу. Они тестировали серебряную и золотую фольгу. Повернув стол, микроскоп можно было пройти полный круг вокруг фольги, что позволило Гейгеру наблюдать и подсчитывать альфа-частицы, отклоненные на угол до 150°. Исправив экспериментальную ошибку, Гейгер и Марсден обнаружили, что число альфа-частиц, отклоненных на заданный угол Φ, действительно пропорционально csc. ⁴ ⁠ Φ / 2 ⁠ .

С помощью этого аппарата было измерено изменение картины рассеяния в зависимости от толщины фольги, атомного веса материала и скорости альфа-частиц. Вращающийся диск в центре имел шесть отверстий, которые можно было закрыть фольгой.

Затем Гейгер и Марсден проверили, как рассеяние меняется в зависимости от толщины фольги (т.е. если s ∝ t ). Они сконструировали диск (S) с просверленными в нем шестью отверстиями. Отверстия были закрыты металлической фольгой (F) различной толщины или не покрыты ею для контроля. Затем этот диск был запечатан в латунное кольцо (А) между двумя стеклянными пластинами (В и С). Диск можно было вращать с помощью стержня (P), чтобы каждое окно оказалось перед источником альфа-частиц (R). На заднем стекле располагался экран из сульфида цинка (Z). Гейгер и Марсден обнаружили, что количество сцинтилляций, появляющихся на экране из сульфида цинка, действительно было пропорционально толщине, пока эта толщина была небольшой.

Гейгер и Марсден повторно использовали вышеупомянутый прибор, чтобы измерить, как картина рассеяния меняется в зависимости от квадрата заряда ядра (т.е. если s ∝ Q _n ² ). Гейгер и Марсден не знали, каков положительный заряд ядра их металлов (они только что открыли, что ядро ​​вообще существует), но предполагали, что он пропорционален атомному весу, поэтому они проверяли, пропорционально ли рассеяние атомный вес в квадрате. Гейгер и Марсден закрыли отверстия диска фольгой из золота, олова, серебра, меди и алюминия. Они измерили останавливающую способность каждого крыла, приравняв его к эквивалентной толщине воздуха. Они подсчитали количество сцинтилляций в минуту, которые каждая фольга производит на экране. Они разделили количество сцинтилляций в минуту на воздушный эквивалент соответствующей фольги, а затем снова разделили на квадратный корень из атомного веса (Гейгер и Марсден знали, что для фольг с одинаковой тормозной способностью число атомов на единицу площади пропорционально квадратный корень из атомного веса). Таким образом, для каждого металла Гейгер и Марсден получили количество сцинтилляций, которое производит фиксированное число атомов. Затем для каждого металла они разделили это число на квадрат атомного веса и обнаружили, что соотношения более или менее одинаковы. Тем самым они доказали, что s ∝ Q _н ² .

Наконец, Гейгер и Марсден проверили, как рассеяние меняется в зависимости от скорости альфа-частиц (т.е. если s ∝ ⁠ 1 / v ⁴ ⁠ ). Снова используя тот же аппарат, они замедлили альфа-частицы, поместив дополнительные листы слюды перед источником альфа-частиц. Они обнаружили, что в пределах экспериментальной ошибки число мерцаний действительно пропорционально ⁠ 1 / v ⁴ ⁠ .

Положительный заряд ядра: 1913 г.

В своей статье 1911 года ( см. выше ) Резерфорд предположил, что центральный заряд атома положителен, но отрицательный заряд также хорошо соответствовал бы его модели рассеяния. В статье 1913 г. Резерфорд заявил, что «ядро» (как он теперь его называл) действительно заряжено положительно, основываясь на результатах экспериментов по изучению рассеяния альфа-частиц в различных газах.

В 1917 году Резерфорд и его помощник Уильям Кей начали исследовать прохождение альфа-частиц через такие газы, как водород и азот. В этом эксперименте они пропустили луч альфа-частиц через водород и осторожно поместили свой детектор — экран из сульфида цинка — сразу за пределами диапазона альфа-частиц, которые были поглощены газом. Тем не менее они уловили какие-то заряженные частицы, вызывающие мерцания на экране. Резерфорд интерпретировал это как альфа-частицы, сбивающие ядра водорода вперед в направлении луча, а не назад.

Атомная модель в решающей статье Резерфорда 1911 года.

Резерфорд начинает свою статью 1911 года. с обсуждением результатов Томсона о рассеянии бета-частиц , форме радиоактивности, которая приводит к образованию электронов с высокой скоростью. В модели Томсона электроны циркулировали внутри сферы с положительным зарядом. Резерфорд подчеркивает необходимость составного или многократного рассеяния: отклонения, предсказанные для каждого столкновения, составляют намного меньше одного градуса. Затем он предлагает модель, которая будет вызывать большие отклонения при одном столкновении: поместите весь положительный заряд в центр сферы и игнорируйте рассеяние электронов как незначительное. Концентрированный заряд объяснит, почему большинство альфа-частиц вообще не рассеиваются – они вообще пропускают заряд – и тем не менее частицы, которые попадают в центр, рассеиваются на большие углы.

Оценка максимального размера ядра

Резерфорд начинает свой анализ с рассмотрения лобового столкновения альфа-частицы и атома. Это установит минимальное расстояние между ними, значение, которое будет использоваться в его расчетах.

Предполагая отсутствие внешних сил и первоначально альфа-частицы находятся далеко от ядра, закон обратных квадратов между зарядами альфа-частицы и ядра дает потенциальную энергию, приобретаемую частицей по мере ее приближения к ядру. При лобовых столкновениях альфа-частицы с ядром вся кинетическая энергия альфа-частицы превращается в потенциальную энергию , и частица останавливается и поворачивает назад.

Схематическое изображение лобового столкновения альфа-частицы с атомом на минимальном расстоянии сильно преувеличено.

Там, где частица останавливается, расстояние $r_{\text{min}}$ потенциальная энергия соответствует исходной кинетической энергии:

$${\frac {1}{2}}mv^{2}=k{\frac {q_{1}q_{2}}{r_{\text{min}}}}$$

где

$$k={\frac {1}{4\pi \epsilon _{0}}}$$

Перестановка: $$r_{\text{min}}=k{\frac {2q_{1}q_{2}}{mv^{2}}}$$

Для альфа-частицы:

• м (масса) = 6,644 24 × 10 ⁻²⁷ кг = 3,7273 × 10 ⁹ эВ/ c ²
• q ₁ (для гелия) = 2× 1,6 × 10 ⁻¹⁹ С = 3,2 × 10 ⁻¹⁹ С
• q ₂ (для золота) = 79× 1,6 × 10 ⁻¹⁹ С = 1,27 × 10 ⁻¹⁷ С
• v (начальная скорость) = 2 × 10 ⁷ м/с (для этого примера)

Расстояние от альфа-частицы до центра ядра ( rmin _{) в} этой точке является верхним пределом радиуса ядра.Подстановка их дает значение около 2,7 × 10 ⁻¹⁴ м , или 27 фм . (Истинный радиус составляет около 7,3 фм.) Истинный радиус ядра не восстанавливается в этих экспериментах, поскольку альфа-частицы не имеют достаточно энергии, чтобы проникнуть на расстояние более 27 фм от ядерного центра, как уже отмечалось, когда фактический радиус ядра составляет около 7,3 фм. золото 7,3 фм.

Рис. 1. Диаграмма потенциальной энергии для модели атома Резерфорда, иллюстрирующая концентрацию в ядре.

Статья Резерфорда 1911 года начал с немного другой формулы, подходящей для лобового столкновения со сферой с положительным зарядом:

$${\frac {1}{2}}mv^{2}=NeE\cdot \left({\frac {1}{b}}-{\frac {3}{2R}}+{\frac {b^{2}}{2R^{3}}}\right)$$

В обозначениях Резерфорда e — элементарный заряд , N — зарядовое число ядра (теперь мы знаем, что оно равно атомному номеру), а E — заряд альфа-частицы. Во времена Резерфорда принято было измерять заряд в электростатических единицах , расстояние в сантиметрах, силу в динах и энергию в эргах . В настоящее время принято измерять заряд в кулонах , расстояние в метрах, силу в ньютонах и энергию в джоулях . Резерфорд использовал $b$ как расстояние до точки поворота (названное r _min выше ), а R — радиус атома. Первый член — это кулоновское отталкивание, использованное выше. Эта форма предполагает, что альфа-частица может проникнуть через положительный заряд. На момент публикации статьи Резерфорда модель сливового пудинга Томсона предполагала наличие положительного заряда с радиусом атома, в тысячи раз превышающим значение r _min, найденное выше. На рис. 1 показано, насколько сконцентрирован этот потенциал по сравнению с размером атома.Многие результаты Резерфорда выражаются через расстояние r _min до точки поворота , что упрощает результаты и ограничивает потребность в единицах расчета этой точки поворота.

Однократное рассеяние на тяжелых ядрах

Из своих результатов по лобовому столкновению Резерфорд знает, что рассеяние альфа-частиц происходит вблизи центра атома, на радиусе, в 10 000 раз меньшем радиуса атома. Поэтому он игнорирует эффект «отрицательного электричества» (то есть электронов). Более того, он начинает с предположения об отсутствии потери энергии при столкновении, то есть игнорирует отдачу атома-мишени. Позже в своей статье он вернется к каждому из этих вопросов. В этих условиях альфа-частица и атом взаимодействуют через центральную силу — физическую проблему, впервые изученную Исааком Ньютоном . Центральная сила действует только вдоль линии между частицами, и когда сила изменяется пропорционально обратному квадрату, как в данном случае сила Кулона , была разработана подробная теория под названием « проблема Кеплера» . Хорошо известные решения проблемы Кеплера называются орбитами , а несвязанные орбиты — гиперболами .Так, Резерфорд предположил, что альфа-частица будет двигаться по гиперболической траектории под действием силы отталкивания вблизи центра атома, как показано на рис. 1.

Рис. 1. Геометрия формулы рассеяния Резерфорда, основанная на диаграмме из его статьи 1911 года. Альфа-частица представляет собой зеленую точку и движется по красной траектории, которая представляет собой гиперболу с O в центре и S в качестве внешнего фокуса. Атомное ядро ​​расположено в точке S. А — это апсида , точка наибольшего сближения. b — прицельный параметр, латеральное расстояние между начальной траекторией альфа-частицы и ядром.

Чтобы применить решения для гиперболических траекторий к проблеме альфа-частиц, Резерфорд выражает параметры гиперболы через геометрию рассеяния и энергии.Он начинает с сохранения углового момента . Когда частица массы $m$ и скорость $v_{0}$ находится далеко от атома, его момент импульса вокруг центра атома будет равен $mbv_{0}$ где $b$ — прицельный параметр , который представляет собой поперечное расстояние между траекторией альфа-частицы и атомом. В точке наибольшего сближения, обозначенной А на рис. 1, угловой момент будет равен $mr_{A}v_{A}$. Поэтому

$$mbv_{0}=mr_{A}v_{A}$$

$$v_{A}={\frac {bv_{0}}{r_{A}}}$$

Мы одновременно рассматриваем закон сохранения энергии между теми же двумя точками:

$${\tfrac {1}{2}}mv_{0}^{2}={\tfrac {1}{2}}mv_{A}^{2}+{\frac {kq_{a}q_{g}}{r_{A}}}$$

Левая часть и первый член правой части представляют собой кинетические энергии частицы в двух точках; последний член представляет собой потенциальную энергию, обусловленную силой Кулона между альфа-частицей и атомом в точке наибольшего сближения (А). qa _— заряд альфа-частицы, qg _— заряд ядра, k — постоянная Кулона .

Тогда уравнение энергии можно переписать следующим образом:

$$v_{A}^{2}=v_{0}^{2}\left(1-{\frac {kq_{a}q_{g}}{{\tfrac {1}{2}}mv_{0}^{2}r_{A}}}\right)$$

Для удобства негеометрические физические переменные в этом уравнении можно содержать в переменной $r_{\text{min}}$, которая является точкой наибольшего сближения в сценарии лобового столкновения, который был рассмотрен в предыдущем разделе этой статьи:

$$r_{\text{min}}={\frac {kq_{a}q_{g}}{{\tfrac {1}{2}}mv_{0}^{2}}}$$

Это позволяет Резерфорду упростить уравнение энергии до:

$$v_{A}^{2}=v_{0}^{2}\left(1-{\frac {r_{\text{min}}}{r_{A}}}\right)$$

Это оставляет нам два одновременных уравнения для $v_{A}^{2}$, первое получено из уравнения сохранения импульса, а второе - из уравнения сохранения энергии. С их помощью мы можем устранить $v_{A}$ и $v_{0}$ и придем к новой формуле $r_{\text{min}}$:

$$v_{A}^{2}={\frac {b^{2}v_{0}^{2}}{r_{A}^{2}}}=v_{0}^{2}\left(1-{\frac {r_{\text{min}}}{r_{A}}}\right)$$

$$r_{\text{min}}=r_{A}-{\frac {b^{2}}{r_{A}}}$$

Следующий шаг – найти формулу для $r_{A}$. Из рис. 1, $r_{A}$ представляет собой сумму двух расстояний, связанных с гиперболой, SO и OA. Эти расстояния можно выразить через угол $\Phi$ и ударный параметр $b$.

Рис. 2. Основные составляющие геометрии гипербол .

Эксцентриситет гиперболы — это величина, описывающая форму гиперболы. Его можно рассчитать, разделив фокусное расстояние на длину большой полуоси, которая согласно рис. 1 равна ⁠ СО / ОА ⁠ . Эксцентриситет также равен $\sec \Phi$, где $\Phi$ – угол между большой осью и асимптотой, который, как видно на рис. 1, является пределом $\varphi$. Вместе они дают:

$${\frac {\text{SO}}{\text{OA}}}=\sec \Phi$$

Как следует из рис. 1, фокусное расстояние SO равно

$${\text{SO}}=b\csc \Phi$$

и поэтому

$${\text{OA}}={\frac {\text{SO}}{\sec \Phi }}=b\cot \Phi$$

Имея эти формулы для SO и OA, мы теперь можем найти формулу для $r_{A}$. Расстояние $r_{A}$ можно записать в терминах $\Phi$ используя формулу половинного угла :

$$r_{A}={\text{SO}}+{\text{OA}}=b\csc \Phi +b\cot \Phi =b\cot {\frac {\Phi }{2}}$$

Используя предыдущее уравнение для $r_{A}$ теперь мы можем найти связь между физическими и геометрическими переменными:

$$r_{\text{min}}=r_{A}-{\frac {b^{2}}{r_{A}}}$$

$$=b\cot {\frac {\Phi }{2}}-{\frac {b^{2}}{b\cot {\frac {\Phi }{2}}}}$$

$$=b{\frac {\cot ^{2}{\frac {\Phi }{2}}-1}{\cot {\frac {\Phi }{2}}}}$$

$$=2b\cot \Phi$$

где на последнем этапе используется формула котангенса двойного угла .

Угол рассеяния частицы $\theta =\pi -2\Phi$ и поэтому $\Phi ={\tfrac {\pi -\theta }{2}}$. С помощью известной формулы отражения связь между θ и b становится следующей:

$$r_{\text{min}}=2b\cot \left({\frac {\pi -\theta }{2}}\right)$$

$$=2b\tan {\frac {\theta }{2}}$$

$$\cot {\frac {\theta }{2}}={\frac {2b}{r_{\text{min}}}}$$

который можно переставить, чтобы дать

$$\theta =2\arctan {\frac {r_{\text{min}}}{2b}}=2\arctan \left({\frac {kq_{a}q_{g}}{bmv_{0}^{2}}}\right)$$

Гиперболические траектории рассеяния альфа-частиц на ядре Золота (современный радиус показан серым кружком), описанные в статье Резерфорда 1911 года.

Резерфорд приводит некоторые иллюстративные значения, показанные в этой таблице:

Таблица углов отклонения Резерфорда

$b/r_{\text{min}}$	10	5	2	1	0.5	0.25	0.125
$\theta$	5.7°	11.4°	28°	53°	90°	127°	152°

Подход Резерфорда к этой проблеме рассеяния остается стандартным подходом в учебниках. по классической механике .

Интенсивность против угла

Геометрия дифференциального сечения рассеяния

Для сравнения с экспериментами взаимосвязь между прицельным параметром и углом рассеяния необходимо преобразовать в зависимость вероятности от угла. Сечение рассеяния дает относительную интенсивность по углам: $${\frac {d\sigma }{d\Omega }}(\Omega )d\Omega ={\frac {{\text{number of particles scattered into solid angle }}d\Omega {\text{ per unit time}}}{\text{incident intensity}}}$$

В классической механике угол рассеяния Θ однозначно определяет начальную кинетическую энергию налетающих частиц и прицельный параметр p . Следовательно, количество частиц, рассеянных под углом между Θ и Θ + d Θ, должно быть таким же, как количество частиц с соответствующими прицельными параметрами между p и p + dp . Для интенсивности инцидента I это означает: $$2\pi Ip\left|dp\right|=-2\pi \sigma (\Theta )I\sin(\Theta )d\Theta$$ Таким образом, сечение зависит от угла рассеяния как: $$\sigma (\Theta )=-{\frac {p}{\sin \Theta }}{\frac {dp}{d\Theta }}$$ Использование прицельного параметра как функции угла p (Θ) из приведенного выше результата однократного рассеяния дает сечение резерфордовского рассеяния: $$\sigma (\Theta )={\frac {1}{4}}\left({\frac {Z_{1}Z_{2}e^{2}}{2E}}\right)^{2}{\frac {1}{\sin ^{4}{\frac {\Theta }{2}}}}.$$

Сечение резерфордовского рассеяния имеет сильный пик около нуля градусов, но имеет ненулевые значения вплоть до 180 градусов.

Эта формула предсказала результаты, которые Гейгер измерил в следующем году. Вероятность рассеяния на малые углы значительно превышает вероятность на большие углы, отражая крошечное ядро, окруженное пустым пространством. Однако в редких случаях близкого сближения рассеяние на большие углы происходит только с одной целью.

В конце разработки формулы сечения Резерфорд подчеркивает, что результаты применимы к однократному рассеянию и, следовательно, требуют измерений с тонкой фольгой. Для тонких фольг величина рассеяния пропорциональна толщине фольги, что согласуется с измерениями Гейгера.

Сравнение с результатами Дж. Дж. Томсона

На момент публикации статьи Резерфорда Дж. Дж. Томсон был «бесспорным мировым мастером в конструировании атомов». Резерфорду нужно было сравнить свой новый подход с подходом Томсона. Модель Томсона, представленная в 1910 году. смоделировал столкновения электронов с гиперболическими орбитами из своей статьи 1906 года. в сочетании с фактором положительной сферы. Множественные результирующие небольшие отклонения, усугубленные с помощью случайного блуждания .

В своей статье Резерфорд подчеркивал, что одно только рассеяние могло бы объяснить результаты Томсона, если положительный заряд был сосредоточен в центре.Резерфорд вычисляет вероятность однократного рассеяния на компактном заряде и показывает, что она в 3 раза превышает вероятность многократного рассеяния Томсона. Резерфорд завершает свой анализ, включая влияние плотности и толщины фольги, а затем приходит к выводу, что тонкая фольга определяется однократным, а не многократным рассеянием.

Более поздний анализ показал, что модель рассеяния Томсона не может объяснить большое рассеяние.Максимальные угловые отклонения от рассеяния электронов или от положительной сферы составляют менее 0,02°; даже множество таких событий рассеяния в совокупности приведет к среднему отклонению менее одного градуса и вероятности рассеяния на 90 ° менее одного из 10. ³⁵⁰⁰ .

Целевая отдача

Анализ Резерфорда предполагал, что траектории альфа-частиц поворачиваются в центре атома, но скорость выхода не уменьшается. Это эквивалентно предположению, что сконцентрированный заряд в центре имел бесконечную массу или был закреплен на месте. Резерфорд обсуждает ограничения этого предположения, сравнивая рассеяние на более легких атомах, таких как алюминий, и более тяжелых атомах, таких как золото. Если концентрированный заряд легче, он отскочит от взаимодействия, набирая импульс, в то время как альфа-частица теряет импульс и, следовательно, замедляется.

Современные методы анализируют этот тип кулоновского рассеяния в центре системы отсчета. Шесть координат двух частиц (также называемых «телами») преобразуются в три относительные координаты между двумя частицами и три координаты центра масс, движущихся в пространстве (называемые лабораторной системой координат). Взаимодействие происходит только в относительных координатах, что дает эквивалентную задачу одного тела. точно так же, как решил Резерфорд, но с разными интерпретациями массы и угла рассеяния.

Вместо массы альфа-частицы более точная формула, включающая отдачу, использует приведенную массу : $$\mu ={\cfrac {m_{1}m_{2}}{m_{1}+m_{2}}}.$$ Для резерфордовского рассеяния альфа-частицы на золоте с массой 197 приведенная масса очень близка к массе альфа-частицы: $$\mu _{\text{Au}}={\cfrac {4\times 197}{4+197}}=3.92\approx 4.$$Для более легкого алюминия с массой 27 эффект больше: $$\mu _{\text{Au}}={\cfrac {4\times 27}{4+27}}=3.48,$$разница в массе 13%. Резерфорд отмечает эту разницу и предлагает провести эксперименты с более легкими атомами.

Второй эффект — изменение угла рассеяния. Угол в относительной системе координат или системе координат центра масс необходимо преобразовать в угол в лабораторной системе координат. В лабораторной системе координат, обозначенной индексом L, угол рассеяния для общего центрального потенциала равен $$\tan \Theta _{L}={\frac {\sin \Theta }{\cos \Theta +(m_{1}/m_{2})}}.$$ Для тяжелой частицы, такой как золото, использованной Резерфордом, $m_{1}/m_{2}=4/197\approx 0.02\ll 1$ и почти во всех ракурсах этим фактором можно пренебречь: лабораторный и относительный углы одинаковы, $\Theta _{L}\approx \Theta$.

Изменение угла рассеяния изменяет формулу дифференциального сечения, необходимую для сравнения с экспериментом. Для любого центрального потенциала дифференциальное сечение в лабораторной системе координат связано с сечением в системе центра масс соотношением $${\frac {d\sigma }{d\Omega }}_{L}={\frac {\left(1+2s\cos \Theta +s^{2}\right)^{3/2}}{1+s\cos \Theta }}{\frac {d\sigma }{d\Omega }}$$где $s=m_{1}/m_{2}.$

Альтернативный метод определения угла рассеяния

В статье Резерфорда 1911 года использовались решения по гиперболической орбите для задачи центральной силы обратных квадратов, разработанные со времен Исаака Ньютона и доступные в учебниках эпохи Резерфорда, например, ссылка. Затем Резерфорд показывает, как эта орбита связывает параметр удара частицы с углом отклонения и как это можно использовать для прогнозирования экспериментальных данных зависимости интенсивности от угла для его модели атома. Связь между прицельным параметром и углом отклонения также может быть получена непосредственно с помощью механики Ньютона.

В этом разделе используются следующие переменные и значения для альфа-частицы, проходящей мимо ядра атома золота:

• q _g = положительный заряд атома золота = 79 e = 1,26 × 10 ⁻¹⁷ С
• q _a = заряд альфа-частицы = 2 e = 3,20 × 10 ⁻¹⁹ С
• v = скорость альфа-частицы = 1,53 × 10 ⁷ РС
• m = масса альфа-частицы = 6,64 × 10 ⁻²⁷ кг
• k = постоянная Кулона = 8,987 × 10 ⁹ Н·м ² /С ²

Геометрия рассеяния показана на этой диаграмме.

Прицельный параметр b — это расстояние между начальной траекторией альфа-частицы и параллельной линией, проходящей через ядро. Меньшие значения b приближают частицу к атому, поэтому она ощущает большую силу отклонения, что приводит к большему углу отклонения θ . Цель состоит в том, чтобы найти связь между b и углом отклонения.

Путь альфа-частицы представляет собой гиперболу, а чистое изменение импульса $\Delta {\vec {P}}$ проходит вдоль оси симметрии. Судя по геометрии на диаграмме и величине векторов начального и конечного импульса, $|{\vec {P}}_{i}|=|{\vec {P}}_{f}|=mv$, величина $\Delta {\vec {P}}$ может быть связано с углом отклонения:

$$\Delta P=2mv\cdot \sin {\frac {\theta }{2}}.$$

Вторая формула для $\Delta P$ включение b даст связь с углом отклонения. Чистое изменение импульса также можно найти, добавляя небольшие приращения к импульсу на всем протяжении траектории, используя интеграл

$$\Delta P=\int \limits _{0}^{\infty }{\frac {kq_{a}q_{g}}{r^{2}}}\cdot \cos \varphi \cdot \mathrm {\mathrm {d} } t$$

где $r$ - расстояние между альфа-частицей и центром ядра и $\varphi$ — его угол от оси симметрии. Эти две являются полярными координатами альфа-частицы в момент времени. $t$.Здесь кулоновская сила, действующая вдоль линии между альфа-частицей и атомом, равна ${\frac {kq_{a}q_{g}}{r^{2}}}$и фактор $\cos \varphi$ дает ту часть силы, которая вызывает отклонение.

Полярные координаты r и φ зависят от t в интеграле, но они должны быть связаны друг с другом, поскольку обе изменяются по мере движения частицы. Изменение переменной и пределов интегрирования с t на φ делает эту связь явной:

$$\Delta P=\int \limits _{-{\frac {\pi -\theta }{2}}}^{\frac {\pi -\theta }{2}}{\frac {kq_{a}q_{g}}{r^{2}}}\cdot \cos \varphi \cdot {\frac {\mathrm {d} t}{\mathrm {d} \varphi }}\cdot \mathrm {d} \varphi$$

Фактор $dt/d\varphi =1/\omega$ является обратной величиной угловой скорости частицы. Поскольку сила действует только вдоль линии между частицей и атомом, угловой момент , пропорциональный угловой скорости, постоянен: $$mvb=mr^{2}\omega =mr^{2}{\frac {\mathrm {d} \varphi }{\mathrm {d} t}}$$Этот закон сохранения углового момента дает формулу для $dt/d\varphi$:

$${\frac {\mathrm {d} t}{\mathrm {d} \varphi }}={\frac {r^{2}}{vb}}$$

Замена $dt/d\varphi$ в интеграле для ∆ P одновременно устраняет зависимость от r :

$$\Delta P=\int \limits _{-{\frac {\pi -\theta }{2}}}^{\frac {\pi -\theta }{2}}{\frac {kq_{a}q_{g}}{vb}}\cdot \cos \varphi \cdot \mathrm {d} \varphi$$

$$={\frac {kq_{a}q_{g}}{vb}}\left(\sin \left[{\frac {\pi -\theta }{2}}\right]-\sin \left[-{\frac {\pi -\theta }{2}}\right]\right)$$

Применение тригонометрических тождеств $\sin({\tfrac {\pi }{2}}-\theta )=\cos \theta$ и $\sin(\theta \pm {\tfrac {\pi }{2}})=\pm \cos \theta$ для упрощения этого результата дает вторую формулу для $\Delta P$:

$$\Delta P={\frac {kq_{a}q_{g}}{vb}}\cdot 2\cos {\frac {\theta }{2}}=2mv\cdot \sin {\frac {\theta }{2}}$$Решение для θ как функции от b дает окончательный результат

$$\theta =2\arctan \left({\frac {kq_{a}q_{g}}{bmv^{2}}}\right)$$

Вычисляя формулу прицельного параметра b , равного радиусу ядра золота, 7 × 10 ⁻¹⁵ m дает угол отклонения θ равный 2,56 радиан (147°). Если вместо этого использовать радиус атома золота 1,44 × 10. ⁻¹⁰ м приводит к небольшому углу отклонения θ, составляющему 0,0003 радиана (0,02 °).

См. также

• Атомная теория
• Спектроскопия резерфордовского обратного рассеяния
• Список экспериментов по рассеянию

Библиография

• «Ядерный мир Резерфорда: история открытия ядра» . Американский институт физики . Проверено 23 октября 2014 г.
• «Резерфордовское рассеяние» . Гиперфизика . Государственный университет Джорджии . Проверено 13 августа 2014 г.
• Артур Бейзер (1969). Перспективы современной физики . Книжная компания МакГроу-Хилл.
• «Гейгер и Марсден» . Кавендишская лаборатория . Архивировано из оригинала 6 октября 2014 г. Проверено 23 июля 2014 г.
• Джон Дэйнтит; Дерек Джертсен (1999). Словарь ученых . Издательство Оксфордского университета . ISBN  978-0-19-280086-2 .
• Майкл Фаулер. «Резерфордовское рассеяние» . Конспект лекций по физике 252 . Университет Вирджинии . Проверено 23 июля 2014 г.
• Ганс Гейгер (1908). «О рассеянии α-частиц веществом» . Труды Лондонского королевского общества А. 81 (546): 174–177. Бибкод : 1908RSPSA..81..174G . дои : 10.1098/rspa.1908.0067 .
• Ганс Гейгер; Эрнест Марсден (1909). «О диффузном отражении α-частиц» . Труды Лондонского королевского общества А. 82 (557): 495–500. Бибкод : 1909RSPSA..82..495G . дои : 10.1098/rspa.1909.0054 .
• Ганс Гейгер (1910). «Рассеяние α-частиц веществом» . Труды Лондонского королевского общества А. 83 (565): 492–504. Бибкод : 1910RSPSA..83..492G . дои : 10.1098/rspa.1910.0038 .
• Ганс Гейгер; Эрнест Марсден (1913). «Законы отклонения α-частиц на большие углы» (PDF) . Философский журнал . Серия 6. 25 (148): 604–623. дои : 10.1080/14786440408634197 .
• Джон Л. Хейлброн (январь 1968 г.). «Рассеяние α- и β-частиц и атома Резерфорда». Архив истории точных наук . 4 (4): 247–307. дои : 10.1007/BF00411591 .
• Джон Л. Хейлброн (2003). Эрнест Резерфорд и взрыв атомов . Издательство Оксфордского университета . ISBN  978-0-19-512378-4 .
• Джон В. Джуэтт младший; Раймонд А. Сервей (2014). «Ранние модели атома». Физика для ученых и инженеров с современной физикой (9-е изд.). Брукс/Коул. п. 1299.
• Радостные манеры (2000). Квантовая физика: Введение . ЦРК Пресс. ISBN  978-0-7503-0720-8 .
• Хантаро Нагаока (1904). «Кинетика системы частиц, иллюстрирующая линейный и полосовой спектр и явления радиоактивности» . Философский журнал . Серия 6. 7 (41): 445–455. дои : 10.1080/14786440409463141 .
• Ричард Ривз (2008). Сила природы: пограничный гений Эрнеста Резерфорда . WW Norton & Co. ISBN  978-0-393-07604-2 .
• Эрнест Резерфорд (1899). «Урановое излучение и производимая им электропроводность» (PDF) . Философский журнал . 47 (284): 109–163.
• Эрнест Резерфорд (1911). «Рассеяние α- и β-частиц веществом и структура атома» (PDF) . Философский журнал . Серия 6. 21 (125): 669–688. дои : 10.1080/14786440508637080 .
• Эрнест Резерфорд (1906). «Масса и скорость α-частиц, вылетевших из радия и актиния» . Философский журнал . Серия 6. 12 (70): 348–371. дои : 10.1080/14786440609463549 .
• Эрнест Резерфорд (1912). «Происхождение β и γ-лучей из радиоактивных веществ» . Философский журнал . Серия 6. 24 (142): 453–462. дои : 10.1080/14786441008637351 .
• Эрнест Резерфорд; Джон Митчелл Наттал (1913). «Рассеяние α-частиц газами» . Философский журнал . Серия 6. 26 (154): 702–712. дои : 10.1080/14786441308635014 .
• Эрнест Резерфорд (1914). «Строение атома» . Философский журнал . Серия 6. 27 (159): 488–498. дои : 10.1080/14786440308635117 .
• Эрнест Резерфорд (1938). «Сорок лет физики» . В Нидхэме, Джозеф; Пейджел, Уолтер (ред.). Предыстория современной науки: десять лекций в Кембридже, организованных Комитетом по истории науки в 1936 году . Издательство Кембриджского университета .
• Эрнест Резерфорд (1913). Радиоактивные вещества и их излучения . Издательство Кембриджского университета .
• Эрнест Резерфорд (1936). «Радиоактивность и атомная структура». Журнал Химического общества . 1936 : 508–516. дои : 10.1039/JR9360000508 .
• Дж. А. Кроутер (1910). «О рассеянии однородных β-лучей и количестве электронов в атоме» . Труды Лондонского королевского общества . А. 84 ​​(570): 226–247.
• Джозеф Дж. Томсон (1904). «О строении атома: исследование стабильности и периодов колебаний ряда корпускул, расположенных через равные промежутки по окружности круга; с применением результатов к теории атомного строения» . Философский журнал . Ряд 6. 7 (39): 237. doi : 10.1080/14786440409463107 .
• Джей Джей Томсон (1906). «О количестве частиц в атоме» (PDF) . Философский журнал . 6. 11 (66): 769–781. дои : 10.1080/14786440609463496 .
• Гэри Тиббетс (2007). Как рассуждали великие учёные: научный метод в действии . Эльзевир . ISBN  978-0-12-398498-2 .
• Артур Стюарт Ева (1939). Резерфорд: жизнь и письма RT. Достопочтенный. Лорд Резерфорд, О.М. Макмиллан.
• Жан Перрен (1910) [1909]. Броуновское движение и молекулярная реальность . Перевод Ф. Содди. Тейлор и Фрэнсис.
• Э.А. Дэвис; Эй Джей Фалконер (1997). Дж. Дж. Томсон и открытие электрона . Тейлор и Фрэнсис. ISBN  0-7484-0720-0 .
• Гиора Хон; Бернард Р. Гольдштейн (6 сентября 2013 г.). «Атомная модель сливового пудинга Дж. Дж. Томсона: создание научного мифа» . Аннален дер Физик . 525 (8–9): А129–А133. Бибкод : 2013АнП...525А.129Х . дои : 10.1002/andp.201300732 .
• Джей Джей Томсон (1907). Корпускулярная теория материи . Сыновья Чарльза Скрибнера.
• Гольдштейн, Герберт ; Пул, Чарльз; Сафко, Джон (2002). Классическая механика (третье изд.). Аддисон-Уэсли. ISBN  978-0-201-65702-9 .
• Тонг, Дэвид. «Лекции по динамике и относительности» . Кембриджский университет . Проверено 14 июля 2024 г. | Глава 4 Центральные силы

Внешние ссылки

• Описание эксперимента с сайта cambridgephysicals.org.