Преобразование Хафа
| Обнаружение функций |
|---|
| Обнаружение края |
| Обнаружение угла |
| Обнаружение больших двоичных объектов |
| Обнаружение гребней |
| Преобразование Хафа |
| Тензор структуры |
| Обнаружение аффинных инвариантных функций |
| Описание функции |
| Масштабировать пространство |
— Преобразование Хафа это метод выделения признаков, используемый в анализе изображений , компьютерном зрении , распознавании образов и цифровой обработке изображений . [ 1 ] [ 2 ] Целью метода является поиск несовершенных экземпляров объектов внутри определенного класса форм с помощью процедуры голосования. Эта процедура голосования осуществляется в пространстве параметров , из которого получаются кандидаты на объекты в виде локальных максимумов в так называемом аккумуляторном пространстве, явно построенном алгоритмом вычисления преобразования Хафа.
Классическое преобразование Хафа было связано с идентификацией линий на изображении, но позже преобразование Хафа было расширено до идентификации положений произвольных форм, чаще всего кругов или эллипсов . Преобразование Хафа в том виде, в котором оно повсеместно используется сегодня, было изобретено Ричардом Дудой и Питером Хартом в 1972 году, которые назвали его «обобщенным преобразованием Хафа». [ 3 ] после соответствующего патента Пола Хафа 1962 года. [ 4 ] [ 5 ] Преобразование было популяризировано в компьютерного зрения сообществе Даной Х. Баллард в журнальной статье 1981 года под названием « Обобщение преобразования Хафа для обнаружения произвольных форм ».
История
[ редактировать ]Первоначально он был изобретен для машинного анализа фотографий пузырьковой камеры (Hough, 1959).
Преобразование Хафа было запатентовано под номером 3 069 654 в 1962 году и передано Комиссии по атомной энергии США под названием «Метод и средства распознавания сложных закономерностей». В этом патенте используется параметризация пересечения наклона для прямых линий, что неловко приводит к неограниченному пространству преобразования, поскольку наклон может достигать бесконечности.
Широко используемая сегодня параметризация ро-тета была впервые описана в
- Дуда, Р.О.; Харт, ЧП (январь 1972 г.). «Использование преобразования Хафа для обнаружения линий и кривых на изображениях» . Комм. АКМ . 15 :11–15. дои : 10.1145/361237.361242 . S2CID 1105637 .
хотя это уже было стандартом для преобразования Радона , по крайней мере, с 1930-х годов.
Вариант О'Гормана и Клоуза описан в
- О'Горман, Фрэнк; Клоуз, МБ (1976). «Нахождение краев изображения посредством коллинеарности характерных точек». IEEE Транс. Вычислить . 25 (4): 449–456. дои : 10.1109/TC.1976.1674627 . S2CID 10851078 .
Рассказ о том, как была изобретена современная форма преобразования Хафа, изложен в
- Харт, ЧП (ноябрь 2009 г.). «Как было изобретено преобразование Хафа» (PDF) . Журнал обработки сигналов IEEE . 26 (6): 18–22. дои : 10.1109/msp.2009.934181 . S2CID 16245096 . Архивировано из оригинала (PDF) 16 мая 2018 г.
Теория
[ редактировать ]При автоматизированном анализе цифровых изображений часто возникает подзадача обнаружения простых форм, таких как прямые линии, круги или эллипсы. Во многих случаях детектор краев можно использовать в качестве этапа предварительной обработки для получения точек изображения или пикселей изображения, которые находятся на желаемой кривой в пространстве изображения. Однако из-за несовершенства данных изображения или детектора границ на нужных кривых могут отсутствовать точки или пиксели, а также пространственные отклонения между идеальной линией/кругом/эллипсом и зашумленными точками края, поскольку они получены из детектор края. По этим причинам часто бывает нетривиально сгруппировать извлеченные ребра в соответствующий набор линий, кругов или эллипсов. Цель преобразования Хафа — решить эту проблему, сделав возможным группировку краевых точек в объекты-кандидаты путем выполнения явной процедуры голосования над набором параметризованных объектов изображения (Шапиро и Стокман, 304).
Обнаружение линий
[ редактировать ]Самый простой случай преобразования Хафа — обнаружение прямых линий. В общем, прямая y = mx + b может быть представлена как точка ( b , m ) в пространстве параметров. Однако вертикальные линии создают проблему. Они привели бы к неограниченным значениям параметра наклона m . Таким образом, по вычислительным причинам Дуда и Харт [ 6 ] предложил использовать нормальную форму Гессе
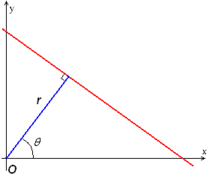
где - расстояние от начала координат до ближайшей точки на прямой, а это угол между ось и линия, соединяющая начало координат с ближайшей точкой.
Интуиция этой формы, как и уравнения плоскости, заключается в том, что каждый вектор на прямой должен быть перпендикулярен (ортогонален) прямой линии длины это исходит из истока. Видно, что точка пересечения функциональной линии и перпендикуляра, идущего из начала координат, находится в точке . Итак, для любой точки на линии вектор должен быть ортогональным вектору . Следовательно, мы получаем это для любой точки на функциональной линии уравнение должен быть удовлетворен. Поэтому, . С и , мы получаем . С , мы получаем окончательный вид .
Таким образом, каждой строке изображения можно сопоставить пару . Плоскость иногда называют пространством Хафа для множества прямых линий в двух измерениях. Такое представление делает преобразование Хафа концептуально очень близким к двумерному преобразованию Радона . Фактически, преобразование Хафа математически эквивалентно преобразованию Радона, но эти два преобразования имеют разные вычислительные интерпретации, традиционно связанные с ними. [ 7 ]
Учитывая одну точку на плоскости, набор всех прямых, проходящих через эту точку, соответствует синусоидальной кривой в плоскости ( r , θ ), которая уникальна для этой точки. Набор из двух или более точек, образующих прямую линию, создаст синусоиды, пересекающиеся в точках ( r , θ ) этой линии. Таким образом, задача обнаружения коллинеарных точек может быть преобразована в задачу поиска совпадающих кривых .
Вероятностная интерпретация
[ редактировать ]Учитывая форму, параметризованную , принимая значения из множества называемое пространством форм, преобразование Хафа можно интерпретировать как обратное преобразование распределения вероятностей в пространстве изображений в пространство форм. и интерпретировать обнаружение формы как оценку максимального правдоподобия .
Явно преобразование Хафа выполняет приблизительный наивный вывод Байеса . Начнем с однородного априора в пространстве форм. Мы рассматриваем только положительные свидетельства и игнорируем все отрицательные свидетельства, чтобы мы могли обнаружить частично закрытые формы.
Мы суммируем логарифмическое правдоподобие в пространстве форм до аддитивной константы. Предположение наивного Байеса означает, что все пиксели в пространстве изображения предоставляют независимые доказательства, так что их вероятности умножаются, то есть их логарифмические вероятности складываются. Свобода аддитивной константы позволяет нам не выполнять никаких операций с «фоновыми пикселями» в пространстве фигур.
Наконец, мы выполняем оценку максимального правдоподобия, выбирая пики логарифмического правдоподобия в пространстве форм. [ 8 ]
Выводы
Выполнение
[ редактировать ]линейного преобразования Хафа Алгоритм оценивает два параметра, которые определяют прямую линию. Пространство преобразования имеет два измерения, и каждая точка в пространстве преобразования используется в качестве аккумулятора для обнаружения или идентификации строки, описываемой выражением . Каждая точка обнаруженных краев изображения вносит свой вклад в аккумуляторы.
Размерность значения аккумулятора равна числу неизвестных параметров, т. е. двум, учитывая квантованные и в паре . Для каждого пикселя в и его окрестности алгоритм преобразования Хафа определяет, достаточно ли доказательств наличия прямой линии в этом пикселе. Если да, то он рассчитает параметры этой строки, затем найдите ячейку аккумулятора, в которую попадают параметры, и увеличьте значение этой ячейки.
Находя интервалы с самыми высокими значениями, обычно путем поиска локальных максимумов в аккумуляторном пространстве, можно извлечь наиболее вероятные линии и прочитать их (приблизительные) геометрические определения (Шапиро и Стокман, 304). Самый простой способ найти эти пики — применить тот или иной порог, но другие методы могут дать лучшие результаты в разных обстоятельствах — определить, какие линии найдены, а также сколько. Поскольку возвращаемые строки не содержат никакой информации о длине, на следующем этапе часто необходимо определить, какие части изображения каким строкам соответствуют. Более того, из-за ошибок несовершенства на этапе обнаружения границ обычно возникают ошибки в аккумуляторном пространстве, что может затруднить поиск подходящих пиков и, следовательно, подходящих линий.
Конечным результатом линейного преобразования Хафа является двумерный массив (матрица), аналогичный аккумулятору: одно измерение этой матрицы представляет собой квантованный угол. , а другое измерение — это квантованное расстояние . Каждый элемент матрицы имеет значение, равное сумме точек или пикселей, расположенных на линии, представленной квантованными параметрами. . Таким образом, элемент с наибольшим значением указывает на прямую линию, которая наиболее представлена на входном изображении. [ 9 ]
Примеры
[ редактировать ]Пример 1
[ редактировать ]Рассмотрим три точки данных, показанные здесь в виде черных точек.

- Для каждой точки данных нанесено несколько линий, проходящих через нее, все под разными углами. Здесь они показаны разными цветами.
- Преобразование Хафа накапливает вклады всех пикселей обнаруженного края. Для каждой прямой существует опорная линия, перпендикулярная ей и пересекающая начало координат . В каждом случае один из них показан стрелкой.
- Рассчитывается длина (т. е. расстояние по перпендикуляру к началу координат) и угол каждой опорной линии. Длины и углы указаны в таблице под диаграммами.
Из расчетов видно, что в том и другом случае опорная линия под углом 60° имеет одинаковую длину. Следовательно, понятно, что соответствующие линии (синие на рисунке выше) очень похожи. Таким образом, можно предположить, что все точки лежат близко к синей линии.
Пример 2
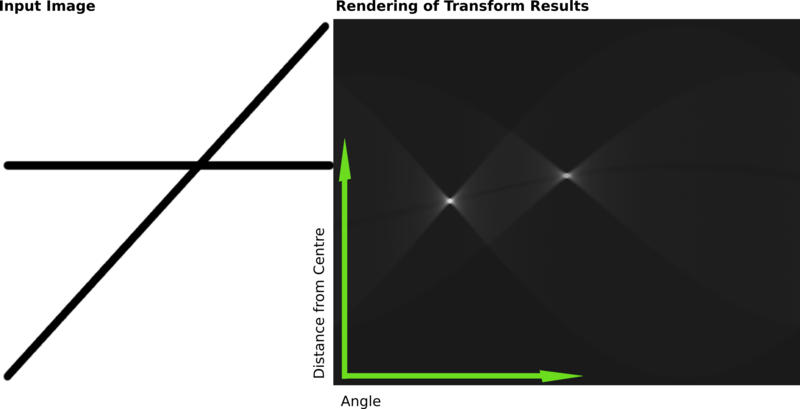
[ редактировать ]Ниже приведен другой пример, показывающий результаты преобразования Хафа на растровом изображении, содержащем две толстые линии.
Результаты этого преобразования были сохранены в матрице. Значение ячейки представляет количество кривых, проходящих через любую точку. Более высокие значения ячеек отображаются ярче. Два отчетливо ярких пятна — это параметры Хафа двух линий. По положениям этих пятен можно определить угол и расстояние от центра изображения двух линий входного изображения.
Вариации и расширения
[ редактировать ]Использование направления градиента для уменьшения количества голосов
[ редактировать ]Усовершенствование, предложенное О'Горманом и Клоузом, можно использовать для обнаружения линий, если принять во внимание, что локальный градиент интенсивности изображения обязательно будет ортогональным краю. Поскольку обнаружение границ обычно включает в себя вычисление величины градиента интенсивности, направление градиента часто обнаруживается как побочный эффект. Если данная точка с координатами ( x,y ) действительно находится на линии, то локальное направление градиента дает параметр θ , соответствующий указанной линии, и r затем немедленно получается параметр . (Шапиро и Стокман, 305) Направление градиента можно оценить с точностью до 20°, что сокращает кривую синусоиды с полных 180° примерно до 45°. Это сокращает время вычислений и дает интересный эффект, заключающийся в уменьшении количества бесполезных голосов, тем самым улучшая видимость пиков, соответствующих реальным линиям на изображении.
Преобразование Хафа на основе ядра (KHT)
[ редактировать ]Фернандеш и Оливейра [ 10 ] предложил улучшенную схему голосования для преобразования Хафа, которая позволяет программной реализации достигать производительности в реальном времени даже на относительно больших изображениях (например, 1280×960). Преобразование Хафа на основе ядра использует то же самое параметризация, предложенная Дудой и Хартом, но работает с кластерами примерно коллинеарных пикселей. Для каждого кластера голоса подаются с использованием ориентированного эллиптического ядра Гаусса, которое моделирует неопределенность, связанную с наиболее подходящей линией по отношению к соответствующему кластеру. Такой подход не только значительно повышает производительность схемы голосования, но также обеспечивает более чистый аккумулятор и делает преобразование более устойчивым к обнаружению ложных линий.
Трехмерное преобразование Хафа на основе ядра для обнаружения плоскостей (3DKHT)
[ редактировать ]Лимбергер и Оливейра [ 11 ] предложил детерминированный метод обнаружения плоскостей в неорганизованных облаках точек, стоимость которого составляет в количестве выборок, обеспечивая производительность в реальном времени для относительно больших наборов данных (до точек на процессоре с частотой 3,4 ГГц). Он основан на стратегии быстрого голосования с преобразованием Хафа для плоских областей, вдохновленной преобразованием Хафа на основе ядра (KHT). Это трехмерное преобразование Хафа на основе ядра (3DKHT) использует быстрый и надежный алгоритм для сегментации кластеров примерно копланарных выборок и голосует за отдельные кластеры (а не за отдельные выборки) на ( ) сферический аккумулятор с использованием трехмерного ядра Гаусса. Этот подход на несколько порядков быстрее, чем существующие (недетерминированные) методы обнаружения плоскостей в облаках точек, такие как RHT и RANSAC , и лучше масштабируется в зависимости от размера наборов данных. Его можно использовать с любым приложением, требующим быстрого обнаружения плоских объектов в больших наборах данных.
Преобразование Хафа кривых и его обобщение для аналитических и неаналитических форм.
[ редактировать ]Хотя описанная выше версия преобразования применима только для поиска прямых линий, аналогичное преобразование можно использовать для поиска любой формы, которая может быть представлена набором параметров. Например, круг можно преобразовать в набор из трех параметров, представляющих его центр и радиус, так что пространство Хафа станет трехмерным. Таким способом также можно найти произвольные эллипсы и кривые, а также любую форму, которую легко выразить как набор параметров.
Обобщение преобразования Хафа для обнаружения аналитических форм в пространствах любой размерности было предложено Фернандесом и Оливейрой. [ 12 ] В отличие от других подходов к аналитическим формам, основанных на преобразовании Хафа, метод Фернандеса не зависит ни от формы, которую нужно обнаружить, ни от типа входных данных. Обнаружение можно привести к аналитической форме, изменив предполагаемую модель геометрии, в которой были закодированы данные (например, евклидово пространство , проективное пространство , конформная геометрия и т. д.), в то время как предлагаемая формулировка остается неизменной. Кроме того, он гарантирует, что предполагаемые формы будут представлены с наименьшим возможным количеством параметров, и позволяет одновременно обнаруживать различные типы фигур, которые лучше всего соответствуют входному набору записей с разными размерностями и разными геометрическими определениями (например, одновременное обнаружение плоскостей и сфер, которые лучше всего соответствуют набору точек, прямых и окружностей).
Для более сложных форм на плоскости (т. е. форм, которые невозможно представить аналитически в некотором двумерном пространстве), обобщенное преобразование Хафа [ 13 ] используется, что позволяет функции голосовать за определенное положение, ориентацию и/или масштабирование формы с использованием предопределенной справочной таблицы. Преобразование Хафа накапливает вклады от всех пикселей обнаруженного края.
Процесс обнаружения круга
[ редактировать ]Изменить алгоритм для обнаружения круглых форм вместо линий относительно просто.
- Сначала мы создаем аккумуляторное пространство, которое состоит из ячейки для каждого пикселя. Первоначально каждая ячейка имеет значение 0.
- Для каждой краевой точки (i, j) изображения увеличьте все ячейки, которые согласно уравнению окружности может быть центром круга. Эти ячейки обозначены буквой в уравнении.
- Для каждого возможного значения найденный на предыдущем шаге, найдите все возможные значения которые удовлетворяют уравнению.
- Поиск локальных максимумов в аккумуляторном пространстве. Эти ячейки представляют собой круги, обнаруженные алгоритмом.
Если мы заранее не знаем радиус круга, который пытаемся найти, мы можем использовать трехмерное аккумуляторное пространство для поиска кругов с произвольным радиусом. Естественно, это более затратно в вычислительном отношении.
Этот метод также может обнаруживать круги, которые частично находятся за пределами пространства аккумулятора, если внутри него все еще присутствует достаточная площадь круга.
Обнаружение 3D-объектов (плоскости и цилиндры)
[ редактировать ]Преобразование Хафа также можно использовать для обнаружения трехмерных объектов в данных диапазона или трехмерных облаках точек . Расширение классического преобразования Хафа для обнаружения плоскостей довольно просто. Плоскость представляется ее явным уравнением для чего мы можем использовать трехмерное пространство Хафа, соответствующее , и . Это расширение страдает от тех же проблем, что и его 2D-аналог, т. е. можно надежно обнаружить почти горизонтальные плоскости, в то время как производительность ухудшается, когда плоское направление становится вертикальным (большие значения и усиливать шум в данных). Эта формулировка самолета использовалась для обнаружения самолетов в облаках точек, полученных в результате воздушного лазерного сканирования. [ 14 ] и работает очень хорошо, потому что в этой области все плоскости почти горизонтальны.
Для обобщенного обнаружения плоскости с использованием преобразования Хафа плоскость может быть параметризована ее вектором нормали. (с использованием сферических координат) и его расстояние от начала координат в результате получается трехмерное пространство Хафа. Это приводит к тому, что каждая точка входных данных голосует за синусоидальную поверхность в пространстве Хафа. Пересечение этих синусоидальных поверхностей указывает на наличие плоскости. [ 15 ] Более общий подход для более чем трех измерений требует, чтобы эвристика поиска оставалась осуществимой. [ 16 ]
Преобразование Хафа также использовалось для поиска цилиндрических объектов в облаках точек с использованием двухэтапного подхода. На первом этапе определяется ориентация цилиндра, а на втором — положение и радиус. [ 17 ]
Использование взвешенных функций
[ редактировать ]Одна распространенная вариационная деталь. То есть поиск интервалов с наибольшим количеством значений на одном этапе можно использовать для ограничения диапазона значений, искомых на следующем этапе.
Тщательно выбранное пространство параметров
[ редактировать ]Многомерное пространство параметров для преобразования Хафа не только медленное, но и, если оно реализовано без предусмотрительности, может легко переполнить доступную память. Даже если среда программирования позволяет выделять массив, превышающий доступное пространство памяти, через виртуальную память, количество необходимых для этого свопов страниц будет очень требовательным, поскольку массив аккумуляторов используется в случайном порядке и редко останавливается в непрерывной памяти. поскольку он переходит от индекса к индексу.
Рассмотрим задачу поиска эллипсов на изображении размером 800x600. Если предположить, что радиусы эллипсов ориентированы вдоль главных осей, пространство параметров будет четырехмерным. ( x , y ) определяет центр эллипса, а a и b обозначают два радиуса. Разрешение центру находиться в любом месте изображения добавляет ограничение 0<x<800 и 0<y<600. Если радиусам присвоить те же значения, что и ограничениям, останется редко заполненный массив аккумуляторов, содержащий более 230 миллиардов значений.
Задуманная таким образом программа вряд ли сможет выделить достаточно памяти. Это не означает, что проблема не может быть решена, а лишь то, что необходимо найти новые способы ограничения размера аккумуляторной батареи, что делает ее осуществимой. Например:
- Если разумно предположить, что каждый эллипс полностью содержится в изображении, диапазон радиусов можно уменьшить. Максимальный радиус может быть, если центр эллипса находится в центре изображения, что позволяет краям эллипса растягиваться до краев. В этом крайнем случае каждый из радиусов может составлять только половину размера изображения, ориентированного в одном направлении. Уменьшение диапазона a и b таким образом уменьшает массив аккумуляторов до 57 миллиардов значений.
- Поменяйте точность на пространство при оценке центра: если прогнозируется, что центр будет отклоняться на 3 по осям x и y, это уменьшит размер массива аккумуляторов примерно до 6 миллиардов значений.
- Поменяйте точность на пространство при оценке радиусов: если каждый из радиусов оценивается на 5, происходит дальнейшее уменьшение размера массива аккумуляторов примерно на 256 миллионов значений.
- Обрезайте изображение до интересующих областей. Это зависит от изображения и, следовательно, непредсказуемо, но представьте себе случай, когда все интересующие края изображения находятся в верхнем левом квадранте этого изображения. В этом случае массив аккумуляторов можно сократить еще больше, ограничив все 4 параметра коэффициентом 2, что дает общий коэффициент уменьшения 16.
Применяя только первые три из этих ограничений к приведенному примеру, размер массива аккумуляторов уменьшается почти в 1000 раз, доводя его до размера, который с гораздо большей вероятностью поместится в память современного компьютера.
Эффективный алгоритм обнаружения эллипса
[ редактировать ]Юнхун Се и Цян Цзи предлагают эффективный способ реализации преобразования Хафа для обнаружения эллипсов, преодолевая проблемы с памятью. [ 18 ] Как обсуждалось в алгоритме (на странице 2 статьи), этот подход использует только одномерный аккумулятор (для малой оси) для обнаружения эллипсов на изображении. Сложность O(N 3 ) по количеству ненулевых точек на изображении.
Ограничения
[ редактировать ]Преобразование Хафа эффективно только в том случае, если большое количество голосов попадает в правую ячейку, так что ячейку можно легко обнаружить на фоне фонового шума. Это означает, что корзина не должна быть слишком маленькой, иначе часть голосов попадет в соседние корзины, что уменьшит видимость основной корзины. [ 19 ]
Кроме того, когда количество параметров велико (то есть когда мы используем преобразование Хафа, как правило, с более чем тремя параметрами), среднее количество голосов, поданных в одном интервале, очень мало, и эти интервалы соответствуют реальной цифре. на изображении не обязательно имеют гораздо большее количество голосов, чем их соседи. Сложность возрастает со скоростью с каждым дополнительным параметром, где это размер пространства изображения и это количество параметров. (Шапиро и Стокман, 310). Таким образом, преобразование Хафа следует использовать с большой осторожностью, чтобы обнаружить что-либо, кроме линий или кругов.
Наконец, большая часть эффективности преобразования Хафа зависит от качества входных данных: края должны быть хорошо обнаружены, чтобы преобразование Хафа было эффективным. Использование преобразования Хафа на зашумленных изображениях — очень деликатный вопрос, и обычно перед этим необходимо использовать этап шумоподавления. В случае, когда изображение искажено спеклами, как в случае с радиолокационными изображениями, преобразование Радона иногда предпочтительнее для обнаружения линий, поскольку оно ослабляет шум за счет суммирования.
См. также
[ редактировать ]- Обобщенное преобразование Хафа
- Рандомизированное преобразование Хафа
- Преобразование радона
- Преобразование Фурье
Ссылки
[ редактировать ]- ^ Шапиро, Линда и Стокман, Джордж. «Компьютерное зрение», Prentice-Hall, Inc., 2001 г.
- ^ Романенго, Кьяра; Фальчидиено, Бьянка; Биазотти, Сильвия (1 сентября 2024 г.). «Расширение преобразования Хафа для распознавания и аппроксимации пространственных кривых в 3D-моделях» . Компьютерное геометрическое проектирование . 113 : 102377. doi : 10.1016/j.cagd.2024.102377 . ISSN 0167-8396 .
- ^ Дуда, Р.О. и П.Е. Харт, «Использование преобразования Хафа для обнаружения линий и кривых на изображениях», Comm. АКМ, Том. 15 , стр. 11–15 (январь 1972 г.)
- ^ Хаф, Метод ПВХ и средства для распознавания сложных узоров, патент США 3069654, 18 декабря 1962 г.
- ^ ПВХ Хаф, Машинный анализ изображений пузырьковой камеры , Proc. Межд. Конф. Ускорители высоких энергий и приборы, 1959 г.
- ^ Ричард О. Дуда ; Питер Э. Харт (апрель 1971 г.). «Использование преобразования Хафа для обнаружения линий и кривых на изображениях» (PDF) . Центр искусственного интеллекта .
- ^ Краткое введение в преобразования Радона и Хафа и их взаимосвязь . CiteSeerX.
- ^ Стивенс, Р.С. (1990). «Вероятностный подход к преобразованию Хафа» . Материалы Британской конференции по машинному зрению, 1990 г. Британская ассоциация машинного зрения: 12.1–12.6. дои : 10.5244/c.4.12 .
- ^ Дженсен, Йеппе. «Преобразование Хафа для прямых линий» (PDF) . Архивировано из оригинала (PDF) 26 апреля 2012 года . Проверено 16 декабря 2011 г.
- ^ Фернандес, Лас-Вегас; Оливейра, ММ (2008). «Обнаружение линии в реальном времени с помощью улучшенной схемы голосования с преобразованием Хафа». Распознавание образов . 41 (1): 299–314. Бибкод : 2008PatRe..41..299F . дои : 10.1016/j.patcog.2007.04.003 . S2CID 5996185 .
- ^ Лимбергер, Ф.А.; Оливейра, MM (2015). «Обнаружение плоских областей в неорганизованных облаках точек в реальном времени» (PDF) . Распознавание образов . 48 (6): 2043–2053. Бибкод : 2015PatRe..48.2043L . дои : 10.1016/j.patcog.2014.12.020 . hdl : 10183/97001 .
- ^ Фернандес, Лас-Вегас; Оливейра, ММ (2012). «Общая основа обнаружения подпространства в неупорядоченных многомерных данных». Распознавание образов . 45 (9): 3566–3579. Бибкод : 2012PatRe..45.3566F . дои : 10.1016/j.patcog.2012.02.033 .
- ^ Баллард, Д.Х. (1981). «Обобщение преобразования Хафа для обнаружения произвольных форм». Распознавание образов . 13 (2): 111–122. Бибкод : 1981PatRe..13..111B . дои : 10.1016/0031-3203(81)90009-1 . hdl : 1802/13802 .
- ^ Воссельман, Г., Дейкман, С.: « Реконструкция 3D-модели здания по облакам точек и планам местности », Международные архивы фотограмметрии, дистанционного зондирования и пространственных информационных наук, том 34, часть 3/W4, 22–24 октября 2001 г. , Аннаполис, Массачусетс, США, стр. 37–44.
- ^ Тахир Раббани: «Автоматическая реконструкция промышленных объектов - использование облаков точек и изображений». Архивировано 1 декабря 2008 г. в Wayback Machine , страницы 43–44, Публикации по геодезии 62, Делфт, 2006 г. ISBN 978-90-6132-297-9 .
- ^ Ахтерт, Эльке; Бём, Кристиан; Дэвид, Йорн; Крегер, Пер; Зимек, Артур (2008). «Глобальная корреляционная кластеризация на основе преобразования Хафа». Статистический анализ и интеллектуальный анализ данных . 1 (3): 111–127. CiteSeerX 10.1.1.716.6006 . дои : 10.1002/sam.10012 . S2CID 5111283 .
- ^ Тахир Раббани и Франк ван ден Хеувел, « Эффективное преобразование Хафа для автоматического обнаружения цилиндров в облаках точек » в материалах 11-й ежегодной конференции Высшей школы вычислений и обработки изображений (ASCI '05), Нидерланды, июнь 2005 г.
- ^ Юнхун Се; Цян Цзи (2002). «Новый эффективный метод обнаружения эллипса». Распознавание объектов, поддерживаемое взаимодействием с пользователем для сервисных роботов . Том. 2. С. 957–960. CiteSeerX 10.1.1.1.8792 . дои : 10.1109/ICPR.2002.1048464 . ISBN 978-0-7695-1695-0 . S2CID 9276255 .
- ^ «Преобразование изображения — преобразование Хафа» . Homepages.inf.ed.ac.uk . Проверено 17 августа 2009 г.
Внешние ссылки
[ редактировать ]- hough_transform.cpp — код C++ — пример библиотеки CImg ( с открытым исходным кодом библиотека , исходный код C++ , изображения в оттенках серого )
- Интерактивная демонстрация основ преобразования Хафа
- https://web.archive.org/web/20070827233423/http://www.rob.cs.tu-bs.de/content/04-teaching/06-interactive/Hough.html – Java-апплет + источник для обучения преобразование Хафа в форме пересечения наклона
- https://web.archive.org/web/20070827191440/http://www.rob.cs.tu-bs.de/content/04-teaching/06-interactive/HNF.html — Java-апплет + источник для обучения Преобразование Хафа в нормальной форме
- http://www.sydlogan.com/deskew.html. Архивировано 9 февраля 2010 г. на Wayback Machine — устранение перекосов изображений с использованием преобразования Хафа ( изображения в оттенках серого , C++ ). исходный код
- https://web.archive.org/web/20070922090216/http://imaging.gmse.net/articledeskew.html – устранение перекосов изображений с использованием преобразования Хафа ( исходный код Visual Basic )
- http://www.mitov.com/products/visionlab – Delphi , C++ и .NET, содержащая компоненты преобразования Хафа «Линия», «Окружность» и «Отрезок линии». бесплатная библиотека для образовательных целей
- Тарша-Курди Ф., Ландес Т., Груссенмейер П., 2007а. Алгоритмы преобразования Хафа и расширенные алгоритмы RANSAC для автоматического обнаружения трехмерных плоскостей крыш зданий по данным лидара. Материалы ISPRS. Мастер-класс Лазерное сканирование. Эспоо, Финляндия, 12–14 сентября 2007 г.
- Into содержит реализации линейного и кругового преобразования Хафа с открытым исходным кодом на C++.
- http://www.vision.ime.usp.br/~edelgado/defesa/code/hough.html Архивировано по адресу archive.today Преобразование Хафа для обнаружения эллипсов, реализованное на C. 5 декабря 2012 г.
- scikit-image Преобразование Хафа для линии, круга и эллипса, реализованное на Python .
- [1] Преобразование Хафа, основанное на вейвлет-фильтрации, для обнаружения круга определенного радиуса. ( Код Matlab .)
- Преобразование Хафа для линий с использованием MATLAB. Архивировано 13 апреля 2014 г. на Wayback Machine.
- Преобразование Хафа для кругов в MATLAB
- KHT — исходный код C++.
- 3DKHT — исходный код и наборы данных C++.
- Прямая линия Преобразование Хафа в Python