Мгновенный центр вращения

Мгновенный центр вращения (также известный как мгновенный центр скорости , ^[1] мгновенный центр , или полюс плоского смещения ) тела, совершающего плоское движение, — это точка, имеющая нулевую скорость в конкретный момент времени. В этот момент векторы скорости других точек тела создают круговое поле вокруг этого центра вращения , идентичное тому, что создается чистым вращением .

Плоское движение тела часто описывается с помощью плоской фигуры, движущейся в двухмерной плоскости . Мгновенный центр — это точка движущейся плоскости, вокруг которой в определенный момент времени вращаются все остальные точки.

Непрерывное движение плоскости имеет мгновенный центр для каждого значения параметра времени. Это создает кривую, называемую движущимся центром . Точки неподвижной плоскости, соответствующие этим мгновенным центрам, образуют неподвижный центрод.

Обобщением этой концепции на трехмерное пространство является вращение вокруг винта. Винт имеет ось, которая представляет собой линию в трехмерном пространстве (не обязательно проходящую через начало координат), ось вращения ; винт также имеет конечный шаг (фиксированное перемещение вдоль своей оси, соответствующее вращению вокруг оси винта).

Полюс плоского смещения

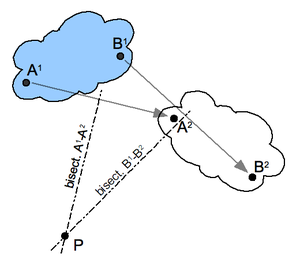
Мгновенный центр можно считать предельным случаем полюса плоского смещения.

Плоское перемещение тела из положения 1 в положение 2 определяется комбинацией плоского вращения и плоского перемещения . При любом плоском перемещении существует точка движущегося тела, которая находится в одном и том же месте до и после перемещения. Смещение можно рассматривать как вращение вокруг этого полюса.

Построение полюса плоского смещения

Сначала выберите две точки A и B в движущемся теле и найдите соответствующие точки в двух положениях; см. иллюстрацию. Постройте биссектрисы к двум отрезкам A. ¹А ² и Б ¹Б ². Пересечение P этих двух биссектрис является полюсом плоского смещения. Обратите внимание, что А ¹ и А ² лежат на окружности вокруг P. Это верно для соответствующих положений каждой точки тела.

Если два положения тела при плоском движении разделены моментом времени, то полюс смещения становится мгновенным центром. В этом случае отрезки, построенные между мгновенными положениями точек A и B, становятся векторами скорости V _A и V _B . Линии, перпендикулярные этим векторам скорости, пересекаются в мгновенном центре.

Алгебраическая конструкция декартовых координат $\left(P_{x},P_{y}\right)$ можно расположить следующим образом: Средняя точка между $A^{1}$ и $A^{2}$ имеет декартовы координаты

A_{x}^{m}={\frac {1}{2}}\left(A_{x}^{1}+A_{x}^{2}\right);\quad A_{y}^{m}={\frac {1}{2}}\left(A_{y}^{1}+A_{y}^{2}\right),

и середина между $B^{1}$ и $B^{2}$ имеет декартовы координаты

B_{x}^{m}={\frac {1}{2}}\left(B_{x}^{1}+B_{x}^{2}\right);\quad B_{y}^{m}={\frac {1}{2}}\left(B_{y}^{1}+B_{y}^{2}\right).

Два ракурса из $A^{1}$ к $A^{2}$ и из $B^{1}$ к $B^{2}$ измеренные против часовой стрелки относительно горизонтали, определяются по формуле

\tan \tau _{A}={\frac {A_{y}^{2}-A_{y}^{1}}{A_{x}^{2}-A_{x}^{1}}},\quad \tan \tau _{B}={\frac {B_{y}^{2}-B_{y}^{1}}{B_{x}^{2}-B_{x}^{1}}}

Найдите положение $P\left(P_{x},P_{y}\right)$

Method 1:

Взяв правильные ветви касательной . Пусть центр $\left(P_{x},P_{y}\right)$ вращения имеют расстояния $d_{A}$ и $d_{B}$ к двум средним точкам. Предполагая вращение по часовой стрелке (в противном случае поменяйте знак $\pi /2$ ):

{\begin{aligned}P_{x}&=A_{x}^{m}+d_{A}\cos \left(\tau _{A}-{\frac {\pi }{2}}\right)\\&=B_{x}^{m}+d_{B}\cos \left(\tau _{B}-{\frac {\pi }{2}}\right);\\P_{y}&=A_{y}^{m}+d_{A}\sin \left(\tau _{A}-{\frac {\pi }{2}}\right)\\&=B_{y}^{m}+d_{B}\sin \left(\tau _{B}-{\frac {\pi }{2}}\right).\end{aligned}}

Перепишите это как неоднородную систему линейных уравнений размера 4 × 4 с четырьмя неизвестными (два расстояния $d$ и две координаты $P$ центра):
${\begin{pmatrix}1&0&-\sin \tau _{A}&0\\1&0&0&-\sin \tau _{B}\\0&1&\cos \tau _{A}&0\\0&1&0&\cos \tau _{B}\end{pmatrix}}{\begin{pmatrix}P_{x}\\P_{y}\\d_{A}\\d_{B}\end{pmatrix}}={\begin{pmatrix}A_{x}^{m}\\B_{x}^{m}\\A_{y}^{m}\\B_{y}^{m}\end{pmatrix}}.$

Координаты центра вращения — это первые две компоненты вектора решения.

${\begin{pmatrix}P_{x}\\P_{y}\\d_{A}\\d_{B}\end{pmatrix}}={\frac {1}{\sin \left(\tau _{A}-\tau _{B}\right)}}{\begin{pmatrix}\left(B_{y}^{m}-A_{y}^{m}\right)\sin \tau _{A}\sin \tau _{B}+B_{x}^{m}\sin \tau _{A}\cos \tau _{B}-A_{x}^{m}\cos \tau _{A}\sin \tau _{B}\\\left(A_{x}^{m}-B_{x}^{m}\right)\cos \tau _{A}\cos \tau _{B}+A_{y}^{m}\sin \tau _{A}\cos \tau _{B}-B_{y}^{m}\cos \tau _{A}\sin \tau _{B}\\\left(B_{x}^{m}-A_{x}^{m}\right)\cos \tau _{B}+\left(B_{y}^{m}-A_{y}^{m}\right)\sin \tau _{B}\\\left(B_{x}^{m}-A_{x}^{m}\right)\cos \tau _{A}+\left(B_{y}^{m}-A_{y}^{m}\right)\sin \tau _{A}\\\end{pmatrix}}.$

Method 2:

Найти уравнения биссектрис двух отрезков A ¹А ² и Б ¹Б ² следующее
Уравнение прямой в виде точечно-наклонной линии имеет вид: $y-y_{0}=m(x-x_{0})$ где $(x_{0},y_{0})$ в этом суть и $m$ это наклон.
Уравнение биссектрисы A ¹А ² является $y-A_{y}^{m}=\tan \tau _{A}\left(x-A_{x}^{m}\right)$
Уравнение биссектрисы B ¹Б ² является $y-B_{y}^{m}=\tan \tau _{B}\left(x-B_{x}^{m}\right)$
Эти две биссектрисы пересекаются в точке $P\left(P_{x},P_{y}\right)$ систему из двух уравнений с двумя неизвестными и коэффициентами поэтому можно записать
${\begin{cases}P_{y}-A_{y}^{m}=\tan \tau _{A}\left(P_{x}-A_{x}^{m}\right)\\P_{y}-B_{y}^{m}=\tan \tau _{B}\left(P_{x}-B_{x}^{m}\right)\end{cases}}$
Решение этой системы
$P_{x}={\frac {B_{y}^{m}-A_{y}^{m}+A_{x}^{m}\tan \tau _{A}-B_{x}^{m}\tan \tau _{B}}{\tan \tau _{A}-\tan \tau _{B}}},\qquad P_{y}={\frac {B_{y}^{m}-A_{y}^{m}+\tan \tau _{A}\left(A_{x}^{m}-B_{x}^{m}\right)}{\tan \tau _{A}-\tan \tau _{B}}}+B_{y}^{m}$

Чистый перевод

Если перемещение между двумя положениями представляет собой чистый перенос, то биссектрисы отрезков A ¹Б ¹ и А ²Б ² образуют параллельные линии. Считается, что эти линии пересекаются в точке на бесконечной линии , поэтому говорят, что полюс этого плоского смещения «лежат в бесконечности» в направлении биссектрис.

В пределе чистое перемещение становится плоскостным движением с параллельными векторами скорости точек. В этом случае говорят, что мгновенный центр лежит на бесконечности в направлении, перпендикулярном векторам скорости.

Мгновенный центр колеса, катящегося без проскальзывания.

Рассмотрим плоское движение кругового колеса, катящегося без проскальзывания по линейной дороге; см. эскиз 3. Колесо вращается вокруг своей оси М, которая перемещается в направлении, параллельном дороге. Точка контакта P колеса с дорогой не проскальзывает, а значит, точка P имеет нулевую скорость относительно дороги. Таким образом, в тот момент, когда точка Р на колесе соприкасается с дорогой, она мгновенно становится центром.

Набор точек движущегося колеса, которые мгновенно становятся центрами, представляет собой сам круг, определяющий движущийся центр. Точки на фиксированной плоскости, соответствующие этим мгновенным центрам, представляют собой линию дороги, определяющую фиксированный центр.

Вектор скорости точки А в колесе перпендикулярен отрезку АР и пропорционален длине этого отрезка. В частности, скорости точек колеса определяются угловой скоростью колеса при вращении вокруг P. Векторы скорости ряда точек показаны на рисунке 3 и могут быть рассчитаны по следующему уравнению:

{\vec {v}}={\vec {\omega }}\times {\vec {r}}_{A}

где ${\vec {v}}$ – скорость точки А, ${\vec {\omega }}$ угловая скорость колеса и ${\vec {r}}_{A}$ вектор из точки Р в А.

Чем дальше точка колеса находится от мгновенного центра P, тем пропорционально больше ее скорость. Следовательно, точка наверху колеса движется в том же направлении, что и центр М колеса, но в два раза быстрее, так как она находится на удвоенном расстоянии от Р. Все точки, находящиеся на расстоянии, равном радиусу колеса, колесо 'r' из точки P движется с той же скоростью, что и точка M, но в разных направлениях. Это показано для точки на колесе, которая имеет ту же скорость, что и M, но движется в направлении, касательно окружности вокруг P.

Относительный центр вращения двух соприкасающихся плоских тел

Эскиз 4: Пример относительного центра вращения. Два тела, соприкасающиеся в точке C , одно вращается вокруг A , а другое вокруг B, должны иметь относительный центр вращения где-то вдоль линии AB . относительный центр вращения также должен располагаться вдоль нормали к контакту и через точку C. Поскольку части не могут проникать друг в друга , Единственное возможное решение — если относительный центр находится в D. точке

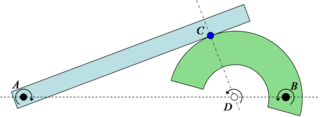
Если два плоских твердых тела находятся в контакте и каждое тело имеет свой собственный центр вращения, то относительный центр вращения между телами должен лежать где-то на линии, соединяющей два центра. В результате, поскольку чистое качение может существовать только тогда, когда центр вращения находится в точке контакта (как показано выше с колесом на дороге), это происходит только тогда, когда точка контакта проходит через линию, соединяющую два центра вращения. что может быть достигнуто чистое качение. это известно В конструкции эвольвентных передач как точка шага, при которой между шестернями нет относительного скольжения. Фактически, передаточное число между двумя вращающимися частями определяется соотношением двух расстояний к относительному центру. В примере на эскизе 4 передаточное число равно $\gamma ={\frac {AD}{BD}}$

Мгновенный центр вращения и механизмы

На рисунке 1 выше показано четырехзвенное соединение , на котором показано несколько мгновенных центров вращения. Твердое тело, обозначенное буквами ВАС, соединено звеньями Р ₁ -А и Р ₂ -В с основанием или рамой.

Тремя движущимися частями этого механизма (основание неподвижно) являются: звено P1 _- A, звено P2 _- B и корпус BAC. Для каждой из этих трех частей можно определить мгновенный центр вращения.

Учитывая первое звено P ₁ -A: все точки этого звена, включая точку A, вращаются вокруг точки P ₁ . Поскольку P ₁ — единственная точка, не движущаяся в данной плоскости, ее можно назвать мгновенным центром вращения этого звена. Точка А, находящаяся на расстоянии Р ₁ -А от Р ₁ , движется круговым движением в направлении, перпендикулярном звену Р ₁ -А, как указано вектором V _А .

То же самое относится и к звену P ₂ -B: точка P ₂ а точка B движется в направлении, указанном вектором V _B. является мгновенным центром вращения этого звена ,

Для определения мгновенного центра вращения третьего элемента тяги, корпуса ВАС, используются две точки А и В, поскольку известны его характеристики перемещения, полученные из информации о звеньях Р ₁ -А и Р ₂ -. Б.

Направление скорости точки A обозначается вектором V _A . Его мгновенный центр вращения должен быть перпендикулярен этому вектору (поскольку V _A расположен по касательной на окружности). Единственная линия, которая удовлетворяет этому требованию, — это линия, коллинеарная звену P ₁ -A. Где-то на этой линии находится точка Р — мгновенный центр вращения тела ВАС.

То, что применимо к точке A, применимо и к точке B, поэтому этот мгновенный центр вращения P расположен на линии, перпендикулярной вектору V _B , линии, коллинеарной звену P ₂ -B. Следовательно, мгновенный центр вращения P тела BAC является точкой пересечения линий, проходящих через P ₁ -A и P ₂ -B.

Поскольку этот мгновенный центр вращения P является центром всех точек тела BAC для любой случайной точки, скажем, точки C, можно определить скорость и направление движения: соединить P с C. Направление движения точки C перпендикулярно к этому соединению. Скорость пропорциональна расстоянию до точки Р.

Продолжая этот подход с двумя звеньями P ₁ -A и P ₂ -B, вращающимися вокруг своих собственных мгновенных центров вращения, можно определить центрод для мгновенного центра вращения P. Отсюда можно определить путь движения C или любой другой точки тела BAC.

Примеры применения

При биомеханическом исследовании мгновенный центр вращения наблюдается при функционировании суставов верхних и нижних конечностей. ^[2] Например, при колена анализе ^[3]^[4]^[5] лодыжка , ^[6] или плечевых суставов. ^[7]^[8] Такие знания помогают в разработке искусственных суставов и протезов , например локтевого. ^[9] или суставы пальцев. ^[10]

Исследование суставов лошадей: «...векторы скорости, определенные по мгновенным центрам вращения, показали, что суставные поверхности скользят друг по другу». ^[11]

Исследования по повороту судна, движущегося по воде. ^[12]

Улучшить тормозные . характеристики автомобиля можно путем изменения конструкции механизма педали тормоза ^[13]

Проектирование подвески велосипеда, ^[14] или автомобиля. ^[15]

В случае соединительного звена в четырехзвенной рычажной системе , такой как подвеска на двойных поперечных рычагах (вид спереди), перпендикуляры к скорости лежат вдоль звеньев, соединяющих заземленное звено с соединительным звеном. Данная конструкция используется для установления кинематического центра крена подвески.

См. также

Ссылки

^ Иллюстрированный словарь машиностроения: английский, немецкий, французский, голландский, русский (Springer Science & Business Media, 17 апреля 2013 г. - 422 страницы)
^ «Физиология мышц — момент руки сустава» .
^ Описание и измерение движения коленного сустава . ^{[ постоянная мертвая ссылка ]}
^ Мурхед JD, Монтгомери SC, Харви DM (сентябрь 2003 г.). «Мгновенная оценка центра вращения с использованием метода Рело и метода боковой экстраполяции». Дж Биомеханик . 36 (9): 1301–7. дои : 10.1016/S0021-9290(03)00156-8 . ПМИД 12893038 .
^ Холлман Дж. Х., Дойсингер Р. Х., Ван Диллен Л. Р., Матава М. Дж. (август 2003 г.). «Гендерные различия в кинематике качения и скольжения колена». Клин Ортоп Релат Рес . 413 (413): 208–21. дои : 10.1097/01.blo.0000072902.36018.fe . ПМИД 12897612 . S2CID 45191914 .
^ Маганарис CN, Бальзопулос В., Сержант А.Дж. (август 1998 г.). «Изменения момента плеча ахиллова сухожилия от покоя до максимального изометрического подошвенного сгибания: наблюдения in vivo у человека» . Журнал физиологии . 510 (Часть 3): 977–85. дои : 10.1111/j.1469-7793.1998.977bj.x . ПМК 2231068 . ПМИД 9660906 . Архивировано из оригинала 8 сентября 2012 г.
^ Биомеханика плеча.
^ Поппен Н.К., Уокер П.С. (март 1976 г.). «Нормальные и ненормальные движения плеча». J Bone Joint Surg Am . 58 (2): 195–201. дои : 10.2106/00004623-197658020-00006 . ПМИД 1254624 .
^ US 5030237 Протез локтя.
^ «Имплантат пироуглеродного сустава пальца» (PDF) . Архивировано из оригинала (PDF) 21 июля 2011 г. Проверено 22 августа 2008 г.
^ Колахан П., Пиотровски Г., Пулос П. (сентябрь 1988 г.). «Кинематический анализ мгновенных центров вращения пястно-фалангового сустава лошади». Am J Vet Res . 49 (9): 1560–5. ПМИД 3223666 .
^ «ЧАСТЬ VI Навигация и маневрирование судов» (PDF) . Архивировано из оригинала (PDF) 15 декабря 2009 г. Проверено 22 августа 2008 г.
^ GB 1443270 Опоры педали тормоза с регулируемым механическим передаточным числом — General Motors, 1976 г.
^ US 7100930 Система задней подвески велосипеда .
^ Реза Н. Джазар (2008). Динамика транспортного средства: теория и применение . Берлин: Шпрингер. ISBN 978-0-387-74243-4 .

[1] Иллюстрированный словарь машиностроения: английский, немецкий, французский, голландский, русский (Springer Science & Business Media, 17 апреля 2013 г. - 422 страницы)

[2] «Физиология мышц — момент руки сустава» .

[3] Описание и измерение движения коленного сустава . ^{[ постоянная мертвая ссылка ]}

[4] Мурхед JD, Монтгомери SC, Харви DM (сентябрь 2003 г.). «Мгновенная оценка центра вращения с использованием метода Рело и метода боковой экстраполяции». Дж Биомеханик . 36 (9): 1301–7. дои : 10.1016/S0021-9290(03)00156-8 . ПМИД 12893038 .

[5] Холлман Дж. Х., Дойсингер Р. Х., Ван Диллен Л. Р., Матава М. Дж. (август 2003 г.). «Гендерные различия в кинематике качения и скольжения колена». Клин Ортоп Релат Рес . 413 (413): 208–21. дои : 10.1097/01.blo.0000072902.36018.fe . ПМИД 12897612 . S2CID 45191914 .

[6] Маганарис CN, Бальзопулос В., Сержант А.Дж. (август 1998 г.). «Изменения момента плеча ахиллова сухожилия от покоя до максимального изометрического подошвенного сгибания: наблюдения in vivo у человека» . Журнал физиологии . 510 (Часть 3): 977–85. дои : 10.1111/j.1469-7793.1998.977bj.x . ПМК 2231068 . ПМИД 9660906 . Архивировано из оригинала 8 сентября 2012 г.

[7] Биомеханика плеча.

[8] Поппен Н.К., Уокер П.С. (март 1976 г.). «Нормальные и ненормальные движения плеча». J Bone Joint Surg Am . 58 (2): 195–201. дои : 10.2106/00004623-197658020-00006 . ПМИД 1254624 .

[9] US 5030237 Протез локтя.

[10] «Имплантат пироуглеродного сустава пальца» (PDF) . Архивировано из оригинала (PDF) 21 июля 2011 г. Проверено 22 августа 2008 г.

[11] Колахан П., Пиотровски Г., Пулос П. (сентябрь 1988 г.). «Кинематический анализ мгновенных центров вращения пястно-фалангового сустава лошади». Am J Vet Res . 49 (9): 1560–5. ПМИД 3223666 .

[12] «ЧАСТЬ VI Навигация и маневрирование судов» (PDF) . Архивировано из оригинала (PDF) 15 декабря 2009 г. Проверено 22 августа 2008 г.

[13] GB 1443270 Опоры педали тормоза с регулируемым механическим передаточным числом — General Motors, 1976 г.

[14] US 7100930 Система задней подвески велосипеда .

[15] Реза Н. Джазар (2008). Динамика транспортного средства: теория и применение . Берлин: Шпрингер. ISBN 978-0-387-74243-4 .

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]