Ось зоны

Зонно-осевые структуры нанокристаллов (слева) (справа)

Ось зоны , термин, который иногда используется для обозначения «высокосимметричных» ориентаций в кристалле, чаще всего относится к любому направлению, относящемуся к прямой решетке (в отличие от обратной решетки ) кристалла в трех измерениях. Поэтому он индексируется прямыми индексами решетки, а не индексами Миллера .

Оси зон высокой симметрии через кристаллическую решетку, в частности, часто лежат в направлении туннелей сквозь кристалл между плоскостями атомов. Это связано с тем, что, как мы увидим ниже, такие направления осей зон обычно лежат в пределах более чем одной плоскости атомов в кристалле.

Индексация оси зоны

Основная статья: Индекс Миллера

Трансляционная инвариантность кристаллической решетки описывается набором элементарных ячеек , прямыми базисными векторами решетки ( контравариантными или полярные ), называемые a , b и c , или, что то же самое, параметрами решетки , то есть величинами векторов, называемых a , b и c , и углами между ними, называемыми α (между b и c ), β (между c и a ) и γ (между a и b ). Векторы прямой решетки имеют компоненты, измеряемые в единицах расстояния, таких как метры (м) или ангстремы (Å).

Вектор решетки индексируется по его координатам в системе прямого базиса решетки. $\{{\bf {a}},{\bf {b}},{\bf {c}}\}$ и обычно помещается в квадратные скобки []. Таким образом, прямой вектор решетки ${\bf {s}}_{uvw}$, или $[uvw]$, определяется как $u{\bf {a}}+v{\bf {b}}+w{\bf {c}}$. Угловые скобки ⟨⟩ используются для обозначения симметрично эквивалентного класса векторов решетки (т. е. набора векторов, группы симметрии порожденных действием ) решетки . в случае кубической решетки Например, ⟨100⟩ представляет собой [100], [010], [001], [ 1 00], [0 1 0] и [00 1 ], поскольку каждый из этих векторов симметрично эквивалентен. при повороте вокруг оси на 90 градусов. Полоса над координатой соответствует отрицательному знаку (например, $[{\overline {1}}00]=-{\bf {a}}$).

Термин «ось зоны» более конкретно относится к направлению вектора решетки в прямом пространстве. Например, поскольку векторы решетки [120] и [240] параллельны, их ориентация обе соответствуют зоне ⟨120⟩ кристалла. Подобно тому, как набор плоскостей решетки в прямом пространстве соответствует вектору обратной решетки в дополнительном пространстве пространственных частот и импульсов, определяется «зона». как набор плоскостей обратной решетки в частотном пространстве , который соответствует вектору решетки в прямом пространстве.

Обратное пространство, аналог оси зоны, представляет собой « нормаль к плоскости решетки » или «направление g-вектора». Векторы обратной решетки ( одна форма или осевое ) индексируются по Миллеру с использованием координат в базисе обратной решетки. $\{{\bf {a}}^{*},{\bf {b}}^{*},{\bf {c}}^{*}\}$ вместо этого обычно между круглыми скобками () (аналогично квадратным скобкам [] для прямых векторов решетки). Фигурные скобки {} (не путать с математическим набором ) используются для обозначения симметрично эквивалентного класса векторов обратной решетки, аналогично угловым скобкам ⟨⟩ для классов прямых векторов решетки.

Здесь, ${\bf {a}}^{*}\equiv (b\times c)/V_{c}$, ${\bf {b}}^{*}\equiv (c\times a)/V_{c}$, и ${\bf {c}}^{*}\equiv (a\times b)/V_{c}$, где объем элементарной ячейки $V_{c}={\bf {a}}\cdot ({\bf {b}}\times {\bf {c}})$ ( $\cdot$ обозначает скалярное произведение и $\times$ перекрестное произведение ). Таким образом, вектор обратной решетки ${\bf {g}}_{hkl}$ или $(hkl)=h{\bf {a}}^{*}+k{\bf {b}}^{*}+l{\bf {c}}^{*}$ имеет направление, перпендикулярное кристаллографической плоскости, и величину $g_{hkl}=1/d_{hkl}$ равен обратной величине расстояния $d_{hkl}$ между этими $(hkl)$ плоскости, измеряемые в единицах пространственной частоты, например, циклов на ангстрем (циклы/Å).

Соглашения о скобках для индексов Миллера прямой и обратной решетки в кристаллографии

Объект	Класс эквивалентности	Конкретный вектор	Единицы	Трансформация
зона или решетка-вектор s uvw	$\langle {uvw\rangle }\,$	$[uvw]\,$	прямое пространство, например, [метры]	контравариантный или полярный
плоскость или g-вектор g hkl	$\{hkl\}\,$	$(hkl)\,$	обратное пространство, например [циклов/м]	ковариантный или осевой

Полезное и довольно общее правило кристаллографических « двойных векторных пространств в 3D», например, обратной решетки, заключается в том, что условие перпендикулярности вектора прямой решетки [ uvw ] (или оси зоны) к вектору обратной решетки ( hkl ) может быть записано со скалярным произведением как $[uvw]\cdot (hkl)=uh+vk+wl=0$. Это верно, даже если, как это часто бывает, набор базисных векторов, используемый для описания решетки, не является декартовым .

Шаблоны зональной оси

[ uvw ] В более широком смысле, диаграмма оси зоны (ZAP) представляет собой картину дифракции , полученную с падающим лучом, например, электронов , рентгеновских лучей или нейтронов, движущихся вдоль направления решетки, заданного индексами оси зоны [ uvw ]. Из-за малой длины волны λ электроны высокой энергии, используемые в электронных микроскопах, имеют очень большой радиус сферы Эвальда (1/λ), так что дифракция электронов обычно «освещает» дифракционные пятна с g-векторами ( hkl ), перпендикулярными [ увв ].

с алмазной гранью, кремния Кубический кластер атомов вид вниз по зоне [011] (слева), с соответствующим рисунком оси зоны (справа).

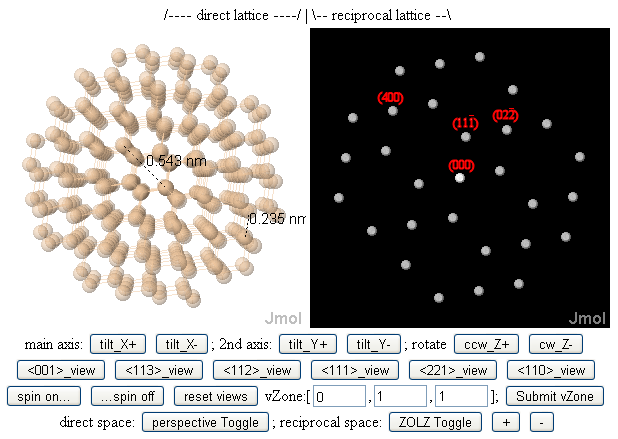
Одним из результатов этого, как показано на рисунке выше, является то, что зоны с «низким индексом» обычно перпендикулярны плоскостям решетки с «низким индексом Миллера », которые, в свою очередь, имеют малые пространственные частоты (значения g) и, следовательно, большую периодичность решетки. (d-расстояния). Возможная интуиция, лежащая в основе этого, заключается в том, что в электронной микроскопии электронные лучи должны быть направлены вниз по широким (т.е. легко видимым) туннелям между столбцами атомов в кристалле, направляя луч вниз в зону с низким индексом (и, следовательно, с высокой симметрией). ось может помочь.

См. также

• Кристаллография
• Двойной базис
• Обратная решетка
• Индекс Миллера
• Дифракция
• Электронная дифракция
• Просвечивающая электронная микроскопия

Внешние ссылки

• Международные таблицы по кристаллографии