Сотовая модель
Эта статья требует внимания эксперта в области биологии . Конкретная проблема заключается в следующем: большие объемы технического материала здесь не помещены в контекст. ( март 2022 г. ) |

Клеточная модель — это математическая модель аспектов биологической клетки , предназначенная для исследований in silico .
Разработка таких моделей была задачей системной биологии и математической биологии . Он предполагает разработку эффективных алгоритмов , структур данных , средств визуализации и связи для организации интеграции больших объемов биологических данных с целью компьютерного моделирования . Он предполагает использование компьютерного моделирования клеточных , которые подсистем, таких как сети метаболитов и ферментов включают метаболизм , передачи сигналов пути и сети регуляции генов .
Обзор [ править ]
Цикл эукариотических клеток очень сложен и является одной из наиболее изученных тем, поскольку его неправильная регуляция приводит к раку .Возможно, это хороший пример математической модели, поскольку она имеет дело с простыми вычислениями, но дает достоверные результаты. Две исследовательские группы [1] [2] создали несколько моделей клеточного цикла, имитирующих несколько организмов. Недавно они создали общую модель эукариотического клеточного цикла, которая может представлять конкретного эукариота в зависимости от значений параметров, демонстрируя, что особенности отдельных клеточных циклов обусловлены различными концентрациями и сродством белков, в то время как основные механизмы сохраняются (Csikasz -Надь и др., 2006).
Эти модели с помощью системы обыкновенных дифференциальных уравнений показывают изменение во времени ( динамическая система ) белка внутри одной типичной клетки; этот тип модели называется детерминированным процессом (тогда как модель, описывающая статистическое распределение концентраций белка в популяции клеток, называется стохастическим процессом ).
Чтобы получить эти уравнения, необходимо выполнить итерационный ряд шагов: сначала несколько моделей и наблюдений объединяются для формирования согласованной диаграммы, и выбираются соответствующие кинетические законы для записи дифференциальных уравнений, таких как кинетика скорости стехиометрических реакций, Михаэлис-Ментен. кинетика ферментативно-субстратных реакций и кинетика Гольдбетера-Кошланда для сверхчувствительных факторов транскрипции, после чего параметры уравнений (константы скорости, коэффициенты эффективности ферментов и константы Михаэлиса) должны быть подобраны для соответствия наблюдениям; когда их невозможно установить, кинетическое уравнение пересматривается, а когда это невозможно, изменяется схема подключения. Параметры подбираются и проверяются с использованием наблюдений как за диким типом, так и за мутантами, такие как период полураспада белка и размер клеток.
Для подбора параметров необходимо изучить дифференциальные уравнения. Это можно сделать либо путем моделирования, либо путем анализа.
В моделировании, учитывая стартовый вектор (список значений переменных), развитие системы рассчитывается путем решения уравнений на каждом временном интервале с небольшими приращениями.
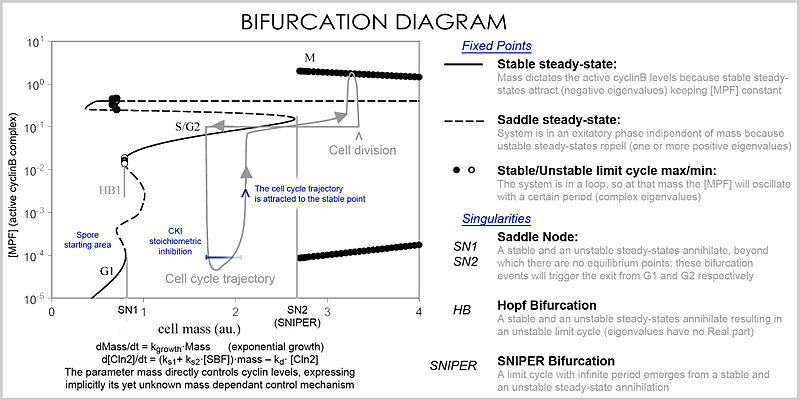
При анализе свойства уравнений используются для исследования поведения системы в зависимости от значений параметров и переменных. Систему дифференциальных уравнений можно представить в виде векторного поля , где каждый вектор описывает изменение (концентрации двух и более белков), определяющее, куда и с какой скоростью движется траектория (моделирование). Векторные поля могут иметь несколько особых точек: стабильная точка , называемая стоком, которая притягивает во всех направлениях (заставляя концентрации достигать определенного значения), нестабильная точка , либо источник, либо седловая точка, которая отталкивается (заставляя концентрации достигать определенного значения). изменяться от определенного значения) и предельный цикл, замкнутая траектория, к которой по спирали приближаются несколько траекторий (заставляя концентрации колебаться).
Лучшее представление, которое может обрабатывать большое количество переменных и параметров, называется бифуркационной диаграммой ( теорией бифуркаций ): наличие этих особых точек устойчивого состояния при определенных значениях параметра (например, массы) представляется точкой, и как только параметр достигает определенного значения, происходит качественное изменение, называемое бифуркацией, при котором меняется природа пространства, что имеет глубокие последствия для концентрации белка: клеточный цикл имеет фазы (частично соответствующие G1 и G2), в которых масса, через стабильная точка, контролирует уровни циклина и фазы (фазы S и M), в которых концентрации изменяются независимо, но как только фаза изменилась в момент бифуркации ( контрольная точка клеточного цикла ), система не может вернуться к предыдущим уровням, поскольку при текущая масса векторного поля совершенно другая, и массу нельзя повернуть обратно через событие бифуркации, что делает контрольную точку необратимой. В частности, контрольные точки S и M регулируются посредством специальных бифуркаций, называемых Бифуркация Хопфа и бифуркация бесконечного периода .
уровня Моделирование молекулярного
Коллектив ячейки [3] это программное обеспечение для моделирования, которое позволяет хранить динамические биологические данные, строить вычислительные модели, стимулировать, разбивать и воссоздавать модели. Разработку возглавляет Томас Хеликар, [4] исследователь в области компьютерной биологии. Он предназначен для биологов, студентов, изучающих вычислительную биологию, преподавателей, специализирующихся на преподавании наук о жизни, и исследователей в области наук о жизни. Сложности математики и информатики встроены в серверную часть, и можно узнать о методах, используемых для моделирования биологических видов, но сложные математические уравнения, алгоритмы, программирование не требуются и, следовательно, не будут препятствовать построению модели.
Математическая основа Cell Collective основана на общей методике качественного (дискретного) моделирования, в которой механизм регулирования каждого узла описывается логической функцией [более полную информацию о логическом моделировании см. [5] [6] ].
В июльском номере журнала Cell за 2012 год команда под руководством Маркуса Коверта из Стэнфорда опубликовала наиболее полную на сегодняшний день вычислительную модель клетки. Модель Mycoplasmagentium , состоящая примерно из 500 генов , содержит 28 алгоритмически независимых компонентов, включающих работу из более чем 900 источников. Он учитывает взаимодействие полного генома , транскриптома , протеома и метаболома организма, что означает значительный прогресс в этой области. [7] [8]
Большинство попыток моделирования процессов клеточного цикла были сосредоточены на широких и сложных молекулярных взаимодействиях множества различных химических веществ, включая несколько молекул циклина и циклин-зависимой киназы, поскольку они соответствуют фазам S , M , G1 и G2 клеточного цикла . В опубликованной в 2014 году статье в журнале PLOS по вычислительной биологии сотрудники Оксфордского университета , Технологического института Вирджинии и Института генетики и развития Ренна создали упрощенную модель клеточного цикла, используя только одно взаимодействие циклин/CDK. Эта модель продемонстрировала способность контролировать полностью функциональное деление клеток посредством регуляции и манипулирования только одним взаимодействием и даже позволила исследователям пропускать фазы путем изменения концентрации CDK. [9] Эта модель может помочь понять, как относительно простые взаимодействия одного химического вещества переходят в модель деления клеток на клеточном уровне.
Проекты [ править ]
В стадии реализации находится несколько проектов. [10]
- CytoSolve — коммерческая платформа, возможно с использованием MATLAB.
- Synthecell - Экспериментальная группа
- Кариот - Университет Индианы - больше не действует
- Проект E-Cell – последнее обновление: 2020 г.
- Виртуальная ячейка - Центр здоровья Университета Коннектикута - Платформа моделирования, а не создание проекта ячейки
- Кремниевый элемент - больше не активен
- WholeCell – Стэнфордский университет – больше не активен
- MCell - Национальный центр многомасштабного моделирования биологических систем (MMBioS) - Действует с 2023 г.
См. также [ править ]
- Визуализация биологических данных
- Биологические приложения теории бифуркаций
- Программное обеспечение для молекулярного моделирования
- Мембранные вычисления — это задача моделирования именно клеточной мембраны .
- Биохимические переключения в клеточном цикле
- Масару Томита
Ссылки [ править ]
- ^ «Лаборатория Джей Джей Тайсона» . Вирджинский технологический институт . Проверено 20 июля 2011 г.
- ^ «Группа исследования динамики молекулярных сетей» . Будапештский университет технологии и экономики . Архивировано из оригинала 30 октября 2019 г. Проверено 20 июля 2011 г.
- ^ «Интерактивное моделирование биологических сетей» .
- ^ «Хеликар Лаборатория - Члены» . Архивировано из оригинала 19 октября 2019 г. Проверено 15 февраля 2016 г.
- ^ Моррис М.К., Саес-Родригес Дж., Зоргер П.К., Лауффенбургер Д.А.. Логические модели для анализа сотовых сигнальных сетей. Биохимия (2010) 49(15):3216–24.10.1021/bi902202q.
- ^ Хеликар Т., Коваль Б., Мадрахимов А., Шреста М., Педерсен Дж., Лимбу К. и др. Bio-Logic Builder: нетехнический инструмент для построения динамических качественных моделей. PLoS One (2012) 7(10):e46417.10.1371/journal.pone.0046417
- ^ http://covertlab.stanford.edu/publicationpdfs/mgenitalium_whole_cell_2012_07_20.pdf [ постоянная мертвая ссылка ]
- ^ «Исследователи Стэнфорда создали первую полную компьютерную модель организма» . 19 июля 2012 г.
- ^ Жерар, Клод; Тайсон, Джон Дж.; Кудрез, Дэмиен; Новак, Бела (06 февраля 2015 г.). «Управление клеточным циклом с помощью минимальной сети Cdk» . ПЛОС Компьютерная Биол . 11 (2): e1004056. Бибкод : 2015PLSCB..11E4056G . дои : 10.1371/journal.pcbi.1004056 . ПМЦ 4319789 . ПМИД 25658582 .
- ^ Гершон, Дайан (2002). «Кремниевые мечты в биологической лаборатории» . Природа . 417 (6892): 4–5. Бибкод : 2002Natur.417....4G . дои : 10.1038/nj6892-04a . ПМИД 12087360 . S2CID 10737442 .