Призматическое соединение антипризм

Соединение n p / q -угольных антипризм
п = 2 5/3-угольный 5/2-угольный
Тип	Однородный состав
Индекс	q нечетный: UC 23 q даже: UC 25
Многогранники	n p / q -угольные антипризмы
Символы Шлефли (n=2)	ß{2,2p/кв} ßr{2,p/q}
Диаграммы Кокстера (n=2)
Лица	2 n { p / q } (если p / q = 2), 2 np треугольника
Края	4 нп
Вершины	2 нп
Группа симметрии	nq нечетный: np -кратный антипризматический ( D np d ) nq четный: np -кратно призматический ( D np h )
Подгруппа, ограничивающаяся одним компонентом	q нечетный: p -кратный антипризматический ( D p d ) q четный: p -кратно призматический ( D p h )

В геометрии призматическое соединение антипризмы — это категория соединения однородного многогранника . Каждый член этого бесконечного семейства однородных многогранников представляет собой симметричное расположение антипризм, имеющих общую ось вращательной симметрии.

Бесконечная семья

Это бесконечное семейство можно перечислить следующим образом:

• Для каждого натурального числа n ≥1 и для каждого рационального числа p / q >3/2 (выраженного через p и q взаимно простые числа ) возникает соединение n p / q -угольных антипризм с группой симметрии:
  • D _{np d,} если nq нечетно
  • D _{np h,} если nq четное

Где p / q =2, компонентом является тетраэдр (или диадическая антипризма). В этом случае, если n то соединение представляет собой звезду-октангулу с более высокой симметрией ( OH _{= 2 ,} ).

Соединения двух антипризм

Соединения двух n -антипризм делят свои вершины с 2 n - призмой и существуют как два чередующихся набора вершин.

Декартовы координаты вершин антипризмы с n -угольными основаниями и равнобедренными треугольниками:

• $\left(\cos {\frac {k\pi }{n}},\sin {\frac {k\pi }{n}},(-1)^{k}h\right)$
• $\left(\cos {\frac {k\pi }{n}},\sin {\frac {k\pi }{n}},(-1)^{k+1}h\right)$

с k в диапазоне от 0 до 2 n -1; если треугольники равносторонние,

$2h^{2}=\cos {\frac {\pi }{n}}-\cos {\frac {2\pi }{n}}.$

Соединения 2-х антипризм

2- угольный антипризма (тетраэдры)	2 треугольных антипризма (октаэдры)	2 квадрата антипризма	2 шестиугольных антипризма	2 пентаграммы пересек антипризма

Соединение двух трапецоэдров (двойников)

Двойниками призматического соединения антипризм являются соединения трапецоэдров :

Два кубика (треугольные трапецииэдры)

Соединение трёх антипризм

Для соединений трех двуугольных антипризм они повернуты на 60 градусов, а три треугольных антипризмы повернуты на 40 градусов.

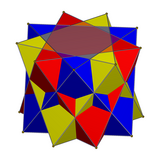Три тетраэдра	Три октаэдра

Ссылки

• Скиллинг, Джон (1976), «Однородные соединения однородных многогранников», Mathematical Proceedings of the Cambridge Philosophical Society , 79 (3): 447–457, doi : 10.1017/S0305004100052440 , MR   0397554 .