Конечные выводы фильтра изображения
| Линейный аналог электронные фильтры |
|---|
Фильтры, разработанные с использованием методологии импеданса изображения , страдают специфическим недостатком теории. Прогнозируемые характеристики фильтра рассчитываются в предположении, что фильтр оканчивается собственными импедансами изображения на каждом конце. Обычно это не так; фильтр будет оснащен фиксированными сопротивлениями. Это приводит к отклонению отклика фильтра от теоретического. В этой статье объясняется, как можно принять во внимание влияние концевых окончаний фильтра изображений.
Как правило, эффект оконечных нагрузок заключается в том, что они вызывают округление частотной характеристики при границе среза. Метод изображения предсказывает резкий скачок наклона характеристики при отсечке, что на практике не реализуется, хотя хорошо спроектированный фильтр изображения может приблизиться к этому. Еще одним предсказанием метода изображения является нулевая потеря в полосе пропускания (при условии идеальных компонентов без потерь). Опять же, на практике этого достичь невозможно, поскольку отражения от конечных выводов всегда вызывают некоторые потери.
- Части этой статьи или раздела основаны на знаниях читателя о комплексного импеданса представлении конденсаторов и катушек индуктивности , а также на знании в частотной области представления сигналов .
Символы, используемые в этой статье
[ редактировать ]Импедансы
[ редактировать ]- на импеданс изображения конце 1
- импеданс изображения на конце 2
- импеданс изображения, когда оба конца идентичны
- согласующее сопротивление на конце 1
- согласующее сопротивление на конце 2
- оконечное сопротивление, когда оба конца идентичны
Коэффициенты
[ редактировать ]- коэффициент отражения на конце 1
- коэффициент отражения на конце 2
- коэффициент отражения, когда оба конца одинаковы
- коэффициент передачи на конце 1
- коэффициент передачи на конце 2
- комплексный коэффициент распространения фильтра
- коэффициент ослабления фильтра
- фазовый коэффициент фильтра
Обратите внимание, что все эти коэффициенты определяются относительно импеданса изображения, а не фактического входного сопротивления фильтра.
Общий случай
[ редактировать ]
Передаточная функция любого фильтра, подключенного, как показано на схеме выше, определяется выражением
где
Обратите внимание, что V i — это номинальное напряжение, которое вырабатывалось бы генератором, если бы он был согласован с его характеристическим сопротивлением (т. е. R 1 ), а не фактическое напряжение, появляющееся на входных клеммах фильтра.
Далее можно отметить, что первая часть выражения,
- ,
совпадает с выражением для передаточной функции без учета концевых окончаний. Таким образом, вторая часть выражения — это часть отклика, вызванная несовпадением импедансов;
Симметричный случай
[ редактировать ]Если фильтр имеет симметричные импедансы и окончания изображения, выражение может быть значительно уменьшено. Обратите внимание, что не требуется, чтобы фильтр был симметричным внутри, а только чтобы конечные секции имели одинаковый импеданс изображения, обращенный к идентичным оконечным импедансам.
Дальнейшее упрощение может быть сделано, если в фильтре нет резистивных потерь (или предполагается, что они пренебрежимо малы). этом случае импеданс изображения является чисто действительным ( RI В ) в полосе пропускания и чисто мнимым ( iXI ) в полосе задерживания. Величина передаточной функции определяется выражением
где полоса пропускания,
и для полосы задерживания,
Антиметрический корпус
[ редактировать ]Аналогичное упрощение можно сделать для антиметрических фильтров без потерь. В этом случае замена
превращается в общее уравнение. Для полосы пропускания
и для полосы задерживания,
Антиметрический в этом контексте означает, что импедансы и нагрузки изображения фильтра на каждом конце двойственны друг другу. Это будет в том случае, если фильтр имеет на каждом конце последовательную и шунтирующую секции одного и того же типа соответственно. Симметричные фильтры имеют четное количество полусекций, а антиметрические — нечетное количество полусекций. В подавляющем большинстве случаев конструкция фильтра будет либо симметричной, либо антиметрической, и будет применяться одно из этих сокращенных выражений.
Некоторые примеры графиков ответа
[ редактировать ]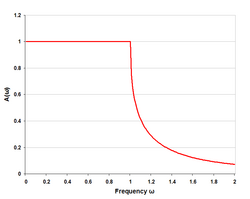 |
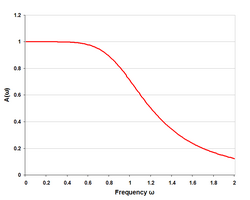 |
 |
См. также
[ редактировать ]- Импеданс изображения
- Составной фильтр изображения
- Двойной импеданс
- Фильтр прототипов
- Категория: Фильтры импеданса изображения
Ссылки
[ редактировать ]- Маттеи, Янг, Джонс. Микроволновые фильтры, схемы согласования импедансов и структуры связи , стр. 68–72, McGraw-Hill, 1964.














![{\displaystyle A(i\omega)={\frac {V_{o}}{V_{i}}}={\sqrt {\frac {Z_{I2}}{Z_{I1}}}}e^{ -\gamma }\left[{\frac {\tau _{I1}\tau _{I2}}{1-e^{-2\gamma }r_{I1}r_{I2}}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/76e9302e29805bb2b4de91543363bec086456af8)





![{\displaystyle \left[{\frac {\tau _{I1}\tau _{I2}}{1-e^{-2\gamma }r_{I1}r_{I2}}}\right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5eb12bcf02ede759fe0c646265e8453160f35cb1)
![{\displaystyle A(i\omega)=e^{-\gamma }\left[{\frac {4Z_{I}R}{(R+Z_{I})^{2}-e^{-2\ гамма }(R-Z_{I})^{2}}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/226a60fe1eb49709c78075721166bfb46495868c)





