Теория короля драконов

Обложка сборника статей о королях драконов

Король драконов — это двойная метафора события, которое одновременно чрезвычайно велико по размеру или эффекту («король») и имеет уникальное происхождение («дракон») по сравнению с другими событиями из той же системы. События DK генерируются или соответствуют таким механизмам, как положительная обратная связь , переломные моменты , бифуркации и фазовые переходы , которые имеют тенденцию возникать в нелинейных и сложных системах и служат для усиления событий Короля Драконов до экстремальных уровней. Понимая и отслеживая эту динамику, можно добиться некоторой предсказуемости таких событий.

Теория короля драконов была разработана Дидье Сорнеттом , который выдвинул гипотезу о том, что многие кризисы на самом деле являются ДК, а не черными лебедями , т.е. они могут быть в некоторой степени предсказуемы. Учитывая важность кризисов для долгосрочной организации множества систем, теория ДК призывает уделять особое внимание изучению и мониторингу крайностей, а также принимать динамический подход. С научной точки зрения такие крайности интересны, потому что они могут выявить скрытые, часто скрытые, организующие принципы. С практической точки зрения, следует изучать экстремальные риски, но не забывать, что значительная неопределенность будет присутствовать почти всегда и ее следует тщательно учитывать при принятии решений относительно управления рисками и проектирования.

Теория Короля Дракона связана с такими концепциями, как теория черного лебедя, выбросы , сложные системы , нелинейная динамика , степенные законы , теория экстремальных значений , прогнозирование , экстремальные риски и управление рисками .

Черные лебеди и короли драконов

можно Чёрного лебедя рассматривать как метафору события, которое удивляет (для наблюдателя), имеет большой эффект и, после наблюдения, рационализируется задним числом. Теория черных лебедей является эпистемологической , связанной с ограниченностью знаний и понимания наблюдателя. Этот термин был введен и популяризирован Нассимом Талебом и ассоциировался с такими понятиями, как тяжелые хвосты , нелинейные выплаты, ошибка модели и даже неопределенность Найта , чья терминология «непознаваемых неизвестных» событий была популяризирована бывшим министром обороны США Дональдом. Рамсфельд. Талеб утверждает, что события «черного лебедя» непредсказуемы, и на практике эта теория побуждает человека «готовиться, а не предсказывать» и ограничивать подверженность экстремальным колебаниям.

Концепция «черного лебедя» важна и представляет собой обоснованную критику людей, фирм и обществ, которые безответственны в том смысле, что они чрезмерно уверены в своей способности предвидеть риск и управлять им. Однако утверждение о том, что экстремальные события в целом непредсказуемы, может также привести к отсутствию подотчетности в сфере управления рисками. Фактически известно, что в широком диапазоне физических систем экстремальные события в той или иной степени предсказуемы. Просто необходимо иметь достаточно глубокое понимание структуры и динамики фокальной системы и умение ее контролировать. Это владения королей драконов. Такие события Талеб назвал «серыми лебедями». Более строгое различие между черными лебедями, серыми лебедями и королями драконов затруднено, поскольку черные лебеди не имеют точного определения в физических и математических терминах. Однако техническая разработка концепций книги Черный лебедь» « подробно описана в документе «Тихий риск». Анализ точного определения черного лебедя в контексте управления рисками был написан профессором Терье Авеном.

За пределами степенных законов

5000 крупнейших просадок для 8 различных фьючерсных контрактов, построенных в соответствии с их эмпирическими значениями CCDF , сдвинутыми в 10 раз для наглядности. Пунктирные линии соответствуют степенному закону.

Общеизвестно, что многие явления как в естественных, так и в социальных науках имеют степенную статистику ( распределение Парето ). Кроме того, из теории экстремальных значений известно, что широкий диапазон распределений (класс Фреше) имеет хвосты, которые являются асимптотически степенными. В результате при возникновении кризисов и экстремальных ситуаций хвосты степенного закона являются «нормальным» случаем. Уникальным свойством степенных законов является то, что они масштабно-инвариантны , самоподобны и фрактальны . Это свойство подразумевает, что все события — как большие, так и малые — генерируются одним и тем же механизмом, и, следовательно, не будет отдельных предшественников, с помощью которых можно было бы предсказать самые крупные события. Известная концептуальная основа событий такого типа — самоорганизованная критичность . Подобные концепции совместимы с теорией черного лебедя. Однако Талеб также заявил, что рассмотрение степенного закона в качестве модели вместо модели с более светлыми хвостами (например, гауссовой ) «превращает черных лебедей в серых» в том смысле, что модель степенного закона дает непренебрежимо малую вероятность большим события.

В различных исследованиях было обнаружено, что, несмотря на то, что степенной закон хорошо моделирует хвост эмпирического распределения, самые крупные события существенно отстают (т. е. намного больше, чем можно было бы ожидать в рамках модели). Такие события интерпретируются как короли драконов, поскольку они указывают на отход от общего процесса, лежащего в основе степенного закона. Примеры этого включают крупнейшие выбросы радиации, происходящие в результате аварий на атомных электростанциях, крупнейший город (агломерацию) в выборке городов страны, крупнейшие крахи на финансовых рынках и внутридневные оптовые цены на электроэнергию.

Механизмы

Складчатая бифуркация в экологии

С физической точки зрения короли драконов могут быть связаны со сменой режима, бифуркациями и переломными моментами сложных неравновесных систем. Например, катастрофу ( складчатую бифуркацию ) глобальной экологии, проиллюстрированную на рисунке, можно было бы считать королем драконов: многие наблюдатели были бы удивлены такой резкой сменой состояния. Однако хорошо известно, что в динамических системах существует множество предвестников по мере приближения системы к катастрофе.

Положительная обратная связь также является механизмом, который может порождать королей драконов. Например, во время давки количество бегущего скота увеличивает уровень паники, что приводит к бегству большего количества скота и так далее. В человеческой динамике такое стадное и массовое поведение также наблюдалось в толпе, на фондовых рынках и т. д. (см. Стадное поведение ).

Слева: Иллюстрация траектории системы в районе возникновения пузырька. Справа: эмпирический PDF-файл (гистограмма) высот пиков траекторий в двойном логарифмическом масштабе.

Короли драконов также возникают из-за пузырьков аттрактора в связанных осцилляционных системах. Пузырение аттрактора - это типичное поведение, возникающее в сетях связанных осцилляторов, где система обычно вращается в инвариантном многообразии с хаотичным аттрактором (где пиковые траектории низкие), но периодически выталкивается (из-за шума) в область, где орбиты локально отталкиваются. из инвариантного многообразия (где пиковые траектории велики). Эти экскурсии формируют королей драконов, как показано на рисунке. Утверждается, что такие модели могут описывать многие реальные явления, такие как землетрясения, активность мозга и т. д. Механическая модель блока и пружины, рассматриваемая как модель геологических разломов и их динамики землетрясений, дала аналогичное распределение.

Также возможно, что короли драконов создаются в результате контроля или вмешательства системы. То есть попытка подавить выброс стресса или смерть в динамических сложных системах может привести к накоплению стресса или созреванию в сторону нестабильности. Например, кустарниковые / лесные пожары являются естественным явлением во многих районах. Такие пожары неудобны, и поэтому мы можем желать, чтобы их старательно тушили. Это приводит к длительным периодам отсутствия неудобных пожаров, однако и при отсутствии пожаров накапливается валежная древесина. Как только это накопление достигает критической точки и начинается пожар, огонь становится настолько большим, что его невозможно контролировать — уникальное событие, которое можно считать королем драконов. Другие меры, такие как бездействие (позволяющее возникать небольшим пожарам естественным образом) или стратегически контролируемое горение , позволяют избежать огромных пожаров, допуская частые небольшие пожары. Другой пример – денежно-кредитная политика . Программы количественного смягчения и низкие процентные ставки политика является обычным явлением и направлена ​​на предотвращение рецессий, содействие экономическому росту и т. д. Однако такие программы создают нестабильность, увеличивая неравенство в доходах, поддерживая слабые фирмы и раздувая пузыри активов. В конечном итоге такая политика, направленная на сглаживание экономических колебаний, приведет к огромной коррекции – королю драконов.

Короли драконов как статистические выбросы

Схема функции плотности вероятности, где режим короля драконов представлен куском массы глубоко в хвосте.

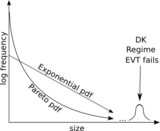
Короли драконов являются особями по определению. Однако при вызове выбросов DK есть важное условие: в стандартной статистике выбросы обычно являются ошибочными значениями и отбрасываются, либо выбираются статистические методы, которые каким-то образом нечувствительны к выбросам. Напротив, ДК представляют собой выбросы, которые очень информативны и должны быть в центре внимания статистов. Таким образом, первым шагом является выявление ДК в исторических данных. Существующие тесты основаны либо на асимптотических свойствах эмпирической функции распределения (ЭФР), либо на асимптотических свойствах эмпирической функции распределения (ЭФР). или на предположении о базовой кумулятивной функции распределения (CDF) данных.

Оказывается, тестирование выбросов относительно экспоненциального распределения носит очень общий характер. Последнее следует из теоремы Пикандса – Балкемы – де Хаана о теории экстремальных значений , которая утверждает, что широкий диапазон распределений асимптотически (выше высоких порогов) имеет хвосты экспоненциального или степенного закона. Кстати, это одно из объяснений того, почему хвосты степенного закона так распространены при изучении экстремумов. В завершение, поскольку натуральный логарифм хвоста степенного закона является экспоненциальным, можно взять логарифм данных степенного закона, а затем проверить наличие выбросов относительно экспоненциального хвоста. Существует множество тестовых статистических данных и методов проверки выбросов в экспоненциальной выборке. Внутренний тест последовательно проверяет самую большую точку, затем вторую по величине и так далее, пока первый тест, который не будет отклонен (т. е. нулевая гипотеза о том, что точка не является выбросом, не будет отклонена). Количество отклоненных тестов определяет количество выбросов. Например, где $x_{(1)}>x_{(2)}>\cdots >x_{(n)}$ — отсортированная выборка, внутренний устойчивый тест использует тестовую статистику $T_{r,m}=x_{(r)}/(x_{(m)}+\cdots +x_{(n)})$ где r — проверяемая точка $(r=1,2,3,\ldots )$, и $r<m<n$ где m — заранее заданное максимальное количество выбросов. На каждом шаге должно вычисляться значение p для статистики теста , и, если оно ниже некоторого уровня, тест отклоняется. Этот тест имеет много желательных свойств: он не требует указания количества выбросов, он не склонен к заниженной (маскировке) и завышенной (затоплению) оценке количества выбросов, его легко реализовать, и тест является независимым. значения параметра экспоненциального хвоста.

Примеры

(II) Эмпирический CCDF журнала выброса радиации (серый пунктир) и ущерба (черный), вызванного авариями на атомных электростанциях, сплошные линии обозначают хвост подобранного степенного закона. (III) Эмпирический CCDF населения в городских агломерациях внутри страны, масштабированный так, чтобы второй по величине имел размер 1. Выбросы помечены.

Некоторые примеры того, когда короли драконов были обнаружены как выбросы, включают:

• финансовые крахи, измеряемые просадками , где выбросы соответствуют террористическим атакам (например, взрыву в Лондоне в 2005 году ) и внезапному краху 2010 года ;
• выбросы радиации и финансовые потери, вызванные авариями на атомных электростанциях, где выбросы соответствуют неконтролируемым катастрофам, когда механизмы безопасности вышли из строя;
• крупнейший город (измеряется по численности населения в его агломерации) среди населения городов внутри страны, где крупнейший город играет непропорционально важную роль в динамике страны и извлекает выгоду из уникального роста;
• внутридневные оптовые цены на электроэнергию; и
• трехволновое нелинейное взаимодействие — можно подавить появление королей драконов.

Моделирование и прогнозирование

Предсказуемость, основанная на взаимодействии и разнообразии в системе

То, как моделировать и предсказывать королей драконов, зависит от основного механизма. Однако общий подход потребует постоянного мониторинга фокальной системы и сравнения измерений с ( нелинейной или сложной ) динамической моделью. Было высказано предположение, что чем более однородна система и чем сильнее ее взаимодействия, тем более предсказуемой она будет.

Моделирование и прогноз пузыря (суперэкспоненциального роста) с помощью логопериодического степенного закона

Например, в нелинейных системах с фазовыми переходами в критической точке хорошо известно, что в окрестности критической точки возникает окно предсказуемости из-за предвестников: система медленнее восстанавливается после возмущений, автокорреляционных изменений, дисперсии увеличивается, увеличивается пространственная связность и т. д. Эти свойства использовались для прогнозирования во многих приложениях, начиная от изменений в биосфере и заканчивая изменениями в биосфере. к разрыву гидробаков на ракете «Ариан». Применение к широкому кругу явлений стимулировало взгляд на сложные системы, который представляет собой трансдисциплинарный подход и не зависит от понимания первопринципов.

Четыре режима просмотров в день видеороликов YouTube.

Для явлений неустойчивого роста (например, численности населения или цен на акции) можно рассмотреть модель роста, характеризующуюся конечной временной сингулярностью, которая является критической точкой изменения режима роста. В системах, инвариантных по дискретному масштабу, такой моделью является степенной закон роста, дополненный логпериодической функцией. Подгонка этой модели к данным роста ( нелинейная регрессия ) позволяет предсказать сингулярность, то есть конец неустойчивого роста. Это применялось ко многим проблемам, например: разрыв материалов, землетрясения, рост и лопание пузырей на финансовых рынках

Интересной динамикой, которую следует учитывать, которая может выявить развитие успеха блокбастера, являются эпидемические явления : например, распространение чумы, вирусные явления в средствах массовой информации, распространение паники и волатильности на фондовых рынках и т. д. В таком случае Эффективный подход состоит в том, чтобы разложить активность/колебания на экзогенную и эндогенную части и изучить эндогенную динамику, которая может привести к весьма влиятельным всплескам активности.

Прогнозирование и принятие решений

Учитывая модель и данные, можно получить оценку статистической модели. Эту модельную оценку затем можно использовать для вычисления интересных величин, таких как условная вероятность возникновения события короля драконов в будущем интервале времени и наиболее вероятное время возникновения. При статистическом моделировании экстремальных значений и использовании сложных или нелинейных динамических моделей неизбежно возникает значительная неопределенность. Таким образом, следует тщательно подходить к количественной оценке неопределенности: учитывать не только случайность, присутствующую в подобранной стохастической модели, но и неопределенность ее оцененных параметров (например, с помощью байесовских методов или путем сначала моделирования параметров, а затем моделирования на основе модели с этими параметрами). ) и неопределенность при выборе модели (например, при рассмотрении ансамбля различных моделей).

Затем можно использовать оцененные вероятности и связанные с ними неопределенности для принятия решений. В простейшем случае выполняется бинарная классификация : предсказание появления короля драконов в будущем интервале, если вероятность его появления достаточно высока и с достаточной уверенностью. Например, можно предпринять определенное действие, если предсказано появление короля драконов. Оптимальное решение затем сбалансирует стоимость ложных срабатываний / ложных срабатываний и промахов / ложных тревог в соответствии с заданной функцией потерь . Например, если цена промаха очень велика по сравнению с ценой ложной тревоги, оптимальным решением будет обнаружение королей драконов чаще, чем они происходят. Следует также изучить истинную положительную скорость предсказания. Чем меньше это значение, тем слабее тест и тем ближе он к территории черного лебедя. На практике выбор оптимального решения и вычисление его свойств должны осуществляться путем перекрестной проверки с историческими данными (если они доступны) или смоделированными данными (если вы знаете, как моделировать королей драконов).

В динамической обстановке набор данных со временем будет расти, а оценка модели и ее предполагаемые вероятности будут меняться. Затем можно рассмотреть возможность объединения последовательности оценок/вероятностей при выполнении прогнозирования. В такой динамической обстановке тест, скорее всего, будет слабым большую часть времени (например, когда система находится в равновесии), но по мере приближения к королю драконов и появления предшественников уровень истинного положительного результата должен увеличиваться.

Важность экстремальных рисков

Короли драконов формируют особые виды событий, ведущие к чрезвычайным рискам (которые также могут быть возможностями). Крайние риски важны и должны быть самоочевидны. Стихийные бедствия дают множество примеров (например, падение астероидов, приведшее к вымиранию). Некоторые статистические примеры воздействия крайностей таковы: крупнейшая авария на атомной электростанции ( Чернобыльская катастрофа ) имела примерно такой же ущерб (измеренный в расчетной стоимости в долларах США), как и все (+- 175) другие исторические ядерные аварии вместе взятые; на долю крупнейших 10 процентов утечек частных данных организаций приходится 99 процентов от общего количества украденной частной информации, пять крупнейших эпидемий с 1900 года унесли в 20 раз больше смертей, чем остальные 1363, и т. д. В целом такая статистика поступает при наличии распределений с тяжелыми хвостами , а присутствие королей драконов усилит и без того чрезмерный эффект экстремальных событий.

Несмотря на важность экстремальных событий, из-за невежества, несогласованных стимулов и когнитивных предубеждений их часто не удается адекватно предвидеть. С технической точки зрения, это приводит к плохо определенным моделям, в которых распределения не имеют достаточно тяжелых хвостов и недооценивают как последовательную, так и многомерную зависимость экстремальных событий. Некоторые примеры таких неудач в оценке риска включают использование моделей Гаусса в финансах ( Блэка-Шоулза , гауссова копула, LTCM ), использование гауссовских процессов и теории линейных волн, неспособных предсказать возникновение волн-убийц , провал экономических модели в целом для прогнозирования финансового кризиса 2007–2008 годов , а также недооценка внешних событий, каскадов и нелинейных эффектов при вероятностной оценке рисков , что привело к непредвидению ядерной катастрофы на Фукусиме-дайити в 2011 году. Такие влиятельные неудачи подчеркивают важность изучения крайностей.

Управление рисками

Концепция короля драконов поднимает множество вопросов о том, как можно справиться с риском. Конечно, по возможности следует избегать больших рисков (часто называемых «подходом черного лебедя»). Однако во многих случаях подверженность риску является необходимостью, и необходимо найти компромисс между риском и доходностью.

В адаптивной системе, где предсказание королей драконов оказывается успешным, можно действовать, чтобы защитить систему или даже получить прибыль. Как спроектировать такие устойчивые системы , а также их системы мониторинга рисков в режиме реального времени? — это важная и междисциплинарная проблема, в которой необходимо учитывать королей драконов.

С другой стороны, когда дело доходит до количественной оценки риска в конкретной системе (будь то банк, страховая компания, дамба, мост или социально-экономическая система), риск необходимо учитывать в течение определенного периода. , например, ежегодно. Обычно интересуют такие статистические данные, как годовая вероятность потерь или ущерба, превышающих определенную стоимость ( стоимость под угрозой ), другие меры хвостового риска и периоды повторяемости . Чтобы дать такую ​​характеристику риска, динамические короли драконов должны быть рассмотрены с точки зрения ежегодной статистики частоты и серьезности. Эти статистические данные о частоте и серьезности можно затем объединить в такой модели, как сложный процесс Пуассона .

При условии, что статистические свойства системы постоянны во времени (стационарны), статистика частоты и серьезности может быть построена на основе прошлых наблюдений, моделирования и/или предположений. Если нет, то можно только строить сценарии. Однако в любом случае, учитывая существующую неопределенность, следует рассмотреть ряд сценариев. Из-за нехватки данных об экстремальных событиях, принципа экономности и теоретических результатов теории экстремальных значений об универсальных моделях хвоста обычно полагаются на модель хвоста обобщенного распределения Парето (GPD). Однако такая модель исключает ДК. достаточные основания полагать, что Короли-Драконы присутствуют, или если кто-то просто хочет рассмотреть сценарий, можно, например, рассмотреть смесь плотностей ГПД Таким образом, когда у кого-то есть и плотности для режима ДК.