Алгебра Брауэра

В математике алгебра Брауэра — это ассоциативная алгебра, введенная Рихардом Брауэром. ^[1] в контексте теории представлений ортогональной группы . Она играет ту же роль, которую симметрическая группа играет для теории представлений полной линейной группы в двойственности Шура – Вейля .

Структура [ править ]

Алгебра Брауэра ${\mathfrak {B}}_{n}(\delta )$ это $\mathbb {Z} [\delta ]$ -алгебра в зависимости от выбора натурального числа $n$ . Здесь $\delta$ является неопределенным, но на практике $\delta$ часто специализируется на измерении фундаментального представления ортогональной группы. $O(\delta )$ . Алгебра Брауэра имеет размерность

\dim {\mathfrak {B}}_{n}(\delta )={\frac {(2n)!}{2^{n}n!}}=(2n-1)!!=(2n-1)(2n-3)\cdots 5\cdot 3\cdot 1

Схематическое определение [ править ]

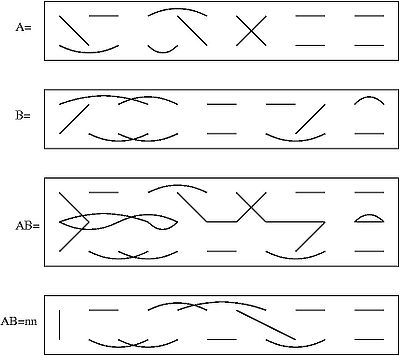
Основа ${\mathfrak {B}}_{n}(\delta )$ состоит из всех пар из множества $2n$ элементы $X_{1},...,X_{n},Y_{1},...,Y_{n}$ (то есть все совершенные паросочетания полного графа $K_{n}$ : любые два из $2n$ элементы могут сопоставляться друг с другом независимо от их символов). Элементы $X_{i}$ обычно пишутся подряд, с элементами $Y_{i}$ под ними.

Произведение двух базисных элементов $A$ и $B$ получается путем конкатенации: сначала идентифицируются конечные точки в нижнем ряду $A$ и верхний ряд $B$ (Рисунок AB на диаграмме), затем удалив конечные точки в средней строке и соединив конечные точки в оставшихся двух строках, если они соединены напрямую или по пути в AB (Рисунок AB=nn на диаграмме). все замкнутые петли в середине АВ Тем самым удаляются . Продукт $A\cdot B$ базовых элементов затем определяется как базовый элемент, соответствующий новой паре, умноженный на $\delta ^{r}$ где $r$ — количество удаленных петель. В примере $A\cdot B=\delta ^{2}AB$ .

Генераторы и отношения [ править ]

${\mathfrak {B}}_{n}(\delta )$ также может быть определен как $\mathbb {Z} [\delta ]$ -алгебра с генераторами $s_{1},\ldots ,s_{n-1},e_{1},\ldots ,e_{n-1}$ удовлетворяющие следующим отношениям:

Отношения симметричной группы :

s_{i}^{2}=1

s_{i}s_{j}=s_{j}s_{i}

в любое время

|i-j|>1

s_{i}s_{i+1}s_{i}=s_{i+1}s_{i}s_{i+1}

Почти- идемпотентное соотношение:

e_{i}^{2}=\delta e_{i}

Коммутация:

e_{i}e_{j}=e_{j}e_{i}

s_{i}e_{j}=e_{j}s_{i}

в любое время

|i-j|>1

Запутывание отношений

e_{i}e_{i\pm 1}e_{i}=e_{i}

s_{i}s_{i\pm 1}e_{i}=e_{i\pm 1}e_{i}

e_{i}s_{i\pm 1}s_{i}=e_{i}e_{i\pm 1}

Раскручивание:

s_{i}e_{i}=e_{i}s_{i}=e_{i}

:

e_{i}s_{i\pm 1}e_{i}=e_{i}

В этой презентации $s_{i}$ представляет собой диаграмму, на которой $X_{k}$ всегда связан с $Y_{k}$ прямо под ним, за исключением $X_{i}$ и $X_{i+1}$ которые связаны с $Y_{i+1}$ и $Y_{i}$ соответственно. Сходным образом $e_{i}$ представляет собой диаграмму, на которой $X_{k}$ всегда связан с $Y_{k}$ прямо под ним, за исключением $X_{i}$ быть подключенным к $X_{i+1}$ и $Y_{i}$ к $Y_{i+1}$ .

Основные свойства [ править ]

Алгебра Брауэра является подалгеброй алгебры разбиения .

Алгебра Брауэра ${\mathfrak {B}}_{n}(\delta )$ является полупростым, если $\delta \in \mathbb {C} -\{0,\pm 1,\pm 2,\dots ,\pm n\}$ . ^[2]^[3]

Подалгебра ${\mathfrak {B}}_{n}(\delta )$ генерируется генераторами $s_{i}$ групповая алгебра симметрической группы $S_{n}$ .

Подалгебра ${\mathfrak {B}}_{n}(\delta )$ генерируется генераторами $e_{i}$ — алгебра Темперли-Либа $TL_{n}(\delta )$ . ^[4]

Алгебра Брауэра является клеточной алгеброй .

Для пары $A$ позволять $n(A)$ быть числом замкнутых петель, образованных путем идентификации $X_{i}$ с $Y_{i}$ для любого $i=1,2,\dots ,n$ : затем след Джонса ${\text{Tr}}(A)=\delta ^{n(A)}$ подчиняется ${\text{Tr}}(AB)={\text{Tr}}(BA)$ т.е. это действительно след .

Представления [ править ]

Модули Brauer-Specht [ править ]

Модули Брауэра-Шпехта — это конечномерные модули алгебры Брауэра. Если $\delta$ таков, что ${\mathfrak {B}}_{n}(\delta )$ является полупростым,они образуют полный набор простых модулей ${\mathfrak {B}}_{n}(\delta )$ . ^[4] Эти модули параметризуются разделами , поскольку они построены из модулей Specht симметричной группы , которые сами параметризуются разделами.

Для $0\leq \ell \leq n$ с $\ell \equiv n{\bmod {2}}$ , позволять $B_{n,\ell }$ быть множеством совершенных паросочетаний $n+\ell$ элементы $X_{1},\dots ,X_{n},Y_{1},\dots ,Y_{\ell }$ , такой, что $Y_{j}$ совпадает с одним из $n$ элементы $X_{1},\dots ,X_{n}$ . Для любого кольца $k$ , пространство $kB_{n,\ell }$ это левый ${\mathfrak {B}}_{n}(\delta )$ -модуль, в котором базовые элементы ${\mathfrak {B}}_{n}(\delta )$ действовать путем конкатенации графов. (Это действие может привести к совпадениям, нарушающим ограничение, $Y_{1},\dots ,Y_{\ell }$ не могут совпадать друг с другом: такие графы необходимо модифицировать.) Более того, пространство $kB_{n,\ell }$ это право $S_{\ell }$ -модуль. ^[5]

Учитывая модуль Specht $V_{\lambda }$ из $kS_{\ell }$ , где $\lambda$ является разделом $\ell$ (т.е. $|\lambda |=\ell$ ), соответствующий Брауэра-Шпехта модуль ${\mathfrak {B}}_{n}(\delta )$ является

W_{\lambda }=kB_{n,|\lambda |}\otimes _{kS_{|\lambda |}}V_{\lambda }\qquad {\big (}|\lambda |\leq n,|\lambda |\equiv n{\bmod {2}}{\big )}

Основой этого модуля является набор элементов $b\otimes v$ , где $b\in B_{n,|\lambda |}$ такова, что $|\lambda |$ линии, которые заканчиваются элементами $Y_{j}$ не пересекайся и $v$ принадлежит основе $V_{\lambda }$ . ^[5] Размерность

\dim(W_{\lambda })={\binom {n}{|\lambda |}}(n-|\lambda |-1)!!\dim(V_{\lambda })

т.е. произведение биномиального коэффициента , двойного факториала и размерности соответствующего модуля Шпехта, который определяется формулой длины крюка .

Двойственность Шура-Вейля [ править ]

Позволять $V=\mathbb {R} ^{d}$ быть евклидовым векторным пространством размерности $d$ , и $O(V)=O(d,\mathbb {R} )$ соответствующую ортогональную группу. Тогда напиши $B_{n}(d)$ по специализации $\mathbb {R} \otimes _{\mathbb {Z} [\delta ]}{\mathfrak {B}}_{n}(\delta )$ где $\delta$ действует на $\mathbb {R}$ путем умножения на $d$ . Тензорная мощность $V^{\otimes n}:=\underbrace {V\otimes \cdots \otimes V} _{n{\text{ times}}}$ естественно, является $B_{n}(d)$ - модуль : $s_{i}$ действует путем переключения $i$ й и $(i+1)$ тензорный фактор и $e_{i}$ действует путем сжатия с последующим расширением $i$ й и $(i+1)$ тензорный коэффициент, т.е. $e_{i}$ действует как

v_{1}\otimes \cdots \otimes v_{i-1}\otimes {\Big (}v_{i}\otimes v_{i+1}{\Big )}\otimes \cdots \otimes v_{n}\mapsto v_{1}\otimes \cdots \otimes v_{i-1}\otimes \left(\langle v_{i},v_{i+1}\rangle \sum _{k=1}^{d}(w_{k}\otimes w_{k})\right)\otimes \cdots \otimes v_{n}

где $w_{1},\ldots ,w_{d}$ любой ортонормированный базис $V$ . (Фактически сумма не зависит от выбора этого базиса.)

Это действие полезно для обобщения двойственности Шура-Вейля : если $d\geq n$ , образ $B_{n}(d)$ внутри $\operatorname {End} (V^{\otimes n})$ является централизатором $O(V)$ внутри $\operatorname {End} (V^{\otimes n})$ , и наоборот, образ $O(V)$ является централизатором $B_{n}(d)$ . ^[2] Тензорная мощность $V^{\otimes n}$ поэтому является одновременно $O(V)$ - и $B_{n}(d)$ -модуль и удовлетворяет

V^{\otimes n}=\bigoplus _{\lambda }U_{\lambda }\boxtimes W_{\lambda }

где $\lambda$ работает над подмножеством разделов, так что $|\lambda |\leq n$ и $|\lambda |\equiv n{\bmod {2}}$ , $U_{\lambda }$ является неприводимым $O(V)$ -модуль и $W_{\lambda }$ является модулем Брауэра-Шпехта $B_{n}(d)$ .

Отсюда следует, что алгебра Брауэра естественным образом действует в пространстве полиномов на $V^{n}$ , коммутирующий с действием ортогональной группы.

Если $\delta$ — отрицательное четное целое число, алгебра Брауэра связана двойственностью Шура-Вейля с симплектической группой ${\text{Sp}}_{-\delta }(\mathbb {C} )$ , а не ортогональная группа.

Алгебра Брауэра со стеной [ править ]

Алгебра Брауэра со стеной ${\mathfrak {B}}_{r,s}(\delta )$ является подалгеброй ${\mathfrak {B}}_{r+s}(\delta )$ . Схематически он состоит из диаграмм, где разрешены только пары типов $X_{i\leq r}-X_{j>r}$ , $Y_{i\leq r}-Y_{j>r}$ , $X_{i\leq r}-Y_{j\leq r}$ , $X_{i>r}-Y_{j>r}$ . Это равносильно наличию стены, которая разделяет $X_{i\leq r},Y_{i\leq r}$ от $X_{i>r},Y_{i>r}$ , и требуя этого $X-Y$ пары пересекают стену, пока $X-X,Y-Y$ пары - нет. ^[6]

Алгебра Брауэра со стенками порождается формулой $\{s_{i}\}_{1\leq i\leq r+s-1,i\neq r}\cup \{e_{r}\}$ . Эти генераторы подчиняются основным соотношениям ${\mathfrak {B}}_{r+s}(\delta )$ которые включают их, плюс два отношения ^[7]

e_{r}s_{r+1}s_{r-1}e_{r}s_{r-1}=e_{r}s_{r+1}s_{r-1}e_{r}s_{r+1}\quad ,\quad s_{r-1}e_{r}s_{r+1}s_{r-1}e_{r}=s_{r+1}e_{r}s_{r+1}s_{r-1}e_{r}

(В ${\mathfrak {B}}_{r+s}(\delta )$ , эти два соотношения следуют из основных соотношений.)

Для $\delta$ натуральное целое число, пусть $V$ — естественное представление полной линейной группы $GL_{\delta }(\mathbb {C} )$ . Алгебра Брауэра со стеной ${\mathfrak {B}}_{r,s}(\delta )$ оказывает естественное действие на $V^{\otimes r}\otimes (V^{*})^{\otimes s}$ , связанный двойственностью Шура-Вейля с действием $GL_{\delta }(\mathbb {C} )$ . ^[6]

См. также [ править ]

Алгебра Бирмана–Венцля , деформация алгебры Брауэра.

Ссылки [ править ]

^ Брауэр, Ричард (1937), «Об алгебрах, связанных с полупростыми непрерывными группами», Annals of Mathematics , вторая серия, 38 (4), Annals of Mathematics: 857–872, doi : 10.2307/1968843 , ISSN 0003-486X , JSTOR 1968843
^ Jump up to: Перейти обратно: ^а ^б Бенкарт, Джорджия; Мун, Донхо (26 апреля 2005 г.), «Тензорные представления произведений алгебр Темперли-Либа и полиномов Чебышева», «Представления алгебр и смежные темы » , Провиденс, Род-Айленд: Американское математическое общество, стр. 57–80, doi : 10.1090 /фик/045/05 , ISBN 9780821834152
^ Венцль, Ганс (1988), «О структуре централизующих алгебр Брауэра», Annals of Mathematics , Second Series, 128 (1): 173–193, doi : 10.2307/1971466 , ISSN 0003-486X , JSTOR 1971466 , MR 0951511
^ Jump up to: Перейти обратно: ^а ^б Халверсон, Том; Джейкобсон, Теодор Н. (24 августа 2018 г.). «Таблицы множеств-разделов и представления диаграммных алгебр». arXiv : 1808.08118v2 [ math.RT ].
^ Jump up to: Перейти обратно: ^а ^б Мартин, Пол П. (11 августа 2009 г.). «Матрицы разложения алгебры Брауэра над комплексным полем». arXiv : 0908.1500v1 [ math.RT ].
^ Jump up to: Перейти обратно: ^а ^б Кокс, Антон; Вишер, Де; Доти, Стивен; Мартин, Пол (6 сентября 2007 г.). «О блоках алгебры Брауэра с стенками». arXiv : 0709.0851v1 [ math.RT ].
^ Булгакова, Д.В.; Огиевецкий, О. (24 ноября 2019 г.). «Процедура слияния алгебры Брауэра со стенками». Журнал геометрии и физики . 149 : 103580. arXiv : 1911.10537v1 . doi : 10.1016/j.geomphys.2019.103580 . S2CID 208267893 .

[bra37-1] Брауэр, Ричард (1937), «Об алгебрах, связанных с полупростыми непрерывными группами», Annals of Mathematics , вторая серия, 38 (4), Annals of Mathematics: 857–872, doi : 10.2307/1968843 , ISSN 0003-486X , JSTOR 1968843

[bm05-2] Jump up to: Перейти обратно: ^а ^б Бенкарт, Джорджия; Мун, Донхо (26 апреля 2005 г.), «Тензорные представления произведений алгебр Темперли-Либа и полиномов Чебышева», «Представления алгебр и смежные темы » , Провиденс, Род-Айленд: Американское математическое общество, стр. 57–80, doi : 10.1090 /фик/045/05 , ISBN 9780821834152

[wen88-3] Венцль, Ганс (1988), «О структуре централизующих алгебр Брауэра», Annals of Mathematics , Second Series, 128 (1): 173–193, doi : 10.2307/1971466 , ISSN 0003-486X , JSTOR 1971466 , MR 0951511

[hj18-4] Jump up to: Перейти обратно: ^а ^б Халверсон, Том; Джейкобсон, Теодор Н. (24 августа 2018 г.). «Таблицы множеств-разделов и представления диаграммных алгебр». arXiv : 1808.08118v2 [ math.RT ].

[mar09-5] Jump up to: Перейти обратно: ^а ^б Мартин, Пол П. (11 августа 2009 г.). «Матрицы разложения алгебры Брауэра над комплексным полем». arXiv : 0908.1500v1 [ math.RT ].

[cvdm07-6] Jump up to: Перейти обратно: ^а ^б Кокс, Антон; Вишер, Де; Доти, Стивен; Мартин, Пол (6 сентября 2007 г.). «О блоках алгебры Брауэра с стенками». arXiv : 0709.0851v1 [ math.RT ].

[bo19-7] Булгакова, Д.В.; Огиевецкий, О. (24 ноября 2019 г.). «Процедура слияния алгебры Брауэра со стенками». Журнал геометрии и физики . 149 : 103580. arXiv : 1911.10537v1 . doi : 10.1016/j.geomphys.2019.103580 . S2CID 208267893 .

[1]

[2]

[3]

[4]

[5]

[6]

[7]