Реляционная алгебра

Не путать с Реляционной алгеброй .

В теории баз данных реляционная алгебра — это теория, которая использует алгебраические структуры для моделирования данных и определения запросов к ним с хорошо обоснованной семантикой . Теория была представлена ​​Эдгаром Ф. Коддом .

Основное применение реляционной алгебры — обеспечить теоретическую основу для реляционных баз данных , особенно языков запросов для таких баз данных, главным из которых является SQL . Реляционные базы данных хранят табличные данные, представленные в виде отношений . Запросы к реляционным базам данных часто также возвращают табличные данные, представленные в виде отношений.

Основная цель реляционной алгебры — определить операторы , которые преобразуют одно или несколько входных отношений в выходное отношение. Учитывая, что эти операторы принимают отношения в качестве входных данных и создают отношения в качестве выходных данных, их можно комбинировать и использовать для выражения сложных запросов, которые преобразуют несколько входных отношений (данные которых хранятся в базе данных) в одно выходное отношение (результаты запроса).

Унарные операторы принимают на вход одно отношение. Примеры включают операторы для фильтрации определенных атрибутов (столбцов) или кортежей (строк) из входного отношения. Бинарные операторы принимают два отношения в качестве входных данных и объединяют их в одно выходное отношение. Например, взяв все кортежи, найденные в любом отношении ( объединение ), удалив кортежи из первого отношения, найденного во втором отношении ( различие ), расширив кортежи первого отношения кортежами во втором отношении, соответствующими определенным условиям, и так далее.

Могут быть включены и другие, более продвинутые операторы, где включение или исключение определенных операторов приводит к созданию семейства алгебр.

Введение

Реляционной алгебре уделялось мало внимания за пределами чистой математики до публикации Э. Ф. Кодда в реляционной модели данных 1970 году. Кодд предложил такую ​​алгебру в качестве основы для языков запросов к базам данных. (См. раздел «Реализации» .)

Реляционная алгебра оперирует однородными наборами кортежей. $S=\{(s_{j1},s_{j2},...s_{jn})|j\in 1...m\}$ где мы обычно интерпретируем m как количество строк в таблице и n — количество столбцов. Все записи в каждом столбце иметь тот же тип. Пять примитивных операторов алгебры Кодда — это выбор , проекция , декартово произведение (также называемое векторным произведением или перекрестным соединением ), объединение множеств и разность множеств .

Операторы установки

Реляционная алгебра использует объединение множеств , разность множеств и декартово произведение из теории множеств , но добавляет к этим операторам дополнительные ограничения.

Для объединения множеств и различия множеств два задействованных отношения должны быть совместимы по объединению , то есть два отношения должны иметь одинаковый набор атрибутов. Поскольку пересечение множеств определяется в терминах объединения множеств и разности множеств, два отношения, участвующие в пересечении множеств, также должны быть совместимы по объединению.

Чтобы определить декартово произведение, два задействованных отношения должны иметь непересекающиеся заголовки, то есть у них не должно быть общего имени атрибута.

Кроме того, декартово произведение определяется иначе, чем в теории множеств , в том смысле, что кортежи считаются «поверхностными» для целей операции. То есть декартово произведение набора из n -кортежей с набором из m -кортежей дает набор «сплющенных» ( n + m ) -кортежей (тогда как базовая теория множеств предписывала бы набор из 2-х кортежей, каждый из которых содержащий n -кортеж и m -кортеж). Более формально R × S определяется следующим образом:

$$R\times S:=\{(r_{1},r_{2},\dots ,r_{n},s_{1},s_{2},\dots ,s_{m})|(r_{1},r_{2},\dots ,r_{n})\in R,(s_{1},s_{2},\dots ,s_{m})\in S\}$$

Мощность декартова произведения есть произведение мощностей его факторов, т. е. | Р × С | = | р | × | С |.

Проекция ( П )

Основная статья: Проекция (реляционная алгебра)

Проекция , — это унарная операция записанная как $\Pi _{a_{1},\ldots ,a_{n}}(R)$ где $a_{1},\ldots ,a_{n}$ представляет собой набор имен атрибутов. Результат такого проектирования определяется как набор , который получается, когда все кортежи в R ограничены набором $\{a_{1},\ldots ,a_{n}\}$.

Примечание. При реализации в стандарте SQL «проекция по умолчанию» возвращает мультимножество вместо набора, а проекция Π для устранения повторяющихся данных получается путем добавления DISTINCT ключевое слово .

Выбор ( р )

Основная статья: Выбор (реляционная алгебра)

Обобщенный выбор — это унарная операция, записываемая как $\sigma _{\varphi }(R)$ где φ — пропозициональная формула , состоящая из атомов , разрешенных при нормальном выборе , и логических операторов. $\wedge$ ( и ), $\lor$ ( или ) и $\neg$ ( отрицание ). Этот выбор выбирает все те кортежи в R, для которых выполняется φ .

Чтобы получить список всех друзей или деловых партнеров в адресной книге, выбор можно записать как $\sigma _{{\text{isFriend = true}}\,\lor \,{\text{isBusinessContact = true}}}({\text{addressBook}})$. Результатом будет отношение, содержащее каждый атрибут каждой уникальной записи, где isFriend имеет значение true или isBusinessContact имеет значение true.

Переименовать ( п )

Основная статья: Переименование (реляционная алгебра)

Переименование записанная — это унарная операция, как $\rho _{a/b}(R)$ где результат идентичен R, за исключением того, что атрибут b во всех кортежах переименован в атрибут a . Это просто используется для переименования атрибута отношения или самого отношения.

Чтобы переименовать атрибут «isFriend» в «isBusinessContact» в отношении, $\rho _{\text{isBusinessContact / isFriend}}({\text{addressBook}})$ может быть использован.

Существует также $\rho _{x(A_{1},\ldots ,A_{n})}(R)$ обозначение, где R переименован в x , а атрибуты $\{a_{1},\ldots ,a_{n}\}$ переименованы в $\{A_{1},\ldots ,A_{n}\}$.

Соединения и подобные им операторы

Естественное соединение (⨝)

«Естественное соединение» перенаправляется сюда. Информацию о реализации SQL см. в разделе Естественное соединение (SQL) .

«⋈» перенаправляется сюда. Информацию о группе, иногда обозначаемой этим символом, см. в The Armed .

Естественное соединение (⨝) — это бинарный оператор , который записывается как ( R ⨝ S ), где R и S — отношения . Результатом естественного соединения является набор всех комбинаций кортежей в R и S , которые имеют одинаковые имена общих атрибутов. В качестве примера рассмотрим таблицы «Сотрудник» и «Отдел» и их естественное соединение:

Сотрудник

Имя	Эмпид	Название отдела
Гарри	3415	Финансы
Салли	2241	Продажи
Джордж	3401	Финансы
Гарриет	2202	Продажи
Мэри	1257	Человеческие ресурсы

Отдел

Название отдела	Менеджер
Финансы	Джордж
Продажи	Гарриет
Производство	Чарльз

Сотрудник ⨝ Отдела

Имя	Эмпид	Название отдела	Менеджер
Гарри	3415	Финансы	Джордж
Салли	2241	Продажи	Гарриет
Джордж	3401	Финансы	Джордж
Гарриет	2202	Продажи	Гарриет

Обратите внимание, что в результате не отображаются ни сотрудник по имени Мэри, ни производственный отдел.

Это также можно использовать для определения состава отношений . Например, состав сотрудников и отделов — это их объединение, как показано выше, проецируемое на все атрибуты, кроме общего атрибута DeptName . В теории категорий соединение представляет собой в точности произведение расслоений .

Естественное соединение, возможно, является одним из наиболее важных операторов, поскольку оно является реляционным аналогом логического оператора И. Обратите внимание, что если одна и та же переменная появляется в каждом из двух предикатов, соединенных оператором И, то эта переменная обозначает одно и то же, и оба появления всегда должны быть заменены одним и тем же значением (это следствие идемпотентности логического И). . В частности, естественное соединение позволяет комбинировать отношения, связанные внешним ключом . Например, в приведенном выше примере внешний ключ, вероятно, принадлежит сотруднику . DeptName в Dept. ​ DeptName , а затем естественное объединение сотрудников и отделов объединяет всех сотрудников с их отделами. Это работает, поскольку внешний ключ сохраняется между атрибутами с одинаковым именем. Если это не так, как, например, во внешнем ключе Dept. из Менеджер для сотрудника . Name , то эти столбцы необходимо переименовать перед естественным объединением. Такое соединение иногда также называют равносоединением ( см. θ -соединение).

Более формально семантика естественного соединения определяется следующим образом:

$R\bowtie S=\left\{r\cup s\ \vert \ r\in R\ \land \ s\in S\ \land \ {\mathit {Fun}}(r\cup s)\right\}$ ( 1 )

где Fun(t) — предикат , который истинен для отношения t (в математическом смысле), если и только если t — функция (т. е. t не отображает какой-либо атрибут в несколько значений). Обычно требуется, чтобы R и S имели хотя бы один общий атрибут, но если это ограничение опущено и R и S не имеют общих атрибутов, то естественное соединение становится в точности декартовым произведением.

Естественное соединение можно смоделировать с помощью примитивов Кодда следующим образом. Предположим, что c ₁ ,..., cm _– имена атрибутов, общие для R и S , r ₁ ,..., r _n – это имена атрибутов, уникальные для R и s ₁ ,..., sk _, являются имена атрибутов, уникальные для S . Кроме того, предположим, что имена атрибутов x ₁ ,..., x _m не находятся ни в R, ни в S . На первом этапе общие имена атрибутов в S можно переименовать :

$T=\rho _{x_{1}/c_{1},\ldots ,x_{m}/c_{m}}(S)=\rho _{x_{1}/c_{1}}(\rho _{x_{2}/c_{2}}(\ldots \rho _{x_{m}/c_{m}}(S)\ldots ))$ ( 2 )

Затем мы берем декартово произведение и выбираем кортежи, которые необходимо соединить:

$P=\sigma _{c_{1}=x_{1},\ldots ,c_{m}=x_{m}}(R\times T)=\sigma _{c_{1}=x_{1}}(\sigma _{c_{2}=x_{2}}(\ldots \sigma _{c_{m}=x_{m}}(R\times T)\ldots ))$ ( 3 )

Наконец, мы делаем проекцию, чтобы избавиться от переименованных атрибутов:

$U=\Pi _{r_{1},\ldots ,r_{n},c_{1},\ldots ,c_{m},s_{1},\ldots ,s_{k}}(P)$ ( 4 )

θ -соединение и равносоединение

Рассмотрим таблицы «Автомобиль» и «Лодка» , в которых перечислены модели автомобилей и лодок и соответствующие цены. Предположим, клиентка хочет купить машину и лодку, но не хочет тратить на лодку больше денег, чем на машину. θ ≥ -соединение (⋈ _θ ) по предикату CarPrice создает сглаженные пары строк , BoatPrice которые удовлетворяют предикату. При использовании условия, в котором атрибуты равны, например Цена, условие можно указать как Цена = Цена. или, альтернативно, ( Цена ).

Машина

Модель автомобиля	АвтомобильЦена
Метод	20,000
КарБ	30,000
АвтомобильC	50,000

Лодка

Модель Лодки	ЛодкаЦена
Лодка1	10,000
Лодка2	40,000
Лодка3	60,000

${Car\bowtie Boat \atop \scriptstyle CarPrice\geq BoatPrice}$

Модель автомобиля	АвтомобильЦена	Модель Лодки	ЛодкаЦена
Метод	20,000	Лодка1	10,000
КарБ	30,000	Лодка1	10,000
АвтомобильC	50,000	Лодка1	10,000
АвтомобильC	50,000	Лодка2	40,000

Чтобы объединить кортежи из двух отношений, где условием объединения является не просто равенство общих атрибутов, удобно иметь более общую форму оператора соединения, которая представляет собой θ -соединение (или тета-соединение). θ - соединение — это бинарный оператор, который записывается как ${R\ \bowtie \ S \atop a\ \theta \ b}$ или ${R\ \bowtie \ S \atop a\ \theta \ v}$ где a и b — имена атрибутов, θ — бинарный оператор отношения в множестве {<, ≤, =, ≠, >, ≥ }, υ — константа значения, а R и S — отношения. Результатом этой операции являются все комбинации кортежей из R и S, удовлетворяющие θ . Результат θ -соединения определяется только в том случае, если заголовки S и R не пересекаются, то есть не содержат общего атрибута.

Таким образом, моделирование этой операции в основных операциях выглядит следующим образом:

р ⋈ _θ S знак равно σ _θ ( р × S )

Если оператор θ является оператором равенства (=), то это соединение также называется эквисоединением .

Обратите внимание, однако, что компьютерный язык, поддерживающий операторы естественного соединения и выбора, также не требует θ -соединения, поскольку этого можно достичь путем выбора из результата естественного соединения (которое вырождается в декартово произведение, когда нет общих атрибуты).

В реализациях SQL соединение по предикату обычно называется внутренним соединением , а ключевое слово on позволяет указать предикат, используемый для фильтрации строк. Важно отметить: формирование плоского декартова произведения с последующей фильтрацией строк концептуально правильно, но реализация будет использовать более сложные структуры данных для ускорения запроса на соединение.

Полусоединение (⋉ и ⋊)

Левое полусоединение — это соединение, аналогичное естественному соединению и записываемое как $R\ltimes S$ где $R$ и $S$ являются отношениями . Результатом является набор всех кортежей в $R$ для которого есть кортеж в $S$ которые совпадают по именам их общих атрибутов. Отличие от естественного соединения состоит в том, что другие столбцы $S$ не появляются. Например, рассмотрим таблицы «Сотрудник» и «Отдел» и их полусоединение:

Сотрудник

Имя	Эмпид	Название отдела
Гарри	3415	Финансы
Салли	2241	Продажи
Джордж	3401	Финансы
Гарриет	2202	Производство

Отдел

Название отдела	Менеджер
Продажи	Салли
Производство	Гарриет

Сотрудник ⋉ Отдел

Имя	Эмпид	Название отдела
Салли	2241	Продажи
Гарриет	2202	Производство

Более формально семантику полусоединения можно определить как следует:

$R\ltimes S=\{t:t\in R\land \exists s\in S(\operatorname {Fun} (t\cup s))\}$

где $\operatorname {Fun} (r)$ такое же, как в определении естественного соединения.

Полусоединение можно смоделировать с использованием естественного соединения следующим образом. Если $a_{1},\ldots ,a_{n}$ являются именами атрибутов $R$, затем

$R\ltimes S=\Pi _{a_{1},\ldots ,a_{n}}(R\bowtie S).$

Поскольку мы можем моделировать естественное соединение с помощью базовых операторов, отсюда следует, что это справедливо и для полусоединения.

В статье Кодда 1970 года полусоединение называется ограничением.

Антисоединение (▷)

Антисоединение, записанное как R ▷ S , где R и S — отношения , аналогично полусоединению, но результатом антиобъединения являются только те кортежи в R , для которых нет кортежа в S, равного по именам их общих атрибутов.

В качестве примера рассмотрим таблицы «Сотрудник» и «Отдел» и их антисоединение:

Сотрудник

Имя	Эмпид	Название отдела
Гарри	3415	Финансы
Салли	2241	Продажи
Джордж	3401	Финансы
Гарриет	2202	Производство

Отдел

Название отдела	Менеджер
Продажи	Салли
Производство	Гарриет

Сотрудник ▷ Отдел

Имя	Эмпид	Название отдела
Гарри	3415	Финансы
Джордж	3401	Финансы

Антисоединение формально определяется следующим образом:

р ▷ S знак равно { т : т ∈ R ∧ ¬∃ s ∈ S ( Fun ( т ∪ s )) }

или

R ▷ S = { t : t ∈ R , не существует кортежа s из S , который удовлетворяет условию Fun ( t ∪ s ) }

где Fun ( t ∪ s ) соответствует определению естественного соединения.

Антисоединение также можно определить как дополнение полусоединения следующим образом:

р ▷ С знак равно р - р ⋉ С ( 5 )

Учитывая это, анти-соединение иногда называют анти-полусоединением, а оператор анти-соединения иногда записывается как символ полусоединения с чертой над ним вместо ▷.

В случае, когда отношения имеют одинаковые атрибуты (совместимые по объединению), антисоединение равно минусу.

Дивизион (÷)

Деление — это бинарная операция, которая записывается R ÷ S. как Деление не реализовано непосредственно в SQL. Результат состоит из ограничений кортежей в R на имена атрибутов, уникальные для R , т. е. в заголовке R но не в заголовке S , для чего считается, что все их комбинации с кортежами в S присутствуют в R. , Для примера см. таблицы Completed , DBProject и их разделение:

Завершенный

Студент	Задача
Фред	База данных1
Фред	База данных2
Фред	Компилятор1
Евгений	База данных1
Евгений	Компилятор1
Сара	База данных1
Сара	База данных2

ДБПроект

Задача
База данных1
База данных2

Завершено ÷ DBProject

Студент
Фред
Сара

Если DBProject содержит все задачи проекта «База данных», то результат приведенного выше разделения содержит ровно тех студентов, которые выполнили обе задачи проекта «База данных». Более формально семантика деления определяется следующим образом:

р ÷ S знак равно { т [ а ₁ ,..., а _п ] : т ∈ R ∧ ∀ s ∈ S ( ( т [ а ₁ ,..., а _п ] ∪ s ) ∈ R ) } ( 6 )

где { a ₁ ,..., a _n } — набор имен атрибутов, уникальных для R , а t [ a ₁ ,..., ] _an — ограничение t на этот набор. Обычно требуется, чтобы имена атрибутов в заголовке S были подмножеством имен атрибутов R , поскольку в противном случае результат операции всегда будет пустым.

Моделирование деления с основными операциями происходит следующим образом. Мы предполагаем, что a ₁ ,..., an _— имена атрибутов, уникальные для R , а b ₁ ,..., b _m — имена атрибутов S . На первом этапе мы проецируем R на его уникальные имена атрибутов и создаем все комбинации с кортежами в S :

Т := π _{а 1 ,..., а п} ( р ) × S

В предыдущем примере T будет представлять таблицу, в которой каждый студент (поскольку студент является уникальным ключом/атрибутом таблицы «Завершено») сочетается с каждой заданной задачей. Так, например, у Юджина в T будет две строки: Юджин → База данных1 и Юджин → База данных2.

ЭГ: Во-первых, давайте представим, что у «Завершено» есть третий атрибут, называемый «оценка». Это нежелательный багаж, поэтому мы всегда должны его проецировать. Фактически, на этом этапе мы также можем удалить «Задачу» из R; умножение возвращает его обратно.

T := π _Student ( R ) × S // Это дает нам все возможные желаемые комбинации, включая те, которые на самом деле не существуют в R, и исключая другие (например, Фред | компилятор1, который не является желаемой комбинацией)

Т

Студент	Задача
Фред	База данных1
Фред	База данных2
Евгений	База данных1
Евгений	База данных2
Сара	База данных1
Сара	База данных2

На следующем шаге мы вычитаем R из T

отношение :

У := Т - Р

В U у нас есть возможность комбинации, которые «могли» быть в R , но не были.

ЭГ: И снова про проекции: T и R должны иметь одинаковые имена/заголовки атрибутов.

U := T − π _Student,Task ( R ) // Это дает нам список того, чего не хватает.

Т

Студент	Задача
Фред	База данных1
Фред	База данных2
Евгений	База данных1
Евгений	База данных2
Сара	База данных1
Сара	База данных2

R ака Завершено

Студент	Задача
Фред	База данных1
Фред	База данных2
Фред	Компилятор1
Евгений	База данных1
Евгений	Компилятор1
Сара	База данных1
Сара	База данных2

В

он же

Т - Р

он же

чего не хватает

Студент	Задача
Евгений	База данных2

Итак, если мы теперь возьмем проекцию имен атрибутов, уникальных для R

тогда у нас есть ограничения кортежей в R, для которых не все комбинации с кортежами в S присутствовали в R :

V := π _{а 1 ,..., а п} ( U )

ПРИМЕР: Проект U вплоть до рассматриваемых атрибутов (Студент)

V  := π _Student ( U )

V

Студент
Евгений

Итак, что осталось сделать, так это взять проекцию R на его уникальные имена атрибутов и вычтите их из V :

W := π _{а 1 ,..., а п} ( р ) - V

EG: W  := π _Student ( R ) − V .

πСтудент ₎ ( Р

Студент
Фред
Евгений
Сара

V

Студент
Евгений

В

он же

(π _Student ( R ) − V )

он же

желаемый результат

Студент
Фред
Сара

Общие расширения

На практике описанная выше классическая реляционная алгебра расширяется за счет различных операций, таких как внешние соединения, агрегатные функции и даже транзитивное замыкание.

Внешние соединения

См. также: Соединение (SQL) § Внешнее соединение.

В то время как результат соединения (или внутреннего соединения) состоит из кортежей, образованных путем объединения совпадающих кортежей в двух операндах, внешнее соединение содержит эти кортежи и, кроме того, некоторые кортежи, образованные путем расширения несовпадающего кортежа в одном из операндов путем «заполнения» значений. для каждого из атрибутов другого операнда. Внешние соединения не считаются частью обсуждавшейся до сих пор классической реляционной алгебры.

Операторы, определенные в этом разделе, предполагают существование нулевого значения ω , которое мы не определяем и которое будет использоваться для значений заполнения; на практике это соответствует NULL в SQL. Чтобы сделать последующие операции выбора в результирующей таблице значимыми, значениям NULL необходимо присвоить семантическое значение; в подходе Кодда пропозициональная логика, используемая при выборе, расширена до трехзначной логики , хотя в этой статье мы опускаем эти детали.

Определены три оператора внешнего соединения: левое внешнее соединение, правое внешнее соединение и полное внешнее соединение. (Слово «внешний» иногда опускается.)

Левое внешнее соединение (⟕)

Левое внешнее соединение записывается как R ⟕ S, где R и S — отношения . Результатом левого внешнего соединения является набор всех комбинаций кортежей в R и S , которые имеют одинаковые имена общих атрибутов, а также (грубо говоря) кортежей в , у которых нет совпадающих кортежей в S. R

В качестве примера рассмотрим таблицы «Сотрудник» и «Отдел» и их левое внешнее соединение:

Сотрудник

Имя	Эмпид	Название отдела
Гарри	3415	Финансы
Салли	2241	Продажи
Джордж	3401	Финансы
Гарриет	2202	Продажи
Тим	1123	Исполнительный

Отдел

Название отдела	Менеджер
Продажи	Гарриет
Производство	Чарльз

Сотрудник ⟕ Отдела

Имя	Эмпид	Название отдела	Менеджер
Гарри	3415	Финансы	ой
Салли	2241	Продажи	Гарриет
Джордж	3401	Финансы	ой
Гарриет	2202	Продажи	Гарриет
Тим	1123	Исполнительный	ой

В результирующем отношении кортежи в S, которые не имеют общих значений в именах общих атрибутов с кортежами в R, принимают нулевое значение ω .

нет кортежей Поскольку в Dept с DeptName of Finance или Executive , ω в результирующем отношении встречаются , где кортежи в Employer имеют DeptName of Finance или Executive .

Пусть r ₁ , r ₂ , ..., r _n — атрибуты отношения R и пусть {( ω , ..., ω )} — одноэлементный элемент отношение на атрибутах, которые уникальны для отношения S (те, которые не являются атрибутами R ). Тогда левое внешнее соединение можно описать в терминах естественного соединения (и, следовательно, с использованием базовых операторов) следующим образом:

$(R\bowtie S)\cup ((R-\pi _{r_{1},r_{2},\dots ,r_{n}}(R\bowtie S))\times \{(\omega ,\dots ,\omega )\})$

Правое внешнее соединение (⟖)

Правое внешнее соединение ведет себя почти идентично левому внешнему объединению, но роли таблиц меняются.

Правое внешнее соединение R и S записывается как R ⟖ S. отношений Результатом правого внешнего соединения является набор всех комбинаций кортежей в R и S , которые имеют одинаковые имена общих атрибутов, в дополнение к кортежам в , у которых нет совпадающих кортежей в R. S

Например, рассмотрим таблицы «Сотрудник» и «Отдел» и их правое внешнее соединение:

Сотрудник

Имя	Эмпид	Название отдела
Гарри	3415	Финансы
Салли	2241	Продажи
Джордж	3401	Финансы
Гарриет	2202	Продажи
Тим	1123	Исполнительный

Отдел

Название отдела	Менеджер
Продажи	Гарриет
Производство	Чарльз

Сотрудник ⟖ Отдел

Имя	Эмпид	Название отдела	Менеджер
Салли	2241	Продажи	Гарриет
Гарриет	2202	Продажи	Гарриет
ой	ой	Производство	Чарльз

В результирующем отношении кортежи в R, которые не имеют общих значений в именах общих атрибутов с кортежами в S, принимают нулевое значение ω .

нет кортежей Поскольку в элементе Сотрудник с DeptName of Production , ω встречаются в атрибутах Name и EmpId результирующего отношения, тогда как кортежи в Dept имели DeptName of Production .

Пусть s ₁ , s ₂ , ..., s _n — атрибуты отношения S и пусть {( ω , ..., ω )} — одноэлементный элемент отношение на атрибутах, которые уникальны для отношения R (те, которые не являются атрибутами S ). Затем, как и в случае с левым внешним соединением, правое внешнее соединение можно смоделировать с использованием естественного соединения следующим образом:

$(R\bowtie S)\cup (\{(\omega ,\dots ,\omega )\}\times (S-\pi _{s_{1},s_{2},\dots ,s_{n}}(R\bowtie S)))$

Полное внешнее соединение (⟗)

Внешнее соединение или полное внешнее соединение фактически объединяет результаты левого и правого внешних соединений.

записывается как R⟗S , S где R и — отношения Полное внешнее соединение . Результатом полного внешнего соединения является набор всех комбинаций кортежей в R и S , которые равны по именам общих атрибутов, в дополнение к кортежам в S , у которых нет совпадающих кортежей в R, и кортежам в R , у которых нет совпадающих кортежей. в S в именах их общих атрибутов.

В качестве примера рассмотрим таблицы «Сотрудник» и «Отдел» и их полное внешнее соединение:

Сотрудник

Имя	Эмпид	Название отдела
Гарри	3415	Финансы
Салли	2241	Продажи
Джордж	3401	Финансы
Гарриет	2202	Продажи
Тим	1123	Исполнительный

Отдел

Название отдела	Менеджер
Продажи	Гарриет
Производство	Чарльз

Сотрудник ⟗ Отдел

Имя	Эмпид	Название отдела	Менеджер
Гарри	3415	Финансы	ой
Салли	2241	Продажи	Гарриет
Джордж	3401	Финансы	ой
Гарриет	2202	Продажи	Гарриет
Тим	1123	Исполнительный	ой
ой	ой	Производство	Чарльз

В результирующем отношении кортежи в R, которые не имеют общих значений в именах общих атрибутов с кортежами в S, принимают нулевое значение ω . Кортежи в S, которые не имеют общих значений в именах общих атрибутов с кортежами в R, также принимают нулевое значение ω .

Полное внешнее соединение можно смоделировать с использованием левого и правого внешних соединений (и, следовательно, естественного соединения и объединения множеств) следующим образом:

р ⟗ S знак равно ( р ⟕ S ) ∪ ( р ⟖ S )

Операции для вычислений предметной области

В реляционной алгебре пока не представлено ничего, что позволяло бы выполнять вычисления в областях данных (кроме вычисления пропозициональных выражений, содержащих равенство). Например, невозможно, используя только введенную до сих пор алгебру, написать выражение, которое умножало бы числа из двух столбцов, например, цену за единицу товара на количество, чтобы получить общую цену. Практические языки запросов имеют такие возможности, например SQL SELECT позволяет арифметическим операциям определять новые столбцы в результате. SELECT unit_price * quantity AS total_price FROM t, и аналогичная возможность более подробно представлена ​​в Tutorial D. EXTEND ключевое слово. В теории баз данных это называется расширенной проекцией .

Агрегация

Более того, вычисление различных функций над столбцом, например суммирование его элементов, также невозможно с использованием введенной до сих пор реляционной алгебры. В большинство систем реляционных баз данных включены пять агрегатных функций . Этими операциями являются сумма, счет, среднее, максимум и минимум. В реляционной алгебре операция агрегирования над схемой ( A ₁ , A ₂ , ... An ₎ записывается следующим образом:

$G_{1},G_{2},\ldots ,G_{m}\ g_{f_{1}({A_{1}}'),f_{2}({A_{2}}'),\ldots ,f_{k}({A_{k}}')}\ (r)$

где каждый A _j ', 1 ≤ j ≤ k , является одним из исходных атрибутов A _i , 1 ≤ i ≤ n .

Атрибуты, предшествующие g, являются атрибутами группировки, которые действуют как предложение «группировать по» в SQL. Затем к отдельным атрибутам применяется произвольное количество функций агрегирования. Операция применяется к произвольному отношению r . Атрибуты группировки являются необязательными, и если они не указаны, функции агрегирования применяются ко всему отношению, к которому применяется операция.

Предположим, у нас есть таблица с именем Счет с тремя графами, а именно Account_Number, Branch_Name и Баланс . Мы хотим найти максимальный баланс каждой ветви. Это достигается за счет _{Имя_филиала} G _{Макс( Баланс )} ( Счет ). Чтобы найти наибольший баланс всех счетов независимо от филиала, мы могли бы просто написать G _{Max( Баланс )} ( Счет ).

Группировку часто записывают как _{Имя_филиала} ɣ _{Макс( Баланс )} ( Учетная запись ) вместо этого.

Транзитивное замыкание

Хотя реляционная алгебра кажется достаточно мощной для большинства практических целей, существуют некоторые простые и естественные операторы отношений , которые не могут быть выражены с помощью реляционной алгебры. Одним из них является транзитивное замыкание бинарного отношения. Для заданной области D пусть бинарное отношение R является подмножеством D × D . Транзитивное замыкание R ⁺ R — это наименьшее подмножество D × D , содержащее R и удовлетворяющее следующему условию:

$\forall x\forall y\forall z\left((x,y)\in R^{+}\wedge (y,z)\in R^{+}\Rightarrow (x,z)\in R^{+}\right)$

Это можно доказать, используя тот факт, что не существует выражения реляционной алгебры E ( R ), принимающего R в качестве переменного аргумента, которое производит R ⁺ .

Однако SQL официально поддерживает такие запросы с фиксированными точками с 1999 года, и задолго до этого у него были расширения в этом направлении, специфичные для конкретного поставщика.

Использование алгебраических свойств для оптимизации запросов

Два возможных плана запроса для треугольного запроса R(A, B) ⋈ S(B, C) ⋈ T(A, C) ; первый сначала соединяет S и T и соединяет результат с R , второй сначала соединяет R и S и соединяет результат с T

Системы управления реляционными базами данных часто включают в себя оптимизатор запросов , который пытается определить наиболее эффективный способ выполнения данного запроса. Оптимизаторы запросов перебирают возможные планы запросов , оценивают их стоимость и выбирают план с наименьшей оценочной стоимостью. Если запросы представлены операторами реляционной алгебры, оптимизатор запросов может перечислить возможные планы запросов, переписав исходный запрос, используя алгебраические свойства этих операторов.

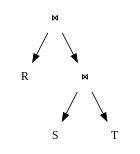
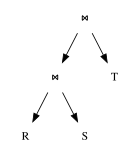
Запросы можно представить в виде дерева , где

• внутренние узлы являются операторами,
• листья-это отношения ,
• поддеревья являются подвыражениями.

Основная цель оптимизатора запросов — преобразовать деревья выражений в эквивалентные деревья выражений, в которых средний размер отношений, создаваемых подвыражениями в дереве, меньше, чем был до оптимизации . Вторичная цель — попытаться сформировать общие подвыражения в одном запросе или, если одновременно оценивается более одного запроса, во всех этих запросах. Обоснование второй цели заключается в том, что достаточно один раз вычислить общие подвыражения, и результаты можно использовать во всех запросах, содержащих это подвыражение.

Вот набор правил, которые можно использовать при таких преобразованиях.

Выбор

Правила, касающиеся операторов выбора, играют наиболее важную роль в оптимизации запросов. Выбор — это оператор, который очень эффективно уменьшает количество строк в своем операнде, поэтому, если выборки в дереве выражений перемещаются к листьям, внутренние связи (получаемые подвыражениями), скорее всего, уменьшатся.

Основные свойства выбора

Выбор является идемпотентным (несколько применений одного и того же выбора не имеют дополнительного эффекта, кроме первого) и коммутативным (порядок применения выбора не влияет на конечный результат).

1. $\sigma _{A}(R)=\sigma _{A}\sigma _{A}(R)\,\!$
2. $\sigma _{A}\sigma _{B}(R)=\sigma _{B}\sigma _{A}(R)\,\!$

Разбивка выборок со сложными условиями

Выборка, условием которой является конъюнкция более простых условий, эквивалентна последовательности выборок с теми же отдельными условиями, а выборка, условием которой является дизъюнкция, эквивалентна объединению выборок. Эти идентификаторы можно использовать для объединения выборок, чтобы нужно было оценивать меньшее количество выборок, или для их разделения, чтобы выборки компонентов можно было перемещать или оптимизировать отдельно.

1. $\sigma _{A\land B}(R)=\sigma _{A}(\sigma _{B}(R))=\sigma _{B}(\sigma _{A}(R))$
2. $\sigma _{A\lor B}(R)=\sigma _{A}(R)\cup \sigma _{B}(R)$

Выбор и перекрестное произведение

Перекрестное произведение — самый затратный оператор для оценки. Если входные отношения имеют N и M строк, результат будет содержать $NM$ ряды. Поэтому важно уменьшить размер обоих операндов перед применением оператора перекрестного произведения.

Это можно эффективно сделать, если за векторным произведением следует оператор выбора, например $\sigma _{A}(R\times P)$. Учитывая определение соединения, это наиболее вероятный случай. Если за векторным произведением не следует оператор выбора, мы можем попытаться перенести выборку с более высоких уровней дерева выражений, используя другие правила выбора.

В приведенном выше случае условие A разбивается на условия B , C и D с использованием правил разделения для сложных условий выбора, так что $A=B\wedge C\wedge D$ и B содержит атрибуты только из R , C атрибуты только из P , а D содержит часть A , которая содержит атрибуты как из R, так и из P. содержит Обратите внимание, что B , C или D возможно пусты. Тогда имеет место следующее:

$\sigma _{A}(R\times P)=\sigma _{B\wedge C\wedge D}(R\times P)=\sigma _{D}(\sigma _{B}(R)\times \sigma _{C}(P))$

Операторы выбора и установки

Выбор является дистрибутивным по операторам разности множеств, пересечения и объединения. Следующие три правила используются для перемещения выбора ниже операций над множествами в дереве выражений. Для операторов разности множеств и операторов пересечения можно применить оператор выбора только к одному из операндов после преобразования. Это может быть полезно, если один из операндов мал и затраты на вычисление оператора выбора перевешивают преимущества использования меньшего отношения в качестве операнда.

1. $\sigma _{A}(R\setminus P)=\sigma _{A}(R)\setminus \sigma _{A}(P)=\sigma _{A}(R)\setminus P$
2. $\sigma _{A}(R\cup P)=\sigma _{A}(R)\cup \sigma _{A}(P)$
3. $\sigma _{A}(R\cap P)=\sigma _{A}(R)\cap \sigma _{A}(P)=\sigma _{A}(R)\cap P=R\cap \sigma _{A}(P)$

Выбор и проекция

Выбор коммутирует с проекцией тогда и только тогда, когда поля, на которые ссылаются условия выбора, являются подмножеством полей в проекции. Выполнение выбора перед проецированием может быть полезно, если операнд является перекрестным произведением или соединением. В других случаях, если вычисление условия выбора является относительно дорогостоящим, перемещение выбора за пределы проекции может уменьшить количество кортежей, которые необходимо проверить (поскольку проекция может создавать меньше кортежей из-за исключения дубликатов, возникающих из-за пропущенных полей).

$\pi _{a_{1},\ldots ,a_{n}}(\sigma _{A}(R))=\sigma _{A}(\pi _{a_{1},\ldots ,a_{n}}(R)){\text{ where fields in }}A\subseteq \{a_{1},\ldots ,a_{n}\}$

Проекция

Основные свойства проекции

Проекция идемпотентна, так что серия (действительных) проекций эквивалентна самой внешней проекции.

$\pi _{a_{1},\ldots ,a_{n}}(\pi _{b_{1},\ldots ,b_{m}}(R))=\pi _{a_{1},\ldots ,a_{n}}(R){\text{ where }}\{a_{1},\ldots ,a_{n}\}\subseteq \{b_{1},\ldots ,b_{m}\}$

Операторы проекции и множества

Проекция дистрибутивна по объединению множеств.

$\pi _{a_{1},\ldots ,a_{n}}(R\cup P)=\pi _{a_{1},\ldots ,a_{n}}(R)\cup \pi _{a_{1},\ldots ,a_{n}}(P).\,$

Проекция не распределяется по пересечению и заданной разнице. Контрпримеры дают:

$\pi _{A}(\{\langle A=a,B=b\rangle \}\cap \{\langle A=a,B=b'\rangle \})=\emptyset$

$\pi _{A}(\{\langle A=a,B=b\rangle \})\cap \pi _{A}(\{\langle A=a,B=b'\rangle \})=\{\langle A=a\rangle \}$

и

$\pi _{A}(\{\langle A=a,B=b\rangle \}\setminus \{\langle A=a,B=b'\rangle \})=\{\langle A=a\rangle \}$

$\pi _{A}(\{\langle A=a,B=b\rangle \})\setminus \pi _{A}(\{\langle A=a,B=b'\rangle \})=\emptyset \,,$

где b предполагается отличным от b' .

Переименовать

Основные свойства переименования

Последовательные переименования переменной можно объединить в одно переименование. Операции переименования, которые не имеют общих переменных, могут быть произвольно переупорядочены относительно друг друга, что можно использовать для объединения последовательных переименований, чтобы их можно было свернуть.

1. $\rho _{a/b}(\rho _{b/c}(R))=\rho _{a/c}(R)\,\!$
2. $\rho _{a/b}(\rho _{c/d}(R))=\rho _{c/d}(\rho _{a/b}(R))\,\!$

Переименование и установка операторов

Переименование является распределительным по разнице множеств, объединению и пересечению.

1. $\rho _{a/b}(R\setminus P)=\rho _{a/b}(R)\setminus \rho _{a/b}(P)$
2. $\rho _{a/b}(R\cup P)=\rho _{a/b}(R)\cup \rho _{a/b}(P)$
3. $\rho _{a/b}(R\cap P)=\rho _{a/b}(R)\cap \rho _{a/b}(P)$

Продукт и союз

Декартово произведение является распределительным по сравнению с объединением.

1. $(A\times B)\cup (A\times C)=A\times (B\cup C)$

Реализации

Первым языком запросов, основанным на алгебре Кодда, был Alpha, разработанный самим доктором Коддом. Впоследствии был создан ISBL , и эта новаторская работа получила признание многих авторитетов. как показывающий способ превратить идею Кодда в полезный язык. Business System 12 была недолговечной отраслевой реляционной СУБД, последовавшей примеру ISBL.

В 1998 году Крис Дейт и Хью Дарвен предложили язык под названием Tutorial D, предназначенный для использования при обучении теории реляционных баз данных, и его язык запросов также основан на идеях ISBL. это реализация Tutorial D. Rel — Bmg — это реализация реляционной алгебры в Ruby, которая точно следует принципам Tutorial D и The Third Manifesto .

Даже язык запросов SQL в общих чертах основан на реляционной алгебре, хотя операнды в SQL ( таблицы ) не являются в точности отношениями , и некоторые полезные теоремы о реляционной алгебре не выполняются в аналоге SQL (возможно, в ущерб оптимизаторам и/или оптимизаторам). или пользователей). Модель таблицы SQL представляет собой пакет ( мультмножество ), а не набор. Например, выражение $(R\cup S)\setminus T=(R\setminus T)\cup (S\setminus T)$ это теорема для реляционной алгебры на множествах, но не для реляционной алгебры на мешках; описание реляционной алгебры на мешках см. в главе 5 «Полного» учебника Гарсиа-Молины , Ульмана и Видома .

См. также

• Декартово произведение
• D4 (язык программирования) (реализация D)
• База данных
• Логика родственников
• Объектно-ролевое моделирование
• Проекция (математика)
• Проекция (реляционная алгебра)
• Проекция (теория множеств)
• Связь
• Связь (база данных)
• Алгебра отношений
• Композиция отношений
• Построение отношений
• Реляционное исчисление
• Реляционная база данных
• Реляционная модель
• Теория отношений
• Триадное отношение
• Кортежное реляционное исчисление
• SQL
• Ученый-компьютерщик
• Теорема Кодда

Дальнейшее чтение

Практически любой академический учебник по базам данных подробно описывает классическую реляционную алгебру.

• Имелинский, Т. ; Липски, В. (1984). «Реляционная модель данных и цилиндрические алгебры» . Журнал компьютерных и системных наук . 28 : 80–102. дои : 10.1016/0022-0000(84)90077-1 . (Для связи с цилиндрическими алгебрами ).

Внешние ссылки

• RAT Relational Algebra Translator Бесплатное программное обеспечение для преобразования реляционной алгебры в SQL
• Видеолекции: Обработка реляционной алгебры . Введение в то, как системы баз данных обрабатывают реляционную алгебру.
• Конспект лекций: Реляционная алгебра – краткое руководство по адаптации SQL-запросов к реляционной алгебре.
• Реляционная - графическая реализация реляционной алгебры.
• Оптимизация запросов . Эта статья представляет собой введение в использование реляционной алгебры для оптимизации запросов и включает многочисленные цитаты для более глубокого изучения.
• Система реляционной алгебры для Oracle и Microsoft SQL Server
• Pireal — экспериментальный образовательный инструмент для работы с реляционной алгеброй.
• DES – образовательный инструмент для работы с реляционной алгеброй и другими формальными языками.
• RelaX - Калькулятор реляционной алгебры (программное обеспечение с открытым исходным кодом, доступное в виде онлайн-сервиса без регистрации)
• РА: интерпретатор реляционной алгебры
• Перевод SQL в реляционную алгебру