Функционально-ориентированное программирование

В компьютерном программировании функционально -ориентированное программирование ( FOP ) или функционально-ориентированная разработка программного обеспечения ( FOSD ) — это парадигма программирования для создания программ в линейках программных продуктов (SPL) и для поэтапной разработки программ.

История [ править ]

вертикальное наложение слоев — Связь между стеками слоев и композициями трансформации

FOSD возник из многоуровневых конструкций и уровней абстракции сетевых протоколов и расширяемых систем баз данных в конце 1980-х годов. ^[1]Программа представляла собой стопку слоев. Каждый слой добавлял функциональность ранее составленным слоям, а разные композиции слоев создавали разные программы. Неудивительно, что для выражения таких замыслов возникла необходимость в компактном языке. Элементарная алгебра отвечала всем требованиям: каждый уровень представлял собой функцию ( преобразование программы ), которая добавляла новый код к существующей программе для создания новой программы, а конструкция программы моделировалась выражением, т. е. композицией преобразований (слоев). На рисунке слева показано расположение слоев i, j и h (где h находится внизу, а i — вверху). Для выражения этих планов использовались алгебраические обозначения i(j(h)), i•j•h и i+j+h.

Со временем слои стали приравниваться к функциям, где функция — это расширение функциональности программы. Было признано, что парадигма проектирования и создания программ является результатом оптимизации реляционных запросов, где программы оценки запросов определялись как выражения реляционной алгебры, а оптимизация запросов была оптимизацией выражений. ^[2]Линейка программных продуктов — это семейство программ, каждая из которых имеет уникальный набор функций. С тех пор FOSD превратился в изучение модульности функций, инструментов, анализа и методов проектирования для поддержки создания программ на основе функций.

Второе поколение исследований FOSD было посвящено взаимодействию функций, зародившемуся в сфере телекоммуникаций. термин « функционально-ориентированное программирование» ; Позже был придуман ^[3]эта работа выявила взаимодействие между слоями. Взаимодействия требуют адаптации функций при их сочетании с другими функциями.

Третье поколение исследований было сосредоточено на том факте, что каждая программа имеет несколько представлений (например, исходный код, make-файлы, документация и т. д.), и добавление функции в программу должно дорабатывать каждое из ее представлений, чтобы все они были согласованными. Кроме того, некоторые представления могут быть сгенерированы (или получены) из других. В разделах ниже представлена математика трёх последних поколений FOSD, а именно GenVoca , ^[1] ПРЕДСТОЯЩИЙ , ^[4] и ФОМДД ^[5]^[6]описаны и приведены ссылки на линейки продуктов, разработанных с использованием инструментов FOSD. Кроме того, ко всем поколениям FOSD применимы четыре дополнительных результата: метамодели FOSD , программные кубы FOSD и взаимодействие функций FOSD.

ГенВока [ править ]

GenVoca ( сумма названий Genesis и Avoca) ^[1]представляет собой композиционную парадигму для определения программ продуктовых линеек. Базовые программы представляют собой 0-арные функции или преобразования, называемые значениями :

f — базовая программа с функцией f
   h — базовая программа с функцией h

а функции — это унарные функции/преобразования, которые уточняют (модифицируют, расширяют, уточняют) программу:

i + x — добавляет функцию i в программу x
   j + x — добавляет функцию j в программу x.

где + обозначает композицию функции. Дизайн : программы — это именованное выражение, например

p ₁ = j + f -- программа p ₁ имеет функции j и f 
    p ₂ = j + h -- программа p ₂ имеет функции j и h 
    p ₃ = i + j + h — программа p ₃ имеет функции i, j и h.

Модель GenVoca предметной области или линейки программных продуктов представляет собой набор базовых программ и функций (см. Метамодели и программные кубы ). Программы (выражения), которые могут быть созданы, определяют линейку продуктов. Оптимизация выражений — это оптимизация конструкции программы , а оценка выражений — это генерация программы .

Примечание. GenVoca основана на поэтапной разработке программ: процессе, который подчеркивает простоту и понятность конструкции, которые являются ключом к пониманию программы и ее автоматизированному созданию. Рассмотрим программу p ₃ выше: она начинается с базовой программы h, затем добавляется функция j (читай: функциональность функции j добавляется в кодовую базу h) и, наконец, добавляется функция i (читай: функциональность функции i добавлено в кодовую базу j•h).

Примечание: не все комбинации функций имеют смысл. Модели признаков (которые можно перевести в пропозициональные формулы) представляют собой графические представления, определяющие допустимые комбинации признаков. ^[7]

Примечание. Более поздняя формулировка GenVoca симметрична : существует только одна базовая программа, 0 (пустая программа), и все функции являются унарными функциями. Это предполагает интерпретацию, согласно которой GenVoca составляет структуры программ путем суперпозиции , идею о том, что сложные структуры создаются путем наложения более простых структур. ^[8]^[9]Еще одна переформулировка GenVoca - это моноид : модель GenVoca представляет собой набор функций с операцией композиции (•); композиция ассоциативна и существует элемент идентичности (а именно 1, функция идентичности). Хотя все композиции возможны, не все они имеют смысл. Вот причина использования функциональных моделей .

Функции GenVoca изначально были реализованы с использованием препроцессора C ( #ifdef feature ... #endif) техники. Более продвинутая техника, называемая слоями миксинов , продемонстрировала связь функций с объектно-ориентированными проектами, основанными на совместной работе.

ВПЕРЕД [ править ]

Алгебраические иерархические уравнения для разработки приложений ( AHEAD ) ^[4]обобщил GenVoca двумя способами. Во-первых, была раскрыта внутренняя структура значений GenVoca в виде кортежей. Каждая программа имеет несколько представлений, таких как исходный код, документация, байт-код и файлы makefile. Значение GenVoca — это кортеж представлений программы. Например, в линейке анализаторов базовый анализатор f определяется его грамматикой g _f , исходным кодом Java s _f и документацией d _f . Парсер f моделируется кортежем f=[g _f , s _f , d _f ]. Каждое представление программы может иметь подпредставления, и они тоже могут иметь подпредставления рекурсивно. В общем, значение GenVoca представляет собой кортеж вложенных кортежей, которые определяют иерархию представлений для конкретной программы.

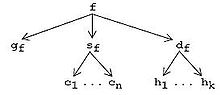
Иерархические отношения между программными артефактами

Пример. Предположим, что терминальные представления — это файлы. В AHEAD грамматика g _f соответствует одному файлу BNF, исходный файл s _f соответствует кортежу файлов Java [c ₁ …c _n ], а документация d _f представляет собой кортеж файлов HTML [h ₁ …h _k ]. Значение GenVoca (вложенные кортежи) можно изобразить в виде ориентированного графа: граф для парсера f показан на рисунке справа. Стрелки обозначают проекции, т. е. отображения кортежа на один из его компонентов. AHEAD реализует кортежи как файловые каталоги, поэтому f — это каталог, содержащий файл g _f и подкаталоги s _f и d _f . Аналогично, каталог s _f содержит файлы c ₁ …c _n , а каталог df содержит файлы h ₁ …h _k .

Примечание. Файлы можно дополнительно разложить по иерархии. Каждый класс Java можно разложить на кортеж членов и других объявлений классов (например, блоков инициализации и т. д.). Важная идея здесь заключается в том, что математика AHEAD рекурсивна.

Во-вторых, AHEAD выражает функции в виде вложенных кортежей унарных функций, называемых дельтами . Дельтами могут быть уточнения программы (преобразования, сохраняющие семантику), расширения (преобразования, расширяющие семантику), или взаимодействия (преобразования, изменяющие семантику). Мы используем нейтральный термин «дельта» для обозначения всех этих возможностей, поскольку каждая из них возникает при FOSD.

Для иллюстрации предположим, что функция j расширяет грамматику на Δg _j (добавляются новые правила и токены), расширяет исходный код на Δs _j (добавляются новые классы и члены и изменяются существующие методы) и расширяет документацию на Δd _j . Кортеж дельт для признака j моделируется j=[Δg _j , Δs _j , Δd _j ], который мы называем дельта-кортежом . Элементы дельта-кортежей сами могут быть дельта-кортежами. Пример: Δs _j представляет изменения, внесенные в каждый класс s _f признаком j, т.е. Δs _j =[Δc ₁ …Δc _n ]. Представления программы вычисляются рекурсивно путем сложения вложенных векторов. Представления для синтаксического анализатора p ₂ (выражение GenVoca которого равно j+f):

p ₂ = j + f -- выражение GenVoca 
       = [Δg _j , Δs _j , Δd _j ] + [g _f , s _f , d _f ] -- подстановка 
       = [Δg _j +g _f , Δs _j +s _f , Δd _j +d _f ] — составить кортежи поэлементно

То есть грамматика p ₂ является базовой грамматикой, составленной с ее расширением (Δg _j +g _f ), источником p ₂ является базовый источник, составленный с его расширением (Δs _j +s _f ), и так далее. Поскольку элементы дельта-кортежей сами могут быть дельта-кортежами, композиция рекурсивна, например, Δs _j +s _f = [Δc ₁ …Δc _n ]+[c ₁ …c _n ]=[Δc ₁ +c ₁ …Δc _n +c _n ]. Подводя итог, можно сказать, что значения GenVoca представляют собой вложенные кортежи программных артефактов, а функции — это вложенные дельта-кортежи, где + рекурсивно компонует их путем сложения векторов. В этом суть AHEAD.

Идеи, представленные выше, конкретно раскрывают два принципа FOSD. Принцип единообразия гласит, что все программные артефакты обрабатываются и изменяются одинаково. (Об этом свидетельствуют дельты для разных типов артефактов, приведенные выше). Принцип масштабируемости гласит, что все уровни абстракций обрабатываются одинаково. (Это приводит к иерархической вложенности кортежей выше).

Исходной реализацией AHEAD является набор инструментов AHEAD и язык Jak, который демонстрирует как принципы единообразия, так и масштабируемости. Инструменты нового поколения включают CIDE. ^[10] и FeatureHouse. ^[11]

ФОМДД [ править ]

Отношения вывода и уточнения между программными артефактами

Функционально-ориентированное модельно-ориентированное проектирование ( FOMDD ) ^[5]^[6]сочетает в себе идеи AHEAD с Model-Driven Design ( MDD ) (также известной как Model-Driven Architecture ( MDA )). Функции AHEAD фиксируют постоянное обновление артефактов программы при добавлении функции в программу. Но между программными артефактами, выражающими производные, существуют и другие функциональные связи. Например, связь между грамматикой g _f и ее источником синтаксического анализатора s _f определяется инструментом компилятора-компилятора, например, javacc. Аналогично, связь между исходным кодом Java s _f и его байт-кодом b _f определяется компилятором javac. Диаграмма поездок на работу отражает эти отношения. Объекты — это представления программы, стрелки вниз — это производные, а горизонтальные стрелки — это дельты. На рисунке справа показана коммутационная диаграмма для программы p ₃ = i+j+h = [g ₃ ,s ₃ ,b ₃ ].

Фундаментальным свойством коммутирующей диаграммы является то, что все пути между двумя объектами эквивалентны. Например, один из способов получить байт-код b ₃ синтаксического анализатора p ₃ (нижний правый объект на рисунке справа) из грамматики gh _{синтаксического} анализатора h (верхний левый объект) — это получить байт-код b _h и уточнить его до b _3. , а другой способ уточняет gh _до g ₃ , а затем выводит b ₃ , где + представляет дельта-композицию, а () — применение функции или инструмента:

б ₃ = Δb _j + Δb _i + javacc ( javac ( г _час ) ) = Javac ( javacc ( Δg _я + Δg _j + грамм _час ))

Есть ${\tbinom {4}{2}}$ возможные пути получения байт-кода b ₃ синтаксического анализатора p ₃ из грамматики gh _{синтаксического} анализатора h. Каждый путь представляет собой метапрограмму , выполнение которой генерирует целевой объект (b ₃ ) из начального объекта (g _f ). Существует потенциальная оптимизация: перемещение каждой стрелки коммутирующей диаграммы имеет свою стоимость. Самый дешевый (то есть кратчайший) путь между двумя объектами на коммутационной диаграмме — это геодезическая линия , которая представляет собой наиболее эффективную метапрограмму, создающую целевой объект из данного объекта.

Примечание. «Показатель затрат» не обязательно должен быть денежной величиной; Стоимость может измеряться временем производства, пиковыми или общими требованиями к памяти, энергопотреблением или каким-либо неформальным показателем, например «простотой объяснения», или комбинацией вышеперечисленного (например, многокритериальная оптимизация ). Идея геодезической является общей, и ее следует понимать и ценить в этом более общем контексте.

Примечание. На геодезической может быть m начальных и n конечных объектов; когда m=1 и n>1, это задача направленного дерева Штейнера , которая является NP-трудной.

Коммутирующие диаграммы важны как минимум по двум причинам: (1) существует возможность оптимизации генерации артефактов (например, геодезических) и (2) они определяют различные способы построения целевого объекта из исходного объекта. ^[5]^[12]Путь через диаграмму соответствует цепочке инструментов: чтобы модель FOMDD была согласованной, необходимо доказать (или продемонстрировать посредством тестирования), что все цепочки инструментов, которые сопоставляют один объект с другим, фактически дают эквивалентные результаты. Если это не так, то либо в одном или нескольких инструментах имеется ошибка, либо модель FOMDD неверна.

Примечание: приведенные выше идеи были вдохновлены теорией категорий . ^[5]^[6]

Приложения [ править ]

См. также [ править ]

Метамодели FOSD – продуктовые линейки продуктовых линеек
ФОСД оригами
Программные кубики FOSD – многомерные линейки продуктов
Язык программирования очень высокого уровня.

Ссылки [ править ]

^ Перейти обратно: ^а ^б ^с «Проектирование и реализация иерархических программных систем с повторно используемыми компонентами» (PDF) .
^ Выбор пути доступа в реляционных базах данных . 30 мая 1979 г., стр. 23–34. дои : 10.1145/582095.582099 . ISBN 9780897910019 . S2CID 8537523 .
^ «Функционально-ориентированное программирование: свежий взгляд на объекты» . Архивировано из оригинала 3 августа 2003 г. Проверено 16 декабря 2015 г.
^ Перейти обратно: ^а ^б «Масштабирование поэтапного уточнения» (PDF) .
^ Перейти обратно: ^а ^б ^с ^д «Функционально-ориентированная разработка на основе моделей: пример портлетов» (PDF) .
^ Перейти обратно: ^а ^б ^с Трухильо, Сальвадор; Азанза, Майдер; Диас, Оскар (октябрь 2007 г.). «Генеративное метапрограммирование» . Материалы 6-й международной конференции по генеративному программированию и компонентной инженерии . стр. 105–114. дои : 10.1145/1289971.1289990 . ISBN 9781595938558 . S2CID 236715 .
^ «Функциональные модели, грамматики и пропозициональные формулы» (PDF) .
^ «Алгебра функций и композиции функций» (PDF) .
^ «Наложение: независимый от языка подход к составлению программного обеспечения» (PDF) .
^ «Гарантия синтаксической правильности для всех вариантов линейки продуктов: языково-независимый подход» (PDF) .
^ «FeatureHouse: автоматизированная разработка программного обеспечения, не зависящая от языка» (PDF) .
^ «Тестирование линеек программных продуктов с использованием дополнительной генерации тестов» (PDF) .

[genvoca-1] Перейти обратно: ^а ^б ^с «Проектирование и реализация иерархических программных систем с повторно используемыми компонентами» (PDF) .

[selinger-2] Выбор пути доступа в реляционных базах данных . 30 мая 1979 г., стр. 23–34. дои : 10.1145/582095.582099 . ISBN 9780897910019 . S2CID 8537523 .

[FOP-3] «Функционально-ориентированное программирование: свежий взгляд на объекты» . Архивировано из оригинала 3 августа 2003 г. Проверено 16 декабря 2015 г.

[ahead-4] Перейти обратно: ^а ^б «Масштабирование поэтапного уточнения» (PDF) .

[fomdd-5] Перейти обратно: ^а ^б ^с ^д «Функционально-ориентированная разработка на основе моделей: пример портлетов» (PDF) .

[genmeta-6] Перейти обратно: ^а ^б ^с Трухильо, Сальвадор; Азанза, Майдер; Диас, Оскар (октябрь 2007 г.). «Генеративное метапрограммирование» . Материалы 6-й международной конференции по генеративному программированию и компонентной инженерии . стр. 105–114. дои : 10.1145/1289971.1289990 . ISBN 9781595938558 . S2CID 236715 .

[splc-7] «Функциональные модели, грамматики и пропозициональные формулы» (PDF) .

[amast08-8] «Алгебра функций и композиции функций» (PDF) .

[symmetric-9] «Наложение: независимый от языка подход к составлению программного обеспечения» (PDF) .

[CIDE-10] «Гарантия синтаксической правильности для всех вариантов линейки продуктов: языково-независимый подход» (PDF) .

[FH-11] «FeatureHouse: автоматизированная разработка программного обеспечения, не зависящая от языка» (PDF) .

[testing-12] «Тестирование линеек программных продуктов с использованием дополнительной генерации тестов» (PDF) .

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]