Функция распределения Вигнера

Анализ частотно-временного распределения WDF (красный и желтый) и банка FIR (зеленый).

Функция распределения Вигнера (WDF) используется при обработке сигналов в качестве преобразования в частотно-временном анализе .

WDF был впервые предложен в физике для учета квантовых поправок к классической статистической механике в 1932 году Юджином Вигнером , и он имеет важное значение для квантовой механики в фазовом пространстве (см., для сравнения: Распределение квазивероятностей Вигнера , также называемое Функция Вигнера или распределение Вигнера-Вилля ).

Учитывая общую алгебраическую структуру между сопряженными парами положение-импульс и частота-время , она также полезно используется при обработке сигналов в качестве преобразования в частотно-временном анализе, что является предметом этой статьи. По сравнению с кратковременным преобразованием Фурье , таким как преобразование Габора , функция распределения Вигнера обеспечивает максимально возможное временное и частотное разрешение, которое математически возможно в пределах ограничений принципа неопределенности. Обратной стороной является введение больших перекрестных членов между каждой парой компонентов сигнала, а также между положительными и отрицательными частотами, что делает исходную формулировку функции плохо подходящей для большинства приложений анализа. Были предложены последующие модификации, которые сохраняют точность функции распределения Вигнера, но в значительной степени подавляют перекрестные члены.

Математическое определение

Существует несколько различных определений функции распределения Вигнера. Данное здесь определение относится только к частотно-временному анализу. Учитывая временной ряд $x[t]$, его нестационарная функция автоковариации определяется выражением

$C_{x}(t_{1},t_{2})=\left\langle \left(x[t_{1}]-\mu [t_{1}]\right)\left(x[t_{2}]-\mu [t_{2}]\right)^{*}\right\rangle ,$

где $\langle \cdots \rangle$ обозначает среднее значение по всем возможным реализациям процесса и $\mu (t)$ это среднее значение, которое может быть или не быть функцией времени. Функция Вигнера $W_{x}(t,f)$ затем определяется путем выражения автокорреляционной функции через среднее время $t=(t_{1}+t_{2})/2$ и временной лаг $\tau =t_{1}-t_{2}$, а затем Фурье, преобразующее запаздывание.

$W_{x}(t,f)=\int _{-\infty }^{\infty }C_{x}\left(t+{\frac {\tau }{2}},t-{\frac {\tau }{2}}\right)\,e^{-2\pi i\tau f}\,d\tau .$

Таким образом, для одного временного ряда (среднее нулевое) функция Вигнера просто задается формулой

$W_{x}(t,f)=\int _{-\infty }^{\infty }x\left(t+{\frac {\tau }{2}}\right)\,x^{*}\left(t-{\frac {\tau }{2}}\right)\,e^{-2\pi i\tau f}\,d\tau .$

Мотивация использования функции Вигнера заключается в том, что она спектральной плотности . всегда сводится к функции $t$ для стационарных процессов, однако она полностью эквивалентна нестационарной автокорреляционной функции. Следовательно, функция Вигнера сообщает нам (примерно), как изменяется спектральная плотность во времени.

Пример частотно-временного анализа

Вот несколько примеров, иллюстрирующих, как WDF используется в частотно-временном анализе.

Постоянный входной сигнал

Когда входной сигнал постоянен, его частотно-временное распределение представляет собой горизонтальную линию вдоль оси времени. Например, если x ( t ) = 1, то

$W_{x}(t,f)=\int _{-\infty }^{\infty }e^{-i2\pi \tau \,f}\,d\tau =\delta (f).$

Синусоидальный входной сигнал

Когда входной сигнал представляет собой синусоидальную функцию, его частотно-временное распределение представляет собой горизонтальную линию, параллельную оси времени, смещенную от нее на частоту синусоидального сигнала. Например, если x ( t ) = e ^{i2π КТ} , затем

${\begin{aligned}W_{x}(t,f)&=\int _{-\infty }^{\infty }e^{i2\pi k\left(t+{\frac {\tau }{2}}\right)}e^{-i2\pi k\left(t-{\frac {\tau }{2}}\right)}e^{-i2\pi \tau \,f}\,d\tau \\&=\int _{-\infty }^{\infty }e^{-i2\pi \tau \left(f-k\right)}\,d\tau \\&=\delta (f-k).\end{aligned}}$

Входной сигнал чирпа

Когда входной сигнал представляет собой линейную функцию ЛЧМ , мгновенная частота является линейной функцией. Это означает, что частотно-временное распределение должно быть прямой линией. Например, если

$x(t)=e^{i2\pi kt^{2}}$ ,

то его мгновенная частота равна

${\frac {1}{2\pi }}{\frac {d(2\pi kt^{2})}{dt}}=2kt~,$

и его WDF

${\begin{aligned}W_{x}(t,f)&=\int _{-\infty }^{\infty }e^{i2\pi k\left(t+{\frac {\tau }{2}}\right)^{2}}e^{-i2\pi k\left(t-{\frac {\tau }{2}}\right)^{2}}e^{-i2\pi \tau \,f}\,d\tau \\&=\int _{-\infty }^{\infty }e^{i4\pi kt\tau }e^{-i2\pi \tau f}\,d\tau \\&=\int _{-\infty }^{\infty }e^{-i2\pi \tau (f-2kt)}\,d\tau \\&=\delta (f-2kt)~.\end{aligned}}$

Входной сигнал «Дельта»

Когда входной сигнал является дельта-функцией, поскольку он отличен от нуля только при t=0 и содержит бесконечные частотные компоненты, его частотно-временное распределение должно представлять собой вертикальную линию, пересекающую начало координат. Это означает, что частотно-временное распределение дельта-функции также должно быть дельта-функцией. Автор: ВДФ

${\begin{aligned}W_{x}(t,f)&=\int _{-\infty }^{\infty }\delta \left(t+{\frac {\tau }{2}}\right)\delta \left(t-{\frac {\tau }{2}}\right)e^{-i2\pi \tau \,f}\,d\tau \\&=4\int _{-\infty }^{\infty }\delta (2t+\tau )\delta (2t-\tau )e^{-i2\pi \tau f}\,d\tau \\&=4\delta (4t)e^{i4\pi tf}\\&=\delta (t)e^{i4\pi tf}\\&=\delta (t).\end{aligned}}$

Функция распределения Вигнера лучше всего подходит для частотно-временного анализа, когда фаза входного сигнала имеет 2-й порядок или ниже. Для этих сигналов WDF может точно генерировать частотно-временное распределение входного сигнала.

Функция товарного вагона

$x(t)={\begin{cases}1&|t|<1/2\\0&{\text{otherwise}}\end{cases}}\qquad$ ,

функция прямоугольная ⇒

$W_{x}(t,f)={\begin{cases}{\frac {1}{\pi f}}\sin(2\pi f\{1-2|t|\})&|t|<1/2\\0&{\mbox{otherwise}}\end{cases}}$

Перекрестное свойство

Функция распределения Вигнера не является линейным преобразованием. Перекрестный член («такты времени») возникает, когда во входном сигнале имеется более одного компонента, что аналогично биениям частоты по времени . в физике предков В квазивероятностном распределении Вигнера этот термин имеет важные и полезные физические последствия, необходимые для точных значений ожидания. Напротив, кратковременное преобразование Фурье не обладает этой особенностью. Отрицательные особенности WDF отражают предел Габора классического сигнала и физически не связаны с какой-либо возможной основой квантовой структуры.

Ниже приведены некоторые примеры, демонстрирующие перекрестную особенность функции распределения Вигнера.

• $x(t)={\begin{cases}\cos(2\pi t)&t\leq -2\\\cos(4\pi t)&-2<t\leq 2\\\cos(3\pi t)&t>2\end{cases}}$
• $x(t)=e^{it^{3}}$

Чтобы уменьшить перекрестные трудности, в литературе было предложено несколько подходов: некоторые из них приводят к новым преобразованиям, таким как модифицированная функция распределения Вигнера , преобразование Габора-Вигнера , функция распределения Чой-Вильямса и распределение классов Коэна .

функции

Функция распределения Вигнера имеет несколько очевидных свойств, перечисленных в следующей таблице.

Свойство проекции

${\begin{aligned}|x(t)|^{2}&=\int _{-\infty }^{\infty }W_{x}(t,f)\,df\\|X(f)|^{2}&=\int _{-\infty }^{\infty }W_{x}(t,f)\,dt\end{aligned}}$

Энергетическая собственность

$\int _{-\infty }^{\infty }\int _{-\infty }^{\infty }W_{x}(t,f)\,df\,dt=\int _{-\infty }^{\infty }|x(t)|^{2}\,dt=\int _{-\infty }^{\infty }|X(f)|^{2}\,df$

Восстановление имущества

${\begin{aligned}\int _{-\infty }^{\infty }W_{x}\left({\frac {t}{2}},f\right)e^{i2\pi ft}\,df&=x(t)x^{*}(0)\\\int _{-\infty }^{\infty }W_{x}\left(t,{\frac {f}{2}}\right)e^{i2\pi ft}\,dt&=X(f)X^{*}(0)\end{aligned}}$

Средняя частота условий и среднее время условий

${\begin{aligned}X(f)&=|X(f)|e^{i2\pi \psi (f)},\quad x(t)=|x(t)|e^{i2\pi \phi (t)},\\{\text{if }}\phi '(t)&=|x(t)|^{-2}\int _{-\infty }^{\infty }fW_{x}(t,f)\,df\\{\text{ and }}-\psi '(f)&=|X(f)|^{-2}\int _{-\infty }^{\infty }tW_{x}(t,f)\,dt\end{aligned}}$

Свойства момента

${\begin{aligned}\int _{-\infty }^{\infty }\int _{-\infty }^{\infty }t^{n}W_{x}(t,f)\,dt\,df&=\int _{-\infty }^{\infty }t^{n}|x(t)|^{2}\,dt\\\int _{-\infty }^{\infty }\int _{-\infty }^{\infty }f^{n}W_{x}(t,f)\,dt\,df&=\int _{-\infty }^{\infty }f^{n}|X(f)|^{2}\,df\end{aligned}}$

Недвижимость

$W_{x}^{*}(t,f)=W_{x}(t,f)$

Свойства региона

${\begin{aligned}{\text{If }}x(t)&=0{\text{ for }}t>t_{0}{\text{ then }}W_{x}(t,f)=0{\text{ for }}t>t_{0}\\{\text{If }}x(t)&=0{\text{ for }}t<t_{0}{\text{ then }}W_{x}(t,f)=0{\text{ for }}t<t_{0}\end{aligned}}$

Теорема умножения

${\begin{aligned}{\text{If }}y(t)&=x(t)h(t)\\{\text{then }}W_{y}(t,f)&=\int _{-\infty }^{\infty }W_{x}(t,\rho )W_{h}(t,f-\rho )\,d\rho \end{aligned}}$

Теорема о свертке

${\begin{aligned}{\text{If }}y(t)&=\int _{-\infty }^{\infty }x(t-\tau )h(\tau )\,d\tau \\{\text{then }}W_{y}(t,f)&=\int _{-\infty }^{\infty }W_{x}(\rho ,f)W_{h}(t-\rho ,f)\,d\rho \end{aligned}}$

Теорема корреляции

${\begin{aligned}{\text{If }}y(t)&=\int _{-\infty }^{\infty }x(t+\tau )h^{*}(\tau )\,d\tau {\text{ then }}\\W_{y}(t,\omega )&=\int _{-\infty }^{\infty }W_{x}(\rho ,\omega )W_{h}(-t+\rho ,\omega )\,d\rho \end{aligned}}$

Ковариация со сдвигом во времени

${\begin{aligned}{\text{If }}y(t)&=x(t-t_{0})\\{\text{then }}W_{y}(t,f)&=W_{x}(t-t_{0},f)\end{aligned}}$

Ковариация модуляции

${\begin{aligned}{\text{If }}y(t)&=e^{i2\pi f_{0}t}x(t)\\{\text{then }}W_{y}(t,f)&=W_{x}(t,f-f_{0})\end{aligned}}$

Масштабная ковариация

${\begin{aligned}{\text{If }}y(t)&={\sqrt {a}}x(at){\text{ for some }}a>0{\text{ then }}\\{\text{then }}W_{y}(t,f)&=W_{x}(at,{\frac {f}{a}})\end{aligned}}$

Вигнера

Когда сигнал не ограничен по времени, его функцию распределения Вигнера трудно реализовать. Таким образом, мы добавляем новую функцию (маску) к ее интеграционной части, так что нам нужно реализовать только часть исходной функции вместо того, чтобы интегрировать весь путь от отрицательной бесконечности до положительной бесконечности. Оригинальная функция: $W_{x}(t,f)=\int _{-\infty }^{\infty }x\left(t+{\frac {\tau }{2}}\right)\cdot x^{*}\left(t-{\frac {\tau }{2}}\right)e^{-j2\pi \tau f}\cdot d\tau$ Функция с маской: $W_{x}(t,f)=\int _{-\infty }^{\infty }w(\tau )x\left(t+{\frac {\tau }{2}}\right)\cdot x^{*}\left(t-{\frac {\tau }{2}}\right)e^{-j2\pi \tau f}\cdot d\tau$ $w(\tau )$ является реальным и ограниченным по времени

Реализация

Согласно определению:

${\begin{aligned}W_{x}(t,f)=\int _{-\infty }^{\infty }w(\tau )x\left(t+{\frac {\tau }{2}}\right)\cdot x^{*}\left(t-{\frac {\tau }{2}}\right)e^{-j2\pi \tau f}\cdot d\tau \\W_{x}(t,f)=2\int _{-\infty }^{\infty }w(2\tau ')x\left(t+\tau '\right)\cdot x^{*}\left(t-\tau '\right)e^{-j4\pi \tau 'f}\cdot d\tau '\\W_{x}(n\Delta _{t},m\Delta _{f})=2\sum _{p=-\infty }^{\infty }w(2p\Delta _{t})x((n+p)\Delta _{t})x^{\ast }((n-p)\Delta _{t})e^{-j4\pi mp\Delta _{t}\Delta _{f}}\Delta _{t}\end{aligned}}$

Предположим, что $w(t)=0$ для $|t|>B\rightarrow w(2p\Delta _{t})=0$ для $p<-Q$ и $p>Q$

${\begin{aligned}W_{x}(n\Delta _{t},m\Delta _{f})=2\sum _{p=-Q}^{Q}w(2p\Delta _{t})x((n+p)\Delta _{t})x^{\ast }((n-p)\Delta _{t})e^{-j4\pi mp\Delta _{t}\Delta _{f}}\Delta _{t}\end{aligned}}$

Мы берем $x(t)=\delta (t-t_{1})+\delta (t-t_{2})$ как пример

${\begin{aligned}W_{x}(t,f)=\int _{-\infty }^{\infty }w(\tau )x\left(t+{\frac {\tau }{2}}\right)\cdot x^{*}\left(t-{\frac {\tau }{2}}\right)e^{-j2\pi \tau f}\cdot d\tau \,,\end{aligned}}$

где $w(\tau )$ это реальная функция

А затем мы сравниваем разницу между двумя условиями.

Идеально: $W_{x}(t,f)=0,{\text{ for }}t\neq t_{2},t_{1}$

Когда функция маски $w(\tau )=1$, что означает отсутствие функции маски.

$y(t,\tau )=x(t+{\frac {\tau }{2}})$ $y^{*}(t,-\tau )=x^{*}(t-{\frac {\tau }{2}})$

$W_{x}(t,f)=\int _{-\infty }^{\infty }x(t+{\frac {\tau }{2}})x^{*}(t-{\frac {\tau }{2}})e^{-j2\pi \tau f}d\tau$

$=\int _{-\infty }^{\infty }[\delta (t+{\frac {\tau }{2}}-t_{1})+\delta (t+{\frac {\tau }{2}}-t_{2})][\delta (t-{\frac {\tau }{2}}-t_{1})+\delta (t-{\frac {\tau }{2}}-t_{2})]e^{-j2\pi \tau f}\cdot d\tau$

$=4\int _{-\infty }^{\infty }[\delta (2t+\tau -2t_{1})+\delta (2t+\tau -2t_{2})][\delta (2t-\tau -2t_{1})+\delta (2t-\tau -2t_{2})]e^{j2\pi \tau f}\cdot d\tau$

3 условия

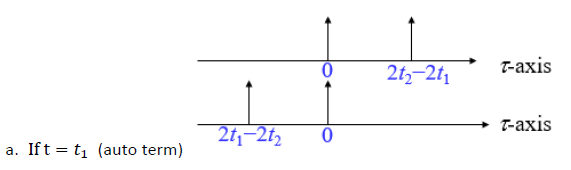
Затем рассмотрим условие с функцией маски:

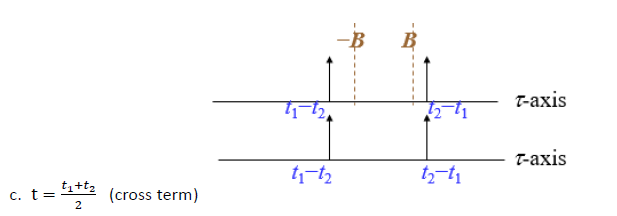
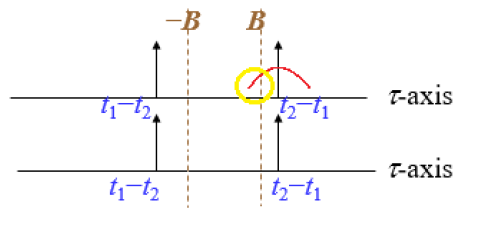
Мы можем видеть это $w(\tau )$ имеют значение только между –B и B, таким образом проводя с $w(\tau )$ можно удалить перекрестный член функции. Но если x(t) не является дельта-функцией или узкочастотной функцией, то вместо этого это функция с широкой частотой или пульсацией. Фронт сигнала все еще может существовать между –B и B, что по-прежнему вызывает проблему перекрестного члена.

например:

См. также

• Частотно-временное представление
• Кратковременное преобразование Фурье
• Спектрограмма
• Преобразование Габора
• Автокорреляция
• Преобразование Габора – Вигнера
• Модифицированная функция распределения Вигнера
• Теорема оптической эквивалентности
• Полиномиальное распределение Вигнера – Вилля
• Функция распределения классов Коэна
• Квазивероятностное распределение Вигнера
• Преобразование между распределениями в частотно-временном анализе
• Билинейное частотно-временное распределение

Дальнейшее чтение

• Вигнер, Э. (1932). «О квантовой поправке к термодинамическому равновесию» (PDF) . Физический обзор . 40 (5): 749–759. Бибкод : 1932PhRv...40..749W . дои : 10.1103/PhysRev.40.749 . hdl : 10338.dmlcz/141466 .
• Ж. Виль , 1948. «Теория и применение концепции аналитического сигнала», Кабели и передача , 2 , 61–74.
• TACM Classen и WFG Mecklenbrauker, 1980. «Распределение Вигнера — инструмент для частотно-временного анализа сигналов; Часть I», Philips J. Res., vol. 35, стр. 217–250.
• Л. Коэн (1989): Proceedings of the IEEE 77, стр. 941–981, Частотно-временные распределения — обзор
• Л. Коэн, Частотно-временной анализ , Прентис-Холл, Нью-Йорк, 1995. ISBN   978-0135945322
• С. Цянь и Д. Чен, Совместный частотно-временной анализ: методы и приложения , гл. 5, Прентис-Холл, Нью-Джерси, 1996 г.
• Б. Боашаш, «Заметка об использовании распределения Вигнера для частотно-временного анализа сигналов», Транзакции IEEE по акустике, речи и обработке сигналов , Vol. 36 , № 9, стр. 1518–1521, сентябрь 1988 г. дои : 10.1109/29.90380 . Б. Боашаш, редактор, Частотно-временной анализ и обработка сигналов – всеобъемлющий справочник , Elsevier Science, Оксфорд, 2003 г., ISBN   0-08-044335-4 .
• Ф. Главач, Г. Ф. Будро-Бартельс : «Линейное и квадратичное частотно-временное представление сигнала», журнал IEEE Signal Processing Magazine, стр. 21–67, апрель 1992 г.
• Р.Л. Аллен и Д.В. Миллс, Анализ сигналов: время, частота, масштаб и структура , Wiley-Interscience, Нью-Джерси, 2004.
• Цзянь-Цзюнь Дин, Конспекты занятий по частотно-временному анализу и вейвлет-преобразованию, факультет электротехники, Национальный тайваньский университет (NTU), Тайбэй, Тайвань, 2015 г.
• Какофенгитис Д. и Стойернагель О. (2017). «Квантовый фазовый пространственный ток Вигнера в слабо ангармонических слабовозбужденных системах с двумя состояниями» European Physical Journal Plus 14.07.2017

Внешние ссылки

• Sonogram Visible Speech под лицензией GPL Бесплатное программное обеспечение для визуального извлечения дистрибутива Wigner.