Оптическое фазовое пространство

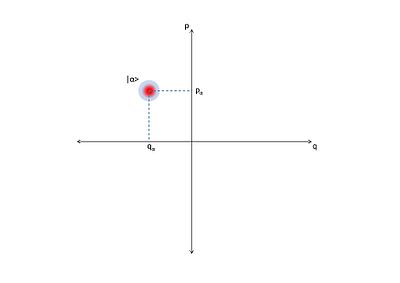
В квантовой оптике оптическое фазовое пространство — это фазовое пространство , в котором все квантовые состояния оптической системы описаны . Каждая точка оптического фазового пространства соответствует уникальному состоянию оптической системы . Для любой такой системы график квадратур друг против друга, возможно, как функции времени, называется фазовой диаграммой . Если квадратуры являются функциями времени, то оптическая фазовая диаграмма может показать эволюцию квантовой оптической системы со временем.

Оптическая фазовая диаграмма может дать представление о свойствах и поведении системы, которые в противном случае могли бы быть неочевидными. Это может указывать на качества системы, которые могут представлять интерес для человека, изучающего оптическую систему, и которые иначе было бы очень трудно сделать. Другое применение оптической фазовой диаграммы состоит в том, что она показывает эволюцию состояния оптической системы. Это можно использовать для определения состояния оптической системы в любой момент времени.

Справочная информация

При обсуждении квантовой теории света очень часто используют электромагнитный осциллятор . в качестве модели ^[1] Электромагнитный осциллятор описывает колебания электрического поля. Поскольку магнитное поле пропорционально скорости изменения электрического поля, оно тоже колеблется. Такие колебания описывают свет. Системы, состоящие из таких генераторов, можно описать оптическим фазовым пространством.

Пусть u ( x ,t) — векторная функция, описывающая одиночную моду электромагнитного генератора . Для простоты предполагается, что этот электромагнитный генератор находится в вакууме. Примером является плоская волна , заданная формулой

\mathbf {u} (\mathbf {x} ,t)=\mathbf {u_{0}} e^{i(\mathbf {k} \cdot \mathbf {x} -\omega t)}

где u0 _, – вектор поляризации k – волновой вектор , $\omega$ частота и А $\cdot$ B обозначает произведение векторов A и B. скалярное Это уравнение плоской волны и является простым примером такого электромагнитного генератора. Исследуемые осцилляторы могут быть либо свободными волнами в пространстве, либо какой-либо нормальной модой, содержащейся в некоторой полости.

Одна мода электромагнитного генератора изолируется от остальной системы и исследуется. Такой осциллятор при квантовании описывается математикой квантового гармонического осциллятора . ^[1] Квантовые осцилляторы описываются с помощью операторов рождения и уничтожения. ${\hat {a}}^{\dagger }$ и ${\hat {a}}$ . Физические величины, такие как напряженность электрического поля , затем становятся квантовыми операторами .

Чтобы отличить физическую величину от квантовомеханического оператора, используемого для ее описания, над символами оператора используется «шляпа». Так, например, где $E_{i}$ может представлять (один из компонентов) электрического поля , символ ${\widehat {E}}_{i}$ обозначает квантовомеханический оператор, описывающий $E_{i}$ . Это соглашение используется на протяжении всей статьи, но не широко используется в более сложных текстах, в которых шляпа избегается, поскольку она просто загромождает текст.

В режиме квантового осциллятора большинство операторов, представляющих физические величины, обычно выражаются через операторы рождения и уничтожения. В этом примере напряженность электрического поля определяется выражением:

{\widehat {E}}_{i}=u_{i}^{*}(\mathbf {x} ,t){\widehat {a}}^{\dagger }+u_{i}(\mathbf {x} ,t){\widehat {a}}

^[2]

(где x _i — отдельный компонент x , позиция). Гамильтониан этого генератора , электромагнитного генератора находится путем квантования электромагнитного поля и формула имеет вид:

{\widehat {H}}=\hbar \omega ({\widehat {a}}^{\dagger }{\widehat {a}}+1/2)

^[2]

где $\omega$ — частота (пространственно-временной) моды. Оператор уничтожения является бозонным оператором уничтожения и поэтому подчиняется каноническому коммутационному соотношению, определяемому формулой:

[{\widehat {a}},{\widehat {a}}^{\dagger }]=1

Собственные состояния оператора уничтожения называются когерентными состояниями :

{\widehat {a}}|\alpha \rangle =\alpha |\alpha \rangle

Важно отметить, что оператор уничтожения не является эрмитовым ; поэтому его собственные значения $\alpha$ может быть сложным. Это имеет важные последствия.

Наконец, номер фотона задается оператором ${\widehat {N}}={\widehat {a}}^{\dagger }{\widehat {a}},$ что дает число фотонов в данной (пространственно-временной) моде u .

Квадратуры

Операторы, заданные

{\widehat {q}}={\tfrac {1}{2}}({\widehat {a}}^{\dagger }+{\widehat {a}})

и

{\widehat {p}}={\tfrac {i}{2}}({\widehat {a}}^{\dagger }-{\widehat {a}})

называются квадратурами и представляют собой действительную и мнимую части комплексной амплитуды, представленной ${\widehat {a}}$ . ^[1] Коммутационное соотношение между двумя квадратурами легко вычислить:

{\begin{aligned}\left[{\widehat {q}},{\widehat {p}}\right]&={\tfrac {i}{4}}[{\widehat {a}}^{\dagger }+{\widehat {a}},{\widehat {a}}^{\dagger }-{\widehat {a}}]\\&={\tfrac {i}{4}}([{\widehat {a}}^{\dagger },{\widehat {a}}^{\dagger }]-[{\widehat {a}}^{\dagger },{\widehat {a}}]+[{\widehat {a}},{\widehat {a}}^{\dagger }]-[{\widehat {a}},{\widehat {a}}])\\&={\tfrac {i}{4}}(-(-1)+1)\\&={\tfrac {i}{2}}\end{aligned}}

Это очень похоже на коммутационное соотношение оператора положения и импульса. Таким образом, может быть полезно думать и рассматривать квадратуры как положение и импульс осциллятора, хотя на самом деле они являются «синфазными и противофазными компонентами амплитуды электрического поля пространственно-временной моды». , или u , и на самом деле не имеют ничего общего с положением или импульсом электромагнитного осциллятора (поскольку трудно определить, что подразумевается под положением и импульсом для электромагнитного осциллятора). ^[1]

Свойства квадратур

Собственные состояния квадратурных операторов ${\widehat {q}}$ и ${\widehat {p}}$ называются квадратурными состояниями. Они удовлетворяют отношениям:

${\widehat {q}}|q\rangle =q|q\rangle$ и ${\widehat {p}}|p\rangle =p|p\rangle$

$\langle q|q'\rangle =\delta (q-q')$ и $\langle p|p'\rangle =\delta (p-p')$

$\int _{-\infty }^{\infty }|q\rangle \langle q|\,dq=1$ и $\int _{-\infty }^{\infty }|p\rangle \langle p|\,dp=1$

поскольку они образуют полные базисные наборы.

Важный результат

Следующее важное соотношение, которое можно вывести из вышесказанного, оправдывает нашу интерпретацию того, что квадратуры являются вещественными и мнимыми частями комплекса. $\alpha$ (т.е. синфазные и противофазные компоненты электромагнитного генератора)

\langle \alpha |{\widehat {q}}|\alpha \rangle ={\frac {1}{2}}(\langle \alpha |{\widehat {a}}^{\dagger }|\alpha \rangle +\langle \alpha |{\widehat {a}}|\alpha \rangle )={\frac {1}{2}}(\alpha ^{*}\langle \alpha |\alpha \rangle +\alpha \langle \alpha |\alpha \rangle )

Ниже приведена зависимость, которую можно использовать для оценки вышесказанного:

\langle \alpha '|\alpha \rangle =e^{(-1/2)(|\alpha '|^{2}+|\alpha |^{2})+\alpha '^{*}\alpha }

^[1]

Это дает нам следующее:

\langle \alpha |{\widehat {q}}|\alpha \rangle ={\frac {1}{2}}(\alpha ^{*}+\alpha )=q_{\alpha }

\langle \alpha |{\widehat {p}}|\alpha \rangle ={\frac {i}{2}}(\alpha ^{*}-\alpha )=p_{\alpha }

способом, аналогичным описанному выше.

\alpha ={\frac {1}{2}}(\langle \alpha |{\widehat {q}}|\alpha \rangle +i\langle \alpha |{\widehat {p}}|\alpha \rangle )={\frac {1}{2}}(q_{\alpha }+ip_{\alpha })

Таким образом, $\alpha$ это просто композиция квадратур.

В этом формализме становится очевидным еще одно очень важное свойство когерентных состояний. Когерентное состояние — это не точка оптического фазового пространства, а распределение на нем. Это можно увидеть через

q_{\alpha }=\langle \alpha |{\widehat {q}}|\alpha \rangle

и

p_{\alpha }=\langle \alpha |{\widehat {p}}|\alpha \rangle

.

Это только ожидаемые значения ${\widehat {q}}$ и ${\widehat {p}}$ для государства $|\alpha \rangle$ .

Можно показать, что квадратуры подчиняются принципу неопределенности Гейзенберга, определяемому следующим образом:

\Delta q\Delta p\geq 1/2

^[1] (где

\Delta q

и

\Delta p

распределений — дисперсии q и p соответственно)

Это неравенство не обязательно должно быть насыщенным, и типичным примером таких состояний являются сжатые когерентные состояния . Когерентные состояния представляют собой гауссовы распределения вероятностей в фазовом пространстве, локализованном вокруг $\alpha$ .

Операторы в фазовом пространстве

Можно определить операторы для перемещения когерентных состояний по фазовому пространству. Они могут создавать новые когерентные состояния и позволят нам перемещаться по фазовому пространству.

Оператор фазового сдвига

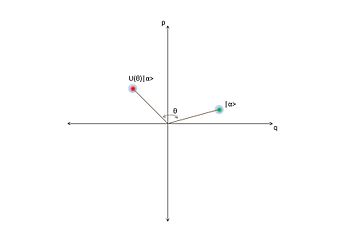
Оператор фазового сдвига поворачивает когерентное состояние на угол $\theta$ в оптическом фазовом пространстве. Этот оператор задается следующим образом:

{\widehat {U}}(\theta )=e^{-\imath \,\theta {\widehat {N}}}

^[1]

где ${\widehat {N}}={\widehat {a}}^{\dagger }{\widehat {a}}$ – числовой оператор рассматриваемой моды излучения.

Важные отношения

{\widehat {U}}(\theta )^{\dagger }{\widehat {a}}{\widehat {U}}(\theta )={\widehat {a}}e^{-i\theta }

выводится следующим образом:

d/d\theta ({\widehat {U}}^{\dagger }{\widehat {a}}{\widehat {U}})=i{\widehat {N}}{\widehat {U}}^{\dagger }{\widehat {a}}{\widehat {U}}-i{\widehat {U}}^{\dagger }{\widehat {a}}{\widehat {U}}{\widehat {N}}={\widehat {U}}^{\dagger }i[{\widehat {N}},{\widehat {a}}]{\widehat {U}}

={\widehat {U}}^{\dagger }i({\widehat {a}}^{\dagger }{\widehat {a}}{\widehat {a}}-{\widehat {a}}{\widehat {a}}^{\dagger }{\widehat {a}}){\widehat {U}}={\widehat {U}}^{\dagger }i[{\widehat {a}}^{\dagger },{\widehat {a}}]{\widehat {a}}{\widehat {U}}=-i{\widehat {U}}^{\dagger }{\widehat {a}}{\widehat {U}}

и решение этого дифференциального уравнения дает желаемый результат.

Таким образом, используя вышеизложенное, становится ясно, что

{\widehat {U}}(\theta )|\alpha \rangle =|\alpha e^{-i\theta }\rangle

,

или поворот на угол тета когерентного состояния в фазовом пространстве. Нижеследующее иллюстрирует это более наглядно:

{\widehat {a}}({\widehat {U}}|\alpha \rangle )={\widehat {U}}{\widehat {a}}e^{-i\theta }|\alpha \rangle

(что получается с учетом того, что фазосдвигающий оператор унитарен

{\widehat {a}}({\widehat {U}}|\alpha \rangle )={\widehat {U}}\alpha e^{-i\theta }|\alpha \rangle =\alpha e^{-i\theta }({\widehat {U}}|\alpha \rangle )

Таким образом,

(\alpha e^{-i\theta },{\widehat {U}}|\alpha \rangle )

является собственной парой

{\widehat {a}}{\widehat {U}}|\alpha \rangle

.

Из этого можно увидеть, что

(\alpha e^{-i\theta }=2^{-1/2}[q_{\alpha }\cos(\theta )+p_{\alpha }\sin(\theta )]+i2^{-1/2}[-q_{\alpha }\sin(\theta )+p_{\alpha }\cos(\theta )],{\widehat {U}}|\alpha \rangle =|\alpha e^{-i\theta }\rangle )

это еще один способ выражения собственной пары, который более четко иллюстрирует влияние оператора фазового сдвига на когерентные состояния.

Оператор смещения

Оператор смещения — это унитарный оператор, который принимает когерентное состояние и переводит его в другое когерентное состояние. Оператор смещения имеет вид

{\widehat {D}}(\alpha )=e^{\alpha {\widehat {a}}^{\dagger }-\alpha ^{*}{\widehat {a}}}

и его название происходит от важного отношения

{\widehat {a}}(\alpha )\equiv {\widehat {D}}^{\dagger }(\alpha ){\widehat {a}}{\widehat {D}}(\alpha )={\widehat {a}}+\alpha

.

Действительно, давайте временно представим ${\widehat {a}}(s)={\widehat {a}}(s\alpha )$ с реальным $s$ и подумай, как ${\widehat {a}}(s)$ меняется, когда $s$ изменяется от 0 до 1. Дифференцирование ${\widehat {a}}(s)$ относительно $s$ , мы находим

${\frac {\partial }{\partial s}}{\widehat {a}}(s)=D^{\dagger }(s\alpha )[\alpha ^{*}{\widehat {a}}-\alpha {\widehat {a}}^{\dagger },{\widehat {a}}]D(s\alpha )=\alpha ,$

так что ${\widehat {a}}(s)={\widehat {a}}(0)+s\alpha .$

Поскольку когерентные состояния являются собственными состояниями как оператора уничтожения, так и оператора умножения на число, легко видеть, что оператор смещения действительно перемещает когерентные состояния, или, точнее,

${\widehat {D}}(\alpha )|\beta \rangle =|\alpha +\beta \rangle .$

Действительно, полученное выше соотношение можно переписать в виде ${\widehat {a}}{\widehat {D}}(\alpha )={\widehat {D}}(\alpha )({\widehat {a}}+\alpha )$ , затем

${\widehat {a}}{\widehat {D}}(\alpha )|\beta \rangle ={\widehat {D}}(\alpha )({\widehat {a}}+\alpha )|\beta \rangle =(\alpha +\beta ){\widehat {D}}(\alpha )|\beta \rangle .$

Таким образом, ${\widehat {D}}(\alpha )|\beta \rangle$ является собственным состоянием оператора уничтожения с собственным значением $\alpha +\beta$ , следовательно ${\widehat {D}}(\alpha )|\beta \rangle =|\alpha +\beta \rangle$ .

В частности,

{\widehat {D}}(-\alpha )|\alpha \rangle =|0\rangle

что приводит к

|\alpha \rangle ={\widehat {D}}(\alpha )|0\rangle

.

Это важно, поскольку показывает, что все когерентные состояния могут быть получены как смещения основного состояния , которое в оптике также является состоянием вакуума .

См. также

Ссылки

^ Jump up to: ^а ^б ^с ^д ^и ^ж ^г Леонхардт, Ульф (2005). Измерение квантового состояния света . Кембридж: Издательство Кембриджского университета . стр. 18–29. ISBN 0-521-02352-1 .
^ Jump up to: ^а ^б Скалли, Марлан; Зубайри, М. Сухайль (1997). Квантовая оптика . Кембридж: Издательство Кембриджского университета . стр. 5 . ISBN 0-521-43595-1 .

[Measuring_the_Quantum_State_of_Light-1] Jump up to: ^а ^б ^с ^д ^и ^ж ^г Леонхардт, Ульф (2005). Измерение квантового состояния света . Кембридж: Издательство Кембриджского университета . стр. 18–29. ISBN 0-521-02352-1 .

[Quantum_Optics-2] Jump up to: ^а ^б Скалли, Марлан; Зубайри, М. Сухайль (1997). Квантовая оптика . Кембридж: Издательство Кембриджского университета . стр. 5 . ISBN 0-521-43595-1 .

[1]

[2]