Кардиоида

Кардиоида

Каустика , появляющаяся на поверхности этой чашки кофе, представляет собой кардиоиду.

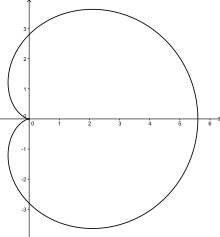
В геометрии кардиоида . (от греч. καρδιά (kardiá) «сердце») — плоская кривая, очерченная точкой на периметре круга, катящегося вокруг неподвижного круга того же радиуса Его также можно определить как эпициклоиду с единственным выступом . Это также разновидность синусоидальной спирали и обратная кривая параболы с фокусом в качестве центра инверсии. Кардиоиду также можно определить как совокупность точек отражения неподвижной точки на окружности через все касательные к окружности.

Кардиоида, создаваемая катящимся кругом по кругу того же радиуса.

Название было придумано Джованни Сальвемини в 1741 году. но кардиоида была предметом изучения десятилетия назад. Хотя он назван в честь своей сердцевидной формы, по форме он больше напоминает очертания круглого яблока без плодоножки.

Кардиоидный микрофон имеет диаграмму направленности акустической характеристики, которая при изображении в двух измерениях напоминает кардиоиду (любая 2D-плоскость, содержащая 3D-прямую линию корпуса микрофона). В трех измерениях кардиоида имеет форму яблока с центром вокруг микрофона, который является «стеблем» яблока.

Уравнения

Генерация кардиоиды и используемая система координат

Позволять $a$ быть общим радиусом двух образующих кругов со средними точками $(-a,0),(a,0)$, $\varphi$ угол прокатки и начало координат (см. рисунок). Человек получает

• параметрическое представление : $${\begin{aligned}x(\varphi )&=2a(1-\cos \varphi )\cdot \cos \varphi \ ,\\y(\varphi )&=2a(1-\cos \varphi )\cdot \sin \varphi \ ,\qquad 0\leq \varphi <2\pi \end{aligned}}$$ и отсюда представление в
• полярные координаты : $$r(\varphi )=2a(1-\cos \varphi ).$$
• Знакомство с заменами $\cos \varphi =x/r$ и ${\textstyle r={\sqrt {x^{2}+y^{2}}}}$ после удаления квадратного корня получаем неявное представление в декартовых координатах : $$\left(x^{2}+y^{2}\right)^{2}+4ax\left(x^{2}+y^{2}\right)-4a^{2}y^{2}=0.$$

Доказательство параметрического представления

Доказательство может быть установлено с использованием комплексных чисел и их общего описания как комплексной плоскости . Перекатывание черного круга по синему можно разделить на два вращения. В комплексной плоскости вращение вокруг точки $0$ (начало координат) под углом $\varphi$ можно выполнить умножением точки $z$ (комплексное число) на $e^{i\varphi }$. Следовательно

вращение $\Phi _{+}$ вокруг точки $a$ является $:z\mapsto a+(z-a)e^{i\varphi }$,

вращение $\Phi _{-}$ вокруг точки $-a$ является: $z\mapsto -a+(z+a)e^{i\varphi }$.

точка $p(\varphi )$ кардиоиды создается путем вращения начала координат вокруг точки $a$ и впоследствии вращаясь вокруг $-a$ под тем же углом $\varphi$: $$p(\varphi )=\Phi _{-}(\Phi _{+}(0))=\Phi _{-}\left(a-ae^{i\varphi }\right)=-a+\left(a-ae^{i\varphi }+a\right)e^{i\varphi }=a\;\left(-e^{i2\varphi }+2e^{i\varphi }-1\right).$$Отсюда получаем параметрическое представление, приведенное выше: $${\begin{array}{cclcccc}x(\varphi )&=&a\;(-\cos(2\varphi )+2\cos \varphi -1)&=&2a(1-\cos \varphi )\cdot \cos \varphi &&\\y(\varphi )&=&a\;(-\sin(2\varphi )+2\sin \varphi )&=&2a(1-\cos \varphi )\cdot \sin \varphi &.&\end{array}}$$( Тригонометрические тождества $e^{i\varphi }=\cos \varphi +i\sin \varphi ,\ (\cos \varphi )^{2}+(\sin \varphi )^{2}=1,$ $\cos(2\varphi )=(\cos \varphi )^{2}-(\sin \varphi )^{2},$ и $\sin(2\varphi )=2\sin \varphi \cos \varphi$ были использованы.)

Метрические свойства

Для кардиоиды, определенной выше, справедливы следующие формулы:

• область $A=6\pi a^{2}$,
• длина дуги $L=16a$ и
• радиус кривизны $\rho (\varphi )={\tfrac {8}{3}}a\sin {\tfrac {\varphi }{2}}\,.$

В доказательствах этих утверждений в обоих случаях используется полярное представление кардиоиды. Подходящие формулы см. в полярной системе координат (длина дуги) и полярной системе координат (площадь).

Доказательство формулы площади

$$A=2\cdot {\tfrac {1}{2}}\int _{0}^{\pi }{(r(\varphi ))^{2}}\;d\varphi =\int _{0}^{\pi }{4a^{2}(1-\cos \varphi )^{2}}\;d\varphi =\cdots =4a^{2}\cdot {\tfrac {3}{2}}\pi =6\pi a^{2}.$$

Доказательство формулы длины дуги

$$L=2\int _{0}^{\pi }{\sqrt {r(\varphi )^{2}+(r'(\varphi ))^{2}}}\;d\varphi =\cdots =8a\int _{0}^{\pi }{\sqrt {{\tfrac {1}{2}}(1-\cos \varphi )}}\;d\varphi =8a\int _{0}^{\pi }\sin \left({\tfrac {\varphi }{2}}\right)d\varphi =16a.$$

Доказательство радиуса кривизны

Радиус кривизны $\rho$ кривой в полярных координатах с уравнением $r=r(\varphi )$ есть (с. кривизна ) $$\rho (\varphi )={\frac {\left[r(\varphi )^{2}+{\dot {r}}(\varphi )^{2}\right]^{3/2}}{r(\varphi )^{2}+2{\dot {r}}(\varphi )^{2}-r(\varphi ){\ddot {r}}(\varphi )}}\ .$$

Для кардиоиды $r(\varphi )=2a(1-\cos \varphi )=4a\sin ^{2}\left({\tfrac {\varphi }{2}}\right)$ каждый получает $$\rho (\varphi )=\cdots ={\frac {\left[16a^{2}\sin ^{2}{\frac {\varphi }{2}}\right]^{\frac {3}{2}}}{24a^{2}\sin ^{2}{\frac {\varphi }{2}}}}={\frac {8}{3}}a\sin {\frac {\varphi }{2}}\ .$$

Характеристики

Аккорды кардиоиды

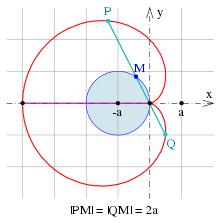
Аккорды через куспид

С1

Хорды, проходящие через вершину кардиоиды, имеют одинаковую длину. $4a$.

С2

Середины , хорд . проходящих через точку возврата, лежат на периметре неподвижной образующей окружности (см. рисунок)

Доказательство C1

Очки $P:p(\varphi ),\;Q:p(\varphi +\pi )$ находятся на аккорде через точку возврата (=начало). Следовательно $${\begin{aligned}|PQ|&=r(\varphi )+r(\varphi +\pi )\\&=2a(1-\cos \varphi )+2a(1-\cos(\varphi +\pi ))=\cdots =4a\end{aligned}}.$$

Доказательство для C2

Для доказательства используется представление в комплексной плоскости (см. выше). Для очков $$P:\ p(\varphi )=a\,\left(-e^{i2\varphi }+2e^{i\varphi }-1\right)$$ и $$Q:\ p(\varphi +\pi )=a\,\left(-e^{i2(\varphi +\pi )}+2e^{i(\varphi +\pi )}-1\right)=a\,\left(-e^{i2\varphi }-2e^{i\varphi }-1\right),$$

середина аккорда $PQ$ является $$M:\ {\tfrac {1}{2}}(p(\varphi )+p(\varphi +\pi ))=\cdots =-a-ae^{i2\varphi }$$ которая лежит на периметре круга со серединой $-a$ и радиус $a$ (см. картинку).

Кардиоида как обратная кривая параболы

Кардиоида, полученная путем инверсии параболы, пересекающей единичную окружность (пунктирная линия).

Основная статья: инверсная геометрия

Кардиоида — это обратная кривая параболы с фокусом в центре инверсии (см. график).

Для примера, показанного на графике, круги генератора имеют радиус ${\textstyle a={\frac {1}{2}}}$. Следовательно, кардиоида имеет полярное представление $$r(\varphi )=1-\cos \varphi$$и ее обратная кривая $$r(\varphi )={\frac {1}{1-\cos \varphi }},$$которая представляет собой параболу (с. парабола в полярных координатах ) с уравнением ${\textstyle x={\tfrac {1}{2}}\left(y^{2}-1\right)}$ в декартовых координатах.

Примечание. Не всякая обратная кривая параболы является кардиоидой. Например, если парабола перевернута по кругу, центр которого лежит в вершине параболы, то результатом будет циссоида Диокла .

Кардиоида как огибающая карандаша кругов

Кардиоида как огибающая карандаша кругов

В предыдущем разделе, если дополнительно инвертировать касательные параболы, можно получить пучок окружностей, проходящий через центр инверсии (начало координат). Детальное рассмотрение показывает: Середины окружностей лежат на периметре неподвижной образующей окружности. (Гообразующая окружность — это обратная кривая директрисы параболы.)

Это свойство приводит к следующему простому методу построения кардиоиды:

1. Выберите круг $c$ и точка $O$ по его периметру,
2. нарисуйте круги, содержащие $O$ с центрами на $c$, и
3. нарисуйте конверт этих кругов.

Доказательство с состоянием конверта

Огибающая карандаша неявно заданных кривых $$F(x,y,t)=0$$ с параметром $t$ состоит из таких точек $(x,y)$ которые являются решениями нелинейной системы $$F(x,y,t)=0,\quad F_{t}(x,y,t)=0,$$ что такое состояние конверта . Обратите внимание, что $F_{t}$ означает частную производную параметра $t$.

Позволять $c$ быть кругом со средней точкой $(-1,0)$ и радиус $1$. Затем $c$ имеет параметрическое представление $(-1+\cos t,\sin t)$. Карандаш кругов с центрами на $c$ содержащая точка $O=(0,0)$ может быть неявно представлено как $$F(x,y,t)=(x+1-\cos t)^{2}+(y-\sin t)^{2}-(2-2\cos t)=0,$$что эквивалентно $$F(x,y,t)=x^{2}+y^{2}+2x\;(1-\cos t)-2y\;\sin t=0\;.$$Второе условие конверта: $$F_{t}(x,y,t)=2x\;\sin t-2y\;\cos t=0.$$Легко проверяется, что точки кардиоиды с параметрическим представлением $$x(t)=2(1-\cos t)\cos t,\quad y(t)=2(1-\cos t)\sin t$$выполнить описанную выше нелинейную систему. Параметр $t$ идентичен параметру угла кардиоиды.

Кардиоида как огибающая карандаша линий

Кардиоида как огибающая карандаша линий

Подобный и простой метод рисования кардиоиды использует карандаш линий . Это принадлежит Л. Кремоне :

1. Нарисуйте круг, разделите его периметр на равные части с помощью $2N$ точки (см. рисунок) и последовательно пронумеруйте их.
2. Нарисуйте аккорды: $(1,2),(2,4),\dots ,(n,2n),\dots ,(N,2N),(N+1,2),(N+2,4),\dots$. (То есть вторая точка перемещается с двойной скоростью.)
3. Огибающая этих аккордов представляет собой кардиоиду.

Поколение кардиоиды Кремоны

Доказательство

В следующем рассмотрении используются тригонометрические формулы для $\cos \alpha +\cos \beta$, $\sin \alpha +\sin \beta$, $1+\cos 2\alpha$, $\cos 2\alpha$, и $\sin 2\alpha$.Для простоты вычислений доказательство приведено для кардиоиды с полярным представлением. $r=2(1\mathbin {\color {red}+} \cos \varphi )$ ( § Кардиоиды в разных положениях ).

Уравнение тангенса кардиоиды = с полярным представлением r 2(1 + cos 𝜑 )

Из параметрического представления $${\begin{aligned}x(\varphi )&=2(1+\cos \varphi )\cos \varphi ,\\y(\varphi )&=2(1+\cos \varphi )\sin \varphi \end{aligned}}$$

получается нормальный вектор ${\vec {n}}=\left({\dot {y}},-{\dot {x}}\right)^{\mathsf {T}}$. Уравнение тангенса ${\dot {y}}(\varphi )\cdot (x-x(\varphi ))-{\dot {x}}(\varphi )\cdot (y-y(\varphi ))=0$ является: $$(\cos 2\varphi +\cos \varphi )\cdot x+(\sin 2\varphi +\sin \varphi )\cdot y=2(1+\cos \varphi )^{2}\,.$$

С помощью тригонометрических формул и последующего деления на ${\textstyle \cos {\frac {1}{2}}\varphi }$, уравнение тангенса можно переписать в виде: $$\cos({\tfrac {3}{2}}\varphi )\cdot x+\sin \left({\tfrac {3}{2}}\varphi \right)\cdot y=4\left(\cos {\tfrac {1}{2}}\varphi \right)^{3}\quad 0<\varphi <2\pi ,\ \varphi \neq \pi .$$

Уравнение хорды окружности 1 , со серединой ( 0 ) и радиусом 3

Для уравнения секущей, проходящей через две точки $(1+3\cos \theta ,3\sin \theta ),\ (1+3\cos {\color {red}2}\theta ,3\sin {\color {red}2}\theta ))$ человек получает: $$(\sin \theta -\sin 2\theta )x+(\cos 2\theta -\sin \theta )y=-2\cos \theta -\sin(2\theta )\,.$$

С помощью тригонометрических формул и последующего деления на ${\textstyle \sin {\frac {1}{2}}\theta }$ уравнение секущей линии можно переписать так: $$\cos \left({\tfrac {3}{2}}\theta \right)\cdot x+\sin \left({\tfrac {3}{2}}\theta \right)\cdot y=4\left(\cos {\tfrac {1}{2}}\theta \right)^{3}\quad 0<\theta <2\pi .$$

Заключение

Несмотря на два угла $\varphi ,\theta$ имеют разные значения (см. картинку), которые можно получить за $\varphi =\theta$ та же линия. Следовательно, любая секущая окружности, определенная выше, также является касательной к кардиоиде:

Кардиоида – это огибающая хорд окружности.

Примечание:
Доказательство можно провести с помощью условий огибающей (см. предыдущий раздел) неявного пучка кривых: $$F(x,y,t)=\cos \left({\tfrac {3}{2}}t\right)x+\sin \left({\tfrac {3}{2}}t\right)y-4\left(\cos {\tfrac {1}{2}}t\right)^{3}=0$$

— карандаш секущих окружности (см. выше) и $$F_{t}(x,y,t)=-{\tfrac {3}{2}}\sin \left({\tfrac {3}{2}}t\right)x+{\tfrac {3}{2}}\cos \left({\tfrac {3}{2}}t\right)y+3\cos \left({\tfrac {1}{2}}t\right)\sin t=0\,.$$

При фиксированном параметре t оба уравнения представляют собой линии. Точкой их пересечения является $$x(t)=2(1+\cos t)\cos t,\quad y(t)=2(1+\cos t)\sin t,$$

которая является точкой кардиоиды с полярным уравнением $r=2(1+\cos t).$

Кардиоида как каустика : источник света $Z$, луч света ${\vec {s}}$, отраженный луч ${\vec {r}}$

Кардиоида в виде каустики круга с источником света (справа) по периметру.

Кардиоида как каустика круга

Соображения, сделанные в предыдущем разделе, дают доказательство того, что каустика круга с источником света на периметре круга является кардиоидой.

Если в плоскости есть источник света в точке $Z$ по периметру круга, отражающего любой луч, то отраженные лучи внутри круга являются касательными кардиоиды.

Доказательство

Как и в предыдущем разделе, круг может иметь середину. $(1,0)$ и радиус $3$. Его параметрическое представление $$c(\varphi )=(1+3\cos \varphi ,3\sin \varphi )\ .$$Касательная в точке окружности $C:\ k(\varphi )$ имеет нормальный вектор ${\vec {n}}_{t}=(\cos \varphi ,\sin \varphi )^{\mathsf {T}}$. Следовательно, отраженный луч имеет вектор нормали ${\vec {n}}_{r}=\left(\cos {\color {red}{\tfrac {3}{2}}}\varphi ,\sin {\color {red}{\tfrac {3}{2}}}\varphi \right)^{\mathsf {T}}$ (см. график) и содержит точку $C:\ (1+3\cos \varphi ,3\sin \varphi )$. Отраженный луч является частью линии с уравнением (см. предыдущий раздел) $$\cos \left({\tfrac {3}{2}}\varphi \right)x+\sin \left({\tfrac {3}{2}}\varphi \right)y=4\left(\cos {\tfrac {1}{2}}\varphi \right)^{3}\,,$$который является касательной кардиоиды с полярным уравнением $$r=2(1+\cos \varphi )$$из предыдущего раздела.

Примечание. При таких рассуждениях обычно пренебрегают многократными отражениями на окружности.

Кардиоида как педальная кривая круга

Точка кардиоиды — это основание опущенного перпендикуляра к касательной окружности.

Поколение кардиоиды Кремоны не следует путать со следующим поколением:

Пусть будет $k$ круг и $O$ точка на периметре этого круга. Верно следующее:

Основания перпендикуляров из точки $O$ по касательным окружности $k$ являются точками кардиоиды.

Следовательно, кардиоида – это особая педальная кривая окружности.

Доказательство

В круге декартовой системы координат $k$ может иметь середину $(2a,0)$ и радиус $2a$. Касательная в точке окружности $(2a+2a\cos \varphi ,2a\sin \varphi )$ имеет уравнение $$(x-2a)\cdot \cos \varphi +y\cdot \sin \varphi =2a\,.$$Основание перпендикуляра из точки $O$ на касательной находится точка $(r\cos \varphi ,r\sin \varphi )$ с еще неизвестной дистанции $r$ к происхождению $O$. Подставляя точку в уравнение касательной, получаем $$(r\cos \varphi -2a)\cos \varphi +r\sin ^{2}\varphi =2a\quad \rightarrow \quad r=2a(1+\cos \varphi )$$что является полярным уравнением кардиоиды.

Примечание: если точка $O$ не находится на периметре круга $k$, получаешь лимасон Паскаля .

Эволюция кардиоиды

  Кардиоида

  Эволюция кардиоиды

  Одна точка Р; его центр кривизны М; и его соприкасающийся круг.

Эволюта . кривой — это место расположения центров кривизны Подробно: Для кривой ${\vec {x}}(s)={\vec {c}}(s)$ с радиусом кривизны $\rho (s)$ Эволюта имеет представление $${\vec {X}}(s)={\vec {c}}(s)+\rho (s){\vec {n}}(s).$$с ${\vec {n}}(s)$ правильно ориентированный блок в норме.

Для кардиоиды получается:

Эволюта . кардиоиды представляет собой другую кардиоиду, размером в одну треть и обращенную в противоположном направлении (рис. рисунок)

Доказательство

Для кардиоиды с параметрическим представлением $$x(\varphi )=2a(1-\cos \varphi )\cos \varphi =4a\sin ^{2}{\tfrac {\varphi }{2}}\cos \varphi \,,$$$$y(\varphi )=2a(1-\cos \varphi )\sin \varphi =4a\sin ^{2}{\tfrac {\varphi }{2}}\sin \varphi$$нормальная единица измерения $${\vec {n}}(\varphi )=(-\sin {\tfrac {3}{2}}\varphi ,\cos {\tfrac {3}{2}}\varphi )$$и радиус кривизны $$\rho (\varphi )={\tfrac {8}{3}}a\sin {\tfrac {\varphi }{2}}\,.$$Следовательно, параметрические уравнения эволюты имеют вид $$X(\varphi )=4a\sin ^{2}{\tfrac {\varphi }{2}}\cos \varphi -{\tfrac {8}{3}}a\sin {\tfrac {\varphi }{2}}\cdot \sin {\tfrac {3}{2}}\varphi =\cdots ={\tfrac {4}{3}}a\cos ^{2}{\tfrac {\varphi }{2}}\cos \varphi -{\tfrac {4}{3}}a\,,$$$$Y(\varphi )=4a\sin ^{2}{\tfrac {\varphi }{2}}\sin \varphi +{\tfrac {8}{3}}a\sin {\tfrac {\varphi }{2}}\cdot \cos {\tfrac {3}{2}}\varphi =\cdots ={\tfrac {4}{3}}a\cos ^{2}{\tfrac {\varphi }{2}}\sin \varphi \,.$$Эти уравнения описывают кардиоиду размером в треть, повернутую на 180 градусов и сдвинутую вдоль оси X на $-{\tfrac {4}{3}}a$.

(Использовались тригонометрические формулы: $\sin {\tfrac {3}{2}}\varphi =\sin {\tfrac {\varphi }{2}}\cos \varphi +\cos {\tfrac {\varphi }{2}}\sin \varphi \ ,\ \cos {\tfrac {3}{2}}\varphi =\cdots ,\ \sin \varphi =2\sin {\tfrac {\varphi }{2}}\cos {\tfrac {\varphi }{2}},\ \cos \varphi =\cdots \ .$)

Ортогональные траектории

Ортогональные кардиоиды

Ортогональная траектория пучка кривых — это кривая, ортогонально пересекающая любую кривую пучка кривых. Для кардиоид верно следующее:

Ортогональные траектории пучка кардиоид с уравнениями $$r=2a(1-\cos \varphi )\ ,\;a>0\ ,\$$ кардиоиды с уравнениями $$r=2b(1+\cos \varphi )\ ,\;b>0\ .$$

(Второй карандаш можно рассматривать как отражение на оси Y первого. См. диаграмму.)

Доказательство

Для кривой, заданной в полярных координатах функцией $r(\varphi )$ имеет место следующая связь с декартовыми координатами: $${\begin{aligned}x(\varphi )&=r(\varphi )\cos \varphi \,,\\y(\varphi )&=r(\varphi )\sin \varphi \end{aligned}}$$

и для производных $${\begin{aligned}{\frac {dx}{d\varphi }}&=r'(\varphi )\cos \varphi -r(\varphi )\sin \varphi \,,\\{\frac {dy}{d\varphi }}&=r'(\varphi )\sin \varphi +r(\varphi )\cos \varphi \,.\end{aligned}}$$

Деление второго уравнения на первое дает декартов наклон касательной к кривой в точке $(r(\varphi ),\varphi )$: $${\frac {dy}{dx}}={\frac {r'(\varphi )\sin \varphi +r(\varphi )\cos \varphi }{r'(\varphi )\cos \varphi -r(\varphi )\sin \varphi }}.$$

Для кардиоид с уравнениями $r=2a(1-\cos \varphi )\;$ и $r=2b(1+\cos \varphi )\$ соответственно получаем: $${\frac {dy_{a}}{dx}}={\frac {\cos(\varphi )-\cos(2\varphi )}{\sin(2\varphi )-\sin(\varphi )}}$$ и $${\frac {dy_{b}}{dx}}=-{\frac {\cos(\varphi )+\cos(2\varphi )}{\sin(2\varphi )+\sin(\varphi )}}\ .$$

(Наклон любой кривой зависит от $\varphi$ только, а не по параметрам $a$ или $b$!)

Следовательно $${\frac {dy_{a}}{dx}}\cdot {\frac {dy_{b}}{dx}}=\cdots =-{\frac {\cos ^{2}\varphi -\cos ^{2}(2\varphi )}{\sin ^{2}(2\varphi )-\sin ^{2}\varphi }}=-{\frac {-1+\cos ^{2}\varphi +1-\cos ^{2}2\varphi }{\sin ^{2}(2\varphi )-\sin ^{2}(\varphi )}}=-1\,.$$Это означает: любая кривая первого пучка ортогонально пересекает любую кривую второго пучка.

4 кардиоиды в полярном представлении и их положение в системе координат

На разных позициях

Выбор других положений кардиоиды в системе координат приводит к другим уравнениям. На картинке показаны 4 наиболее распространенных положения кардиоиды и их полярные уравнения.

В комплексном анализе

Граница центральной области периода 1 множества Мандельброта представляет собой точную кардиоиду.

В комплексном анализе изображение любой окружности , проходящей через начало координат под картой $z\to z^{2}$ является кардиоидой. Одним из применений этого результата является то, что граница центрального компонента периода 1 множества Мандельброта представляет собой кардиоиду, заданную уравнением $$c\,=\,{\frac {1-\left(e^{it}-1\right)^{2}}{4}}.$$

Множество Мандельброта содержит бесконечное количество слегка искаженных копий самого себя, и центральная луковица любой из этих меньших копий представляет собой приблизительную кардиоиду.

Кардиоида, образованная светом на циферблате часов .

Каустики

Некоторые каустики могут иметь форму кардиоид. Катакаустика окружности относительно точки окружности является кардиоидой. Кроме того, катакаустика конуса относительно лучей, параллельных образующей, представляет собой поверхность, сечение которой представляет собой кардиоиду. Это можно увидеть, как на фотографии справа, в конической чашке, частично наполненной жидкостью, когда свет падает издалека и под углом, равным углу конуса. По форме изгиб на дне цилиндрической чашечки представляет собой половину нефроида , который внешне очень похож.

Создание кардиоиды как педальной кривой круга

См. также

• Лимасон
• Нефроид
• Дельтовидная мышца
• жезл Витгенштейна
• Кардиоидный микрофон
• Лемниската Бернулли
• Рамочная антенна
• Радиопеленгатор
• Радиопеленгация
• антенна Яги
• Джованни Сальвемини
• Космическая кардиоида

Ссылки

• Р. К. Йейтс (1952). «Кардиоида». Справочник по кривым и их свойствам . Анн-Арбор, Мичиган: Дж. В. Эдвардс. стр. 4 и след.
• Уэллс Д. (1991). Словарь любопытной и интересной геометрии Penguin . Нью-Йорк: Книги Пингвина. стр. 24–25 . ISBN  0-14-011813-6 .

Внешние ссылки

• «Кардиоида» . Энциклопедия математики . ЭМС Пресс . 2001 [1994].
• О'Коннор, Джон Дж.; Робертсон, Эдмунд Ф. «Кардиоида» . MacTutor Архив истории математики . Университет Сент-Эндрюс .
• Сытный прием кардиоидов в кратчайшие сроки
• Вайсштейн, Эрик В. «Кардиоида» . Математический мир .
• Вайсштейн, Эрик В. «Эпициклоида с 1 острием» . Математический мир .
• Вайсштейн, Эрик В. «Кривая сердца» . Математический мир .
• Кса Ли, Кардиоида (1998) (На этом сайте представлен ряд альтернативных конструкций) .
• Ян Вассенаар, Кардиоида , (2005)