Итерация с фиксированной точкой

В численном анализе итерация с фиксированной точкой — это метод вычисления фиксированных точек функции.

Более конкретно, если задана функция $f$ определяется действительными числами с действительными значениями и заданной точкой $x_{0}$ в области $f$ , итерация с фиксированной точкой $x_{n+1}=f(x_{n}),\,n=0,1,2,\dots$ что приводит к последовательности $x_{0},x_{1},x_{2},\dots$ приложений повторяющимися функциями с $x_{0},f(x_{0}),f(f(x_{0})),\dots$ который, как надеются, сойдется к точке $x_{\text{fix}}$ . Если $f$ непрерывна, то можно доказать, что полученное $x_{\text{fix}}$ является фиксированной точкой $f$ , то есть, $f(x_{\text{fix}})=x_{\text{fix}}.$

В более общем смысле функция $f$ может быть определен в любом метрическом пространстве со значениями в этом же пространстве.

Примеры

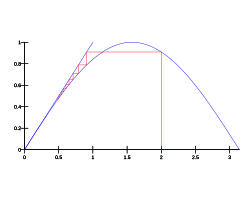
Первым простым и полезным примером является вавилонский метод вычисления квадратного корня из $a > 0$ , который заключается в взятии $f(x)={\frac {1}{2}}\left({\frac {a}{x}}+x\right)$ , то есть среднее значение $x$ и $a / x$ , чтобы приблизиться к пределу $x={\sqrt {a}}$ (из любой отправной точки $x_{0}\gg 0$ ). Это частный случай метода Ньютона, приведенного ниже.
Итерация с фиксированной точкой $x_{n+1}=\cos x_{n}\,$ сходится к единственной неподвижной точке функции $f(x)=\cos x\,$ для любой отправной точки $x_{0}.$ Этот пример действительно удовлетворяет (самое позднее после первого шага итерации) предположениям банаховой теоремы о неподвижной точке . Следовательно, ошибка после n шагов удовлетворяет условиям $|x_{n}-x|\leq {q^{n} \over 1-q}|x_{1}-x_{0}|=Cq^{n}$ (где мы можем взять $q=0.85$ , если мы начнем с $x_{0}=1$ .) Когда ошибка меньше кратного $q^{n}$ для некоторой постоянной $q$ мы говорим, что имеем линейную сходимость . Теорема Банаха о неподвижной точке позволяет получать итерации с неподвижной точкой с линейной сходимостью.
Требование $непрерывности f$ важно, как показывает следующий пример. Итерация $x_{n+1}={\begin{cases}{\frac {x_{n}}{2}},&x_{n}\neq 0\\1,&x_{n}=0\end{cases}}$ сходится к 0 для всех значений $x_{0}$ . Однако 0 не является фиксированной точкой функции $f(x)={\begin{cases}{\frac {x}{2}},&x\neq 0\\1,&x=0\end{cases}}$ поскольку эта функция не является непрерывной при $x=0$ , и фактически не имеет неподвижных точек.

Привлечение фиксированных точек

Притягивающая неподвижная точка функции $f$ — это фиксированная точка $x fix$ функции $f$ с окрестностью $U$ «достаточно близких» точек вокруг $x fix,$ такая, что для любого значения $x$ в $U$ последовательность итераций с фиксированной точкой $x,\ f(x),\ f(f(x)),\ f(f(f(x))),\dots$ содержится в $U$ и сходится к $x fix$ . Бассейн притяжения $x fix$ является крупнейшей такой окрестностью $U$ . ^[1]

Функция натурального косинуса («естественный» означает радианы , а не градусы или другие единицы измерения) имеет ровно одну фиксированную точку, и эта фиксированная точка притягивает. В этом случае «достаточно близко» вообще не является строгим критерием — чтобы продемонстрировать это, начните с любого действительного числа и несколько раз нажмите клавишу cos на калькуляторе (сначала проверив, что калькулятор находится в режиме «радианы»). В конечном итоге оно сходится к числу Дотти (около 0,739085133), которое является фиксированной точкой. Именно здесь график косинуса пересекает линию $y=x$ . ^[2]

Не все фиксированные точки притягиваются. Например, 0 — это фиксированная точка функции $f (x) = 2 x$ , но итерация этой функции для любого значения, отличного от нуля, быстро расходится. Мы говорим, что фиксированная точка $f(x)=2x$ отталкивает.

Притягивающая неподвижная точка называется устойчивой неподвижной точкой, если она также устойчива по Ляпунову .

Неподвижная точка называется нейтрально-устойчивой, если она устойчива по Ляпунову , но не притягивает. Центр линейного однородного дифференциального уравнения второго порядка является примером нейтрально-устойчивой неподвижной точки.

Несколько притягивающих точек могут быть собраны в притягивающий фиксированный набор .

Банахова теорема о неподвижной точке

Теорема Банаха о неподвижной точке дает достаточное условие существования притягивающих неподвижных точек. Функция сокращения отображения $f$ определенное в полном метрическом пространстве, имеет ровно одну фиксированную точку, и итерация с фиксированной точкой притягивается к этой фиксированной точке для любого начального предположения. $x_{0}$ в области определения функции. Распространенными особыми случаями являются следующие: (1) $f$ определяется на вещественной прямой с действительными значениями и является непрерывным по Липшицу с константой Липшица $L<1$ , и (2) функция $f$ непрерывно дифференцируема в открытой окрестности неподвижной точки $x fix$ , и $|f'(x_{\text{fix}})|<1$ .

Хотя существуют и другие теоремы о неподвижных точках , эта особенно полезна, поскольку не все неподвижные точки привлекательны. При построении итерации с фиксированной точкой очень важно убедиться, что она сходится к фиксированной точке. Обычно мы можем использовать теорему Банаха о неподвижной точке, чтобы показать, что неподвижная точка притягивает.

Аттракторы

Привлечение неподвижных точек является частным случаем более широкой математической концепции аттракторов . Итерации с фиксированной точкой представляют собой дискретную динамическую систему с одной переменной. Теория бифуркаций изучает динамические системы и классифицирует различные поведения, такие как притяжение неподвижных точек, периодические орбиты или странные аттракторы . Примером системы является логистическая карта .

Итерационные методы

В вычислительной математике итерационный метод — это математическая процедура, использующая начальное значение для генерации последовательности улучшения приближенных решений класса задач, в которой n-е приближение выводится из предыдущих. Сходящиеся итерации с фиксированной точкой представляют собой математически строгую формализацию итерационных методов.

Примеры итерационного метода

Метод Ньютона — это алгоритм поиска корней заданной дифференцируемой функции ⁠ $f(x)$ ⁠ . Итерация ${\textstyle x_{n+1}=x_{n}-{\frac {f(x_{n})}{f'(x_{n})}}.}$
Если мы напишем ${\textstyle g(x)=x-{\frac {f(x)}{f'(x)}}}$ , мы можем переписать итерацию Ньютона как итерацию с фиксированной точкой ${\textstyle x_{n+1}=g(x_{n})}$ .
Если эта итерация сходится к фиксированной точке $x_{\text{fix}}$ г $тогда$ , ${\textstyle x_{\text{fix}}=g(x_{\text{fix}})=x_{\text{fix}}-{\frac {f(x_{\text{fix}})}{f'(x_{\text{fix}})}}}$ , так ${\textstyle f(x_{\text{fix}})/f'(x_{\text{fix}})=0,}$
поэтому $f(x_{\text{fix}})=0$ , то есть, $x_{\text{fix}}$ является корнем $f$ . В предположениях банаховой теоремы о неподвижной точке итерация Ньютона, оформленная как метод неподвижной точки, демонстрирует линейную сходимость . Однако более детальный анализ показывает квадратичную сходимость , т.е. ${\textstyle |x_{n}-x_{\text{fix}}|<Cq^{2^{n}}}$ , при определенных обстоятельствах.
Метод Галлея аналогичен методу Ньютона , если он работает правильно, но его ошибка заключается в $|x_{n}-x_{\text{fix}}|<Cq^{3^{n}}$ ( кубическая сходимость ). В общем, можно разработать методы, которые сходятся со скоростью $Cq^{k^{n}}$ для любого $k\in \mathbb {N}$ . Как правило, чем выше $k$ , тем оно менее стабильно и тем дороже оно становится в вычислительном отношении. По этим причинам методы более высокого порядка обычно не используются.
Методы Рунге-Кутты и численные средства решения обыкновенных дифференциальных уравнений в целом можно рассматривать как итерации с фиксированной точкой. Действительно, основная идея при анализе A-стабильности решателей ОДУ состоит в том, чтобы начать с особого случая. $y'=ay$ , где $a$ — комплексное число , и проверить, сходится ли решатель ОДУ к фиксированной точке $y_{\text{fix}}=0$ всякий раз, когда реальная часть $a$ является отрицательным. ^[а]
Теорема Пикара -Линделефа , показывающая, что обыкновенные дифференциальные уравнения имеют решения, по сути представляет собой применение теоремы Банаха о неподвижной точке к специальной последовательности функций, которая образует итерацию с неподвижной точкой, создавая решение уравнения. Решение ОДУ таким способом называется итерацией Пикара , методом Пикара или итерационным процессом Пикара .
Возможности итерации в Excel можно использовать для поиска решений уравнения Колбрука с точностью до 15 значащих цифр. ^[3]^[4]
Некоторые из схем «последовательного приближения», используемых в динамическом программировании для решения функционального уравнения Беллмана, основаны на итерациях с фиксированной точкой в пространстве возвращаемой функции. ^[5]^[6]
Паутинная модель теории цен соответствует итерации с фиксированной точкой состава функции предложения и функции спроса. ^[7]

Ускорение сходимости

Скорость сходимости итерационной последовательности можно увеличить, используя метод ускорения сходимости, такой как ускорение Андерсона и процесс Эйткена с дельта-квадратом . Применение метода Эйткена к итерации с фиксированной точкой известно как метод Стеффенсена , и можно показать, что метод Стеффенсена дает скорость сходимости, которая является по крайней мере квадратичной.

Игра Хаос

Термин «игра хаоса» относится к методу создания фиксированной точки любой системы итерированных функций (IFS). Начиная с любой точки $x 0$ , последовательные итерации формируются как $x k +1 = f r (x k)$ , где $f r$ — член заданной IFS, случайно выбираемый для каждой итерации. Следовательно, игра хаоса представляет собой рандомизированную итерацию с фиксированной точкой. Игра хаоса позволяет построить общую форму фрактала , такого как треугольник Серпинского , повторяя итерационный процесс большое количество раз. С математической точки зрения итерации сходятся к фиксированной точке IFS. Всякий раз, когда $x 0$ принадлежит аттрактору IFS, все итерации $x k$ остаются внутри аттрактора и с вероятностью 1 образуют плотное множество в последнем .

См. также

Ссылки

^ Можно также считать определенные итерации A-стабильными, если итерации остаются ограниченными в течение длительного времени, что выходит за рамки этой статьи.

^ Рассиас, Фемистокл М.; Пардалос, Панос М. (17 сентября 2014 г.). Математика без границ: Обзоры по чистой математике . Спрингер. ISBN 978-1-4939-1106-6 .
^ Вайсштейн, Эрик В. «Число Дотти» . Вольфрам Математический мир . Вольфрам Рисерч, Инк . Проверено 23 июля 2016 г.
^ М. А. Кумар (2010), Решение неявных уравнений (Коулбрук) на рабочем листе, Createspace, ISBN 1-4528-1619-0
^ Бркич, Деян (2017) Решение неявного уравнения Колбрука для трения потока с использованием Excel, Электронные таблицы в образовании (eJSiE): Vol. 10: Вып. 2, статья 2. Доступно по адресу: https://sie.scholasticahq.com/article/4663-solution-of-the-implicit-colebrook-equation-for-flow-friction-using-excel.
^ Беллман, Р. (1957). Динамическое программирование, Издательство Принстонского университета.
^ Снедович, М. (2010). Динамическое программирование: основы и принципы, Тейлор и Фрэнсис .
^ Онодзаки, Тамоцу (2018). «Глава 2. Одномерная нелинейная паутинная модель». Нелинейность, ограниченная рациональность и неоднородность: некоторые аспекты рыночной экономики как сложных систем . Спрингер. ISBN 978-4-431-54971-0 .

Дальнейшее чтение

Берден, Ричард Л.; Фейрес, Дж. Дуглас (1985). «Итерация с фиксированной точкой». Численный анализ (Третье изд.). Издательство ПВС. ISBN 0-87150-857-5 .
Хоффман, Джо Д.; Франкель, Стивен (2001). «Итерация с фиксированной точкой» . Численные методы для инженеров и ученых (второе изд.). Нью-Йорк: CRC Press. стр. 141–145. ISBN 0-8247-0443-6 .
Джадд, Кеннет Л. (1998). «Итерация с фиксированной точкой» . Численные методы в экономике . Кембридж: MIT Press. стр. 165–167. ISBN 0-262-10071-1 .
Штернберг, Шломо (2010). «Итерация и фиксированные точки». Динамические системы (Первое изд.). Дуврские публикации. ISBN 978-0486477053 .
Шашкин, Юрий А. (1991). «9. Итерационный метод». Фиксированные точки (Первое изд.). Американское математическое общество. ISBN 0-8218-9000-Х .
Роза, Алессандро (2021). «Эпизодическая история ступенчатой итерационной диаграммы» . Антикварные Mathematicae . 15 :3–90. дои : 10.14708/am.v15i1.7056 . S2CID 247259939 .

Внешние ссылки

[3] Можно также считать определенные итерации A-стабильными, если итерации остаются ограниченными в течение длительного времени, что выходит за рамки этой статьи.

[1] Рассиас, Фемистокл М.; Пардалос, Панос М. (17 сентября 2014 г.). Математика без границ: Обзоры по чистой математике . Спрингер. ISBN 978-1-4939-1106-6 .

[wolfram-2] Вайсштейн, Эрик В. «Число Дотти» . Вольфрам Математический мир . Вольфрам Рисерч, Инк . Проверено 23 июля 2016 г.

[4] М. А. Кумар (2010), Решение неявных уравнений (Коулбрук) на рабочем листе, Createspace, ISBN 1-4528-1619-0

[5] Бркич, Деян (2017) Решение неявного уравнения Колбрука для трения потока с использованием Excel, Электронные таблицы в образовании (eJSiE): Vol. 10: Вып. 2, статья 2. Доступно по адресу: https://sie.scholasticahq.com/article/4663-solution-of-the-implicit-colebrook-equation-for-flow-friction-using-excel.

[6] Беллман, Р. (1957). Динамическое программирование, Издательство Принстонского университета.

[7] Снедович, М. (2010). Динамическое программирование: основы и принципы, Тейлор и Фрэнсис .

[8] Онодзаки, Тамоцу (2018). «Глава 2. Одномерная нелинейная паутинная модель». Нелинейность, ограниченная рациональность и неоднородность: некоторые аспекты рыночной экономики как сложных систем . Спрингер. ISBN 978-4-431-54971-0 .

[1]

[2]

[а]

[3]

[4]

[5]

[6]

[7]

v т и Алгоритмы поиска корня
Брекетинг (без производной)	Метод бисекции Подделки правил метод ИТП
Домохозяин	метод Ньютона метод Галлея
Квазиньютон	метод Бройдена Метод секущего метод Стеффенсена
Гибридные методы	метод Брента Метод рыцарей
Полиномиальные методы	Жертва не удалась Метод Бэрстоу Метод Дюрана – Кернера метод Греффе Алгоритм Дженкинса – Трауба Алгоритм Лемера – Шура метод Лагерра Метод расщепления круга
Другие методы	Итерация с фиксированной точкой Обратная квадратичная интерполяция метод Мюллера Обобщенный метод секущих Сиди