Контакт (математика)
В математике две функции имеют контакт порядка k , если в точке P они имеют одинаковое значение и их первые k производные равны. Это отношение эквивалентности , классы эквивалентности которого обычно называют струями . Точку соприкосновения также называют двойным бугорком . Контакт — это геометрическое понятие; его можно определить алгебраически как оценку .
Говорят также о кривых и геометрических объектах, имеющих контакт k -го порядка в точке: это также называется соприкосновением (т.е. целованием), обобщая свойство касания . (Здесь производные рассматриваются по длине дуги.) Соприкасающаяся кривая из данного семейства кривых - это кривая, которая имеет наивысший возможный порядок контакта с данной кривой в данной точке; например, касательная линия представляет собой соприкасающуюся кривую из семейства прямых и имеет контакт первого порядка с данной кривой; соприкасающийся круг — это соприкасающаяся кривая из семейства окружностей , имеющая контакт второго порядка (тот же касательный угол и кривизна) и т. д. [1]
Приложения [ править ]
Контактные формы — это частные дифференциальные формы степени 1 на нечетномерных многообразиях; см. геометрию контакта . Контактные преобразования — это связанные изменения координат, имеющие важное значение в классической механике . См. также Преобразование Лежандра .
Контакт между многообразиями часто изучается в теории особенностей , где классифицируются типы контакта, к ним относятся серия A ( A 0 : пересечение, A 1 : касательная, A 2 : соприкасающаяся, ...) и пуповинная или D -серия. где имеется высокая степень контакта со сферой.
Контакт между кривыми [ править ]
две кривые на плоскости, пересекающиеся в точке p, Говорят, что имеют:
- Контакт 0-го порядка, если кривые имеют простое пересечение (не касательную).
- Контакт 1-го порядка, если две кривые касаются .
- Контакт 2-го порядка, если кривизны кривых равны. Такие кривые называются соприкасающимися.
- Контакт 3-го порядка, если производные кривизны равны.
- Контакт 4-го порядка, если вторые производные кривизны равны.
Контакт между кривой и кругом [ править ]
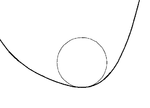

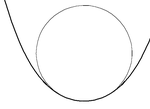
Для каждой точки S ( t ) на гладкой плоской кривой S существует ровно один соприкасающийся круг , радиус которого является обратной величиной κ( t ), кривизны S в точке t . Если кривизна равна нулю (в точке перегиба кривой), соприкасающаяся окружность представляет собой прямую линию. Место расположения центров всех соприкасающихся окружностей (также называемых «центрами кривизны») является эволютой кривой.
Если производная кривизны κ'( t ) равна нулю, то соприкасающаяся окружность будет иметь контакт третьего порядка, и говорят, что кривая имеет вершину . Эволюта будет иметь точку возврата в центре круга. Знак второй производной кривизны определяет, имеет ли кривая локальный минимум или максимум кривизны. Все замкнутые кривые будут иметь не менее четырех вершин, двух минимумов и двух максимумов ( теорема о четырех вершинах ).
В общем случае кривая не будет иметь контакта 4-го порядка с какой-либо окружностью. Однако контакт 4-го порядка может происходить в общем случае в однопараметрическом семействе кривых, на кривой в семействе, где (при изменении параметра) две вершины (одна максимальная и одна минимальная) сходятся вместе и аннигилируют. В таких точках вторая производная кривизны будет равна нулю.
C-окружности, которые имеют двухточечный контакт с двумя точками S ( t 1 ), S ( t 2 ) на кривой, являются двукасательными окружностями. Центры всех двукасательных окружностей образуют множество симметрии . является Медиальная ось подмножеством набора симметрии.
Ссылки [ править ]
- ^ Раттер, JW (2000), Геометрия кривых , CRC Press, стр. 174–175, ISBN 9781584881667 .
- Брюс, JW; П. Дж. Гиблин (1992). Кривые и особенности . Кембридж. ISBN 0-521-42999-4 .
- Ян Р. Портеус (2001) Геометрическое дифференцирование , стр. 152–7, Cambridge University Press ISBN 0-521-00264-8 .