Конечный штат Машина

Классы автоматов

(Нажатие на каждый слой получает статью на эту тему)

Конечный автомат ( FSM ) или конечный автомат ( FSA , множественное число: Automata ), конечный автомат или просто состояние состояния , является математической моделью вычислений . Это абстрактная машина , которая может быть точно в одном из конечных состояний в любой момент времени. FSM может перейти от одного состояния на другое в ответ на некоторые входы ; Переход от одного состояния в другое называется переходом . ^{[ 1 ]} FSM определяется списком его состояний, его начальным состоянием и входами, которые запускают каждый переход. Конечные машины составляют два типа- детерминированные машины с конечным состоянием и неэнергинистические машины конечных состояний . ^{[ 2 ]} Для любой нетерминированной машины конечного состояния можно построить эквивалентный детерминированный.

Поведение государственных машин можно наблюдать во многих устройствах в современном обществе, которые выполняют заранее определенную последовательность действий в зависимости от последовательности событий, с которыми они представлены. Простыми примерами являются: торговые автоматы , которые распределяют продукты, когда наносится надлежащая комбинация монет; Лифты , чья последовательность остановок определяется полами, запрашиваемыми гонщиками; светофоры , которые изменяют последовательность, когда автомобили ждут; комбинированные блокировки , которые требуют ввода последовательности чисел в правильном порядке.

Конечная машина имеет меньшую вычислительную мощность, чем некоторые другие модели вычислений, такие как машина Тьюринга . ^{[ 3 ]} Вычислительное различие мощности означает, что существуют вычислительные задачи, которые может выполнять машина Тьюринга, но FSM не может. FSM Это связано с тем, что память ограничена количеством состояний, которые она имеет. Конечный штат машина обладает той же вычислительной мощностью, что и машина Тьюринга, которая ограничена таким образом, что его голова может выполнять только операции «чтение», и всегда должна двигаться слева направо. FSM изучаются в более общей области теории автоматов .

Пример: монета

Примером простого механизма, который может быть смоделирован государственной машиной, является турникетом . ^{[ 4 ]}^{[ 5 ]} Туринка, используемый для контроля доступа к метро и аттракциону парка развлечений, представляют собой ворота с тремя вращающимися руками на высоте талии, по одному по всему входу. Первоначально руки заблокированы, блокируя вход, не позволяя посетителям проходить через. Депонирование монеты или токена в слот на турникете открывает руки, позволяя одному клиенту протолкнуть. После того, как клиент пройдет через, руки снова заблокируются, пока не вставлена другая монета.

Рассматриваемая как государственная машина, турникета имеет два возможных состояния: заблокированные и разблокированные . ^{[ 4 ]} Есть два возможных входа, которые влияют на его состояние: положить монету в слот ( монета ) и толкать руку ( толчок ). В заблокированном состоянии нажатие на руку не имеет никакого эффекта; Независимо от того, сколько раз входной толчок дается , он остается в заблокированном состоянии. Вкладывая монету - то есть придает машине вход монеты - смещает состояние с заблокированного в разблокированное . В разблокированном состоянии, внедрение дополнительных монет не имеет никакого эффекта; То есть предоставление дополнительных входов монет не меняет состояние. Клиент, проталкивающий руки, дает ввод толчков и сбрасывает состояние заблокированного .

Машина состояния турникета может быть представлена таблицей трансляции состояний , показывающая для каждого возможного состояния переходы между ними (на основе входов, приведенных машине) и выходов, полученных от каждого входа:

Текущее состояние	Вход	Следующее состояние	Выход
Заперт	монета	Разблокирован	Разблокирует турнику, чтобы клиент мог протолкнуться.
Заперт	толкать	Заперт	Никто
Разблокирован	монета	Разблокирован	Никто
Разблокирован	толкать	Заперт	Когда клиент протолкнулся, блокирует турнику.

Машина состояния турникета также может быть представлена направленным графом, называемым диаграммой состояния (выше) . Каждое состояние представлено узлом ( круг ) . Крайки ( стрелки ) показывают переходы от одного штата в другое. Каждая стрелка помечена входом, который запускает этот переход. Вход, который не вызывает изменения состояния (например, входной монеты в разблокированном состоянии), представлен круговой стрелкой, возвращающейся в исходное состояние. Стрелка в заблокированный узел из черной точки указывает, что это начальное состояние.

Концепции и терминология

Состояние - это описание статуса системы, которая ждет, чтобы выполнить переход . Переход - это набор действий, которые будут выполнены, когда условие выполняется или когда событие получено. Например, при использовании аудиосистемы для прослушивания радио (система находится в состоянии «радио»), получение «следующего» стимула приводит к переходу на следующую станцию. Когда система находится в состоянии «CD», стимул «следующий» приводит к переходу на следующий трек. Идентичные стимулы вызывают различные действия в зависимости от текущего состояния.

В некоторых представлениях машин с конечным состоянием также можно связать действия с состоянием:

an entry action: performed when entering the state, and
Выходное действие: выполняется при выходе из состояния.

Представления

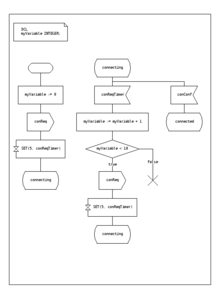
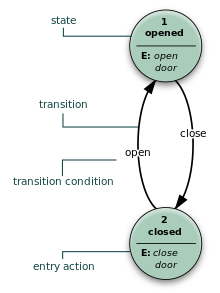
Таблица состояния/события

несколько типов таблиц транспорта штатов Используются . Наиболее распространенное представление показано ниже: комбинация текущего состояния (например, B) и входного (например, Y) показывает следующее состояние (например, C). Информация о полном действии не описана напрямую в таблице и может быть добавлена только с помощью сноски. ^{[ необходимо дальнейшее объяснение ]} Определение FSM, включающее информацию полного действия, возможно с использованием таблиц состояния (см. Также виртуальную машину конечного состояния ).

Таблица трансляции государства
Текущий состояние Вход	Государство а	Государство б	Состояние c
Ввод X.	...	...	...
Ввод Y.	...	Состояние c	...
Вход Z.	...	...	...

Умл Государственные машины

У единого языка моделирования есть обозначение для описания государственных машин. Государственные машины UML преодолевают ограничения ^{[ Цитация необходима ]} традиционных конечных штатных машин, сохраняя при этом свои основные преимущества. Государственные машины UML вводят новые концепции иерархически вложенных государств и ортогональных регионов , одновременно расширяя понятие действий . У UML State Machines имеют характеристики как Mealy Machines , так и Moore Machines . Они поддерживают действия, которые зависят как от состояния системы, так и от запускающегося события , как и в Mealy Machines, а также на действиях въезда и выхода , которые связаны с состояниями, а не с переходами, как в машинах Мура. ^{[ Цитация необходима ]}

Государственные машины SDL

Язык спецификации и описания является стандартом из МСП , который включает в себя графические символы для описания действий в переходе:

Отправить мероприятие
получить мероприятие
Начните таймер
Отменить таймер
Начните еще одну одновременную государственную машину
решение

SDL внедряет основные типы данных, называемые «абстрактными типами данных», языком действий и семантикой выполнения, чтобы сделать исполняемый файл конечного состояния. ^{[ Цитация необходима ]}

Другие диаграммы состояния

Существует большое количество вариантов, чтобы представлять FSM, такой как на рисунке 3.

Использование

В дополнение к их использованию в моделировании реактивных систем, представленных здесь, машины конечных состояний являются значительными во многих различных областях, включая электротехника , лингвистику , информатику , философию , биологию , математику , программирование видеоигр и логику . Конечные машины-это класс автоматов, изученных в теории автоматов и теории вычислений . В области компьютерных наук машины конечных состояний широко используются при моделировании поведения приложений ( теория управления ), проектирование аппаратных цифровых систем , разработки программного обеспечения , компиляторов , сетевых протоколов и вычислительной лингвистики .

Классификация

Машины с конечным состоянием могут быть разделены на акцепторы, классификаторы, преобразователи и секвенсоры. ^{[ 6 ]}

Акцепторы

Рис. 5: Представление акцептора; В этом примере показан один, который определяет, имеет ли двоичное число равномерное число 0, где S ₁ является *приемлемым состоянием* , а S ₂ - это *не принимающее состояние* .

Акцепторы (также называемые детекторами или распознавателями ) производят двоичный выход, указывая, принимается ли принятый вход. Каждое состояние акцептора либо принимает , либо не принимает . Как только весь ввод был получен, если текущее состояние является состоянием принятия, вход принимается; в противном случае это отвергается. Как правило, ввод - это последовательность символов (символы); Действия не используются. Начальное состояние также может быть принятым состоянием, и в этом случае акцептор принимает пустую строку. На примере на рисунке 4 показан акцептор, который принимает строку «NICE». В этом акцепторе единственным приемлемым государством является государство 7.

(Возможно, бесконечный) набор последовательностей символов, называемый формальным языком , является обычным языком, если есть какой -то акцептор, который точно принимает этот набор. Например, набор двоичных строк с равномерным количеством нулей является обычным языком (ср. Рис. 5), в то время как набор всех строк, длина которых является основным числом. ^{[ 7 ]}^: 18, 71

Согласитель также может быть описан как определение языка, который будет содержать каждую строку, принятую акцептором, но ни один из отвергнутых; Этот язык принимается акцептором. По определению, языки, принятые акцепторами, являются обычными языками .

Проблема определения языка, принятого данным акцептором, является экземпляром проблемы алгебраического пути - его обобщение самой короткой проблемы пути к графикам с ребрами, взвешенными элементами (произвольной) полужига . ^{[ 8 ]}^{[ 9 ]}^{[ жаргон ]}

Пример принятия состояния появляется на рис. 5: Детерминированный конечный автомат (DFA), который обнаруживает, содержит ли бинарная входная строка более равномерное число 0s.

S ₁ (которое также является начальным состоянием) указывает на состояние, в котором было входно, что равномерное число 0s. Следовательно, S ₁ является принятым состоянием. Этот акцептор закончится в состоянии приема, если двоичная строка содержит равномерное количество 0s (включая любую двоичную строку, содержащую № 0s). Примерами строк, принятых этим акцептором, являются ε ( пустая строка ), 1, 11, 11 ..., 00, 010, 1010, 10110 и т. Д.

Классификаторы

Классификаторы являются обобщением акцепторов, которые производят n -ary enwertion, где n строго больше, чем два. ^{[ 10 ]}

Преобразователи

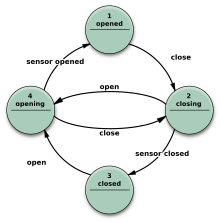
Преобразователи производят выход на основе данного входного и/или состояния, использующего действия. Они используются для управляющих приложений и в области вычислительной лингвистики .

В приложениях управления два типа отличаются:

Мур Машина: FSM использует только действия входа, т.е. вывод зависит только от состояния. Преимущество модели Мура - упрощение поведения. Рассмотрим дверь лифта. Машина состояния распознает две команды: «command_open» и «command_close», которые запускают состояние состояния. Входное действие (e :) в состоянии «открытие» запускает двигатель, открывая дверь, входное действие в состоянии «закрытие» запускает двигатель в другом направлении, закрывающем дверь. Государства «открылись» и «закрыто» останавливают двигатель, когда он полностью открыт или закрыт. Они сигнализируют внешнему миру (например, на другие государственные машины) ситуацию: «дверь открыта» или «дверь закрыта».

Мученика: FSM также использует входные действия, т.е. вывод зависит от ввода и состояния. Использование Meely FSM часто приводит к уменьшению количества состояний. На примере на рисунке 7 показан Mealy FSM, реализующий то же поведение, что и в примере MOORE (поведение зависит от реализованной модели выполнения FSM и будет работать, например, для виртуального FSM , но не для FSM, управляемой событиями ). Существует два входных действий (i :): «Запустите двигатель, чтобы закрыть дверь, если прибудет command_close» и «Пуск в другом направлении, чтобы открыть дверь, если прибудет Command_open». Промежуточные состояния «открытие» и «закрытие» не показаны.

Секвенсоры

Секвенсоры (также называемые генераторами ) представляют собой подкласс акцепторов и преобразователей, которые имеют однобуквенное входное алфавит. Они создают только одну последовательность, которая может рассматриваться как выходная последовательность выходов акцептора или преобразователя. ^{[ 6 ]}

Детерминизм

Дальнейшее различие между детерминированными ( DFA ) и нетерминированными ( NFA , GNFA ) автоматами. В детерминированном автомате каждое состояние имеет ровно один переход для каждого возможного ввода. В нетерминированном автомате вход может привести к одному, более одного или отсутствию перехода для данного состояния. Алгоритм конструкции Powerset может превратить любой неэнергинизм автомата в (обычно более сложный) детерминированный автомат с идентичной функциональностью.

Машина с конечным состоянием с одним состоянием называется «комбинаторной FSM». Это позволяет только действия при переходе в состояние. Эта концепция полезна в тех случаях, когда для совместной работы требуется ряд конечных штатных машин, и когда удобно рассматривать чисто комбинаторную часть как форму FSM в соответствии с инструментами проектирования. ^{[ 11 ]}

Альтернативная семантика

Существуют другие наборы семантики, доступных для представления государственных машин. Например, есть инструменты для моделирования и разработки логики для встроенных контроллеров. ^{[ 12 ]} Они объединяют иерархические государственные машины (которые обычно имеют более чем одно современное состояние), потоковые графики и таблицы истины в один язык, что приводит к другому формализму и набору семантики. ^{[ 13 ]} Эти графики, как и Хареля , оригинальные государственные машины ^{[ 14 ]} Поддерживать иерархически вложенные государства, ортогональные регионы , действия государства и переходные действия. ^{[ 15 ]}

Математическая модель

В соответствии с общей классификацией обнаружены следующие формальные определения.

Детерминированная машина с конечным состоянием или детерминированный акцептор конечного состояния -это квинтэкл $(\Sigma ,S,s_{0},\delta ,F)$ , где:

$\Sigma$ является входным алфавитом (конечный непустые набор символов);
$S$ является конечным непустым набором состояний;
$s_{0}$ это начальное состояние, элемент $S$ ;
$\delta$ Функция трансляции штата: $\delta :S\times \Sigma \rightarrow S$ (в нетерминированном конечном автомате это было бы $\delta :S\times \Sigma \rightarrow {\mathcal {P}}(S)$ IE $\delta$ вернет набор состояний);
$F$ является набором конечных состояний, (возможно, пустого) подмножества $S$ .

Как для детерминированных, так и для не определенных FSMS, это традиционно разрешать $\delta$ быть частичной функцией , т.е. $\delta (s,x)$ не должно быть определено для каждой комбинации $s\in S$ и $x\in \Sigma$ Полем Если FSM $M$ в состоянии $s$ , Следующий символ $x$ и $\delta (s,x)$ не определено, тогда $M$ может объявить об ошибке (то есть отклонить вход). Это полезно в определениях общих государственных машин, но менее полезно при преобразовании машины. Некоторые алгоритмы в их форме по умолчанию могут потребовать общих функций.

Конечный штат машина обладает той же вычислительной мощностью, что и машина Тьюринга , которая ограничена таким образом, что его голова может выполнять только операции «чтение», и всегда должна двигаться слева направо. То есть каждый формальный язык, принятый конечным штатом, принимается таким видом ограниченного машины Тьюринга, и наоборот. ^{[ 16 ]}

Датчик конечного состояния -это Sextuple $(\Sigma ,\Gamma ,S,s_{0},\delta ,\omega )$ , где:

$\Sigma$ является входным алфавитом (конечный непустые набор символов);
$\Gamma$ является выходным алфавитом (конечный непустые набор символов);
$S$ является конечным непустым набором состояний;
$s_{0}$ это начальное состояние, элемент $S$ ;
$\delta$ Функция трансляции штата: $\delta :S\times \Sigma \rightarrow S$ ;
$\omega$ это выходная функция.

Если выходная функция зависит от состояния и входного символа ( $\omega :S\times \Sigma \rightarrow \Gamma$ ) это определение соответствует модели Mealy и может быть смоделировано как мученика . Если выходная функция зависит только от состояния ( $\omega :S\rightarrow \Gamma$ ) это определение соответствует модели Мура и может быть смоделировано как машина Мура . Конечно-состояние машина без выходной функции вообще известна как полуавтоматон или переходная система .

Если мы игнорируем первый выходной символ машины Мура, $\omega (s_{0})$ , затем его можно легко преобразовать в выходную, эквивалентную машину, установив выходную функцию каждого мученого перехода (т.е. маркировка каждого края) с помощью выходного символа, данного состояния Мур назначения. Преобразование конверса менее проста, потому что состояние машины может иметь разные выходные метки на своих входящих переходах (ребра). Каждое такое состояние необходимо разделить в нескольких состояниях машины Мура, одно для каждого символа вывода инцидента. ^{[ 17 ]}

Оптимизация

Оптимизация FSM означает поиск машины с минимальным количеством состояний, которые выполняют ту же функцию. Самый быстро известный алгоритм, делающий это, - это алгоритм минимизации Hopcroft . ^{[ 18 ]}^{[ 19 ]} Другие методы включают в себя использование таблицы последствий или процедуру сокращения Мура. ^{[ 20 ]} Кроме того, ациклические FSA могут быть минимизированы в линейное время . ^{[ 21 ]}

Выполнение

Аппаратные приложения

В цифровой схеме FSM может быть построен с использованием программируемого логического устройства , программируемого логического контроллера , логических ворот и шлепанцев или реле . Более конкретно, аппаратная реализация требует регистра для хранения переменных состояния, блока комбинационной логики , который определяет переход состояния, и второй блок комбинационной логики, который определяет выход FSM. Одной из классических аппаратных реализаций является контроллер Richards .

У машины Медведева выход непосредственно подключен к шлепанцам состояния, минимизируя временную задержку между шлепанцами и выходными. ^{[ 22 ]}^{[ 23 ]}

Через кодирование состояний для низкомопроводителей может быть оптимизировано машины для минимизации энергопотребления.

Программные приложения

Следующие концепции обычно используются для создания программных приложений с помощью конечных состояний:

Конечные машины и компиляторы

Конечные автоматы часто используются на фронте компиляторов языка программирования. Такой фронт может содержать несколько конечных штатных машин, которые реализуют лексический анализатор и анализатор. Начиная с последовательности символов, лексический анализатор создает последовательность языковых токенов (таких как зарезервированные слова, литералы и идентификаторы), из которой анализатор строит дерево синтаксиса. Лексический анализатор и анализатор обрабатывают регулярные и беззаботные части грамматики языка программирования. ^{[ 24 ]}

Смотрите также

Ссылки

^ Ван, Jiacun (2019). Формальные методы в информатике . CRC Press. п. 34. ISBN 978-1-4987-7532-8 .
^ «Конечные государственные машины - блестящая математика и наука вики» . Brilliant.org . Получено 2018-04-14 .
^ Белцер, Джек; Хольцман, Альберт Джордж; Кент, Аллен (1975). Энциклопедия компьютерных наук и техники . Тол. 25. США: CRC Press. п. 73. ISBN 978-0-8247-2275-3 .
^ Jump up to: ^а ^{беременный} Коши, Томас (2004). Дискретная математика с приложениями . Академическая пресса. п. 762. ISBN 978-0-12-421180-3 .
^ Райт, Дэвид Р. (2005). «Конечные государственные машины» (PDF) . CSC215 Примечания к классу . Дэвид Р. Райт Веб -сайт, Н. Каролина штат Univ. Архивировано из оригинала (PDF) 2014-03-27 . Получено 2012-07-14 .
^ Jump up to: ^а ^{беременный} Келлер, Роберт М. (2001). «Классификаторы, акцепторы, преобразователи и секвенсоры» (PDF) . Информатика: абстракция к реализации (PDF) . Харви Мадд Колледж. п. 480.
^ Джон Э. Хопкрофт и Джеффри Д. Уллман (1979). Введение в теорию автоматов, языки и вычисления . Чтение/Ма: Аддисон-Уэсли. ISBN 978-0-201-02988-8 .
^ Пули, Марк; Кохлас, Юрг (2011). Общий вывод: объединяющая теория для автоматических рассуждений . Джон Уайли и сыновья. Глава 6. Оценка алгебры для задач пути, с. 223 в частности. ISBN 978-1-118-01086-0 .
^ Jacek Jonczy (Jun 2008). «Проблемы алгебраического пути» (PDF) . Архивировано из оригинала (PDF) 2014-08-21 . Получено 2014-08-20 . , с. 34
^ Фелкин М. (2007). Гилле, Фабрис; Гамильтон, Говард Дж. (Ред.). Меры качества в добыче данных - исследования в области вычислительной интеллекта . Тол. 43. Спрингер, Берлин, Гейдельберг. С. 277–278. doi : 10.1007/978-3-540-44918-8_12 . ISBN 978-3-540-44911-9 .
^ Brutscheck, M., Berger, S., Franke, M., Schwarzbacher, A., Becker, S.: Процедура структурного деления для эффективного анализа IC. IET Ирландии Конференция сигналов и систем, (ISSC 2008), с.18–23. Голуэй, Ирландия, 18–19 июня 2008 г. [1]
^ «Tiwari, A. (2002). Формальная семантика и методы анализа для моделей Simulink Stateflow» (PDF) . SRI.com . Получено 2018-04-14 .
^ Hamon, G. (2005). Денотационная семантика для Stateflow . Международная конференция по встроенному программному обеспечению. Джерси -Сити, Нью -Джерси: ACM. С. 164–172. Citeseerx 10.1.1.89.8817 .
^ «Harel, D. (1987). Визуальный формализм для сложных систем. Наука компьютерного программирования, 231–274» (PDF) . Архивировано из оригинала (PDF) 2011-07-15 . Получено 2011-06-07 .
^ "Alur, R., Kanade, A., Ramesh, S. & Shashidhar, KC (2008). Символический анализ для улучшения моделирования моделей Simulink/Stateflow. Международная конференция по встроенному программному обеспечению (стр. 89–98). , GA: ACM » (PDF) . Архивировано из оригинала (PDF) 2011-07-15.
^ Черный, Пол Е (12 мая 2008 г.). «Конечный штат Машина» . Словарь алгоритмов и структур данных . США Национальный институт стандартов и технологий . Архивировано из оригинала 13 октября 2018 года . Получено 2 ноября 2016 года .
^ Андерсон, Джеймс Эндрю; Head, Thomas J. (2006). Теория автоматов с современными приложениями . Издательство Кембриджского университета. С. 105–108. ISBN 978-0-521-84887-9 .
^ Хопкрофт, Джон Э. (1971). N n log n -алгоритм для минимизации состояний в конечном автомате (PDF) (технический отчет). Тол. CS-TR-71-190. Стэнфорд Унив. ^{[ Постоянная мертвая ссылка ]}
^ Алмейда, Марко; Морейра, Нельма; Рейс, Рожерио (2007). О производительности алгоритмов минимизации автоматов (PDF) (технический отчет). Тол. DCC-2007-03. Porto Univ. Архивировано из оригинала (PDF) 17 января 2009 года . Получено 25 июня 2008 года .
^ Эдвард Ф. Мур (1956). CE Shannon и J. McCarthy (Ed.). «Геданкен-эксперименты на последовательных машинах». Анналы математических исследований . 34 Издательство Принстонского университета: 129–153. Здесь: Теорема 4, с.142.
^ Revuz, D. (1992). «Минимизация ациклических автоматов в линейное время». Теоретическая информатика . 92 : 181–189. doi : 10.1016/0304-3975 (92) 90142-3 .
^ Kaeslin, Hubert (2008). «Мили, Мур, Медведевский тип и комбинаторные выходные биты» . Цифровая интегрированная конструкция схемы: от архитектур VLSI до изготовления CMOS . Издательство Кембриджского университета. п. 787. ISBN 978-0-521-88267-5 .
^ Слайды архивировали 18 января 2017 года на машине Wayback , синхронные конечные государственные машины; Дизайн и поведение , Университет прикладных наук Гамбург , с.18
^ Ахо, Альфред В . ; Сети, Рави ; Уллман, Джеффри Д. (1986). Компиляторы: принципы, методы и инструменты (1 -е изд.). Аддисон-Уэсли . ISBN 978-0-201-10088-4 .

Дальнейшее чтение

Общий

Сакаровач, Жак (2009). Элементы теории автоматов . Перевод с французов Рувимом Томасом. Издательство Кембриджского университета . ISBN 978-0-521-84425-3 Полем ZBL 1188.68177 .
Вагнер Ф., «Программное обеспечение для моделирования с конечными государственными машинами: практическое подход», Auerbach Publications, 2006, ISBN 0-8499-8086-3 .
ITU-T, рекомендация Z.100 Спецификация и язык описания (SDL)
Самк М., Практические государственные марки в C/C ++ , CMP Books, 2002, ISBN 1-57820-110-1 .
Somek, M., Практический UML StateCharts в C/C ++, 2 -е издание , Newnes, 2008, ISBN 0-7506-8706-1 .
Gardner, T., Advanced State Management Archived 2008-11-19 на The Wayback Machine , 2007
Cassandras, C., Lafortune, S., «Введение в дискретные системы событий». Kluwer, 1999, ISBN 0-7923-8609-4 .
Тимоти Кам, Синтез конечных состояний машин: функциональная оптимизация . Kluwer Academic Publishers, Boston 1997, ISBN 0-7923-9842-4
Тизиано Вилла, Синтез конечных государственных машин: логическая оптимизация . Kluwer Academic Publishers, Boston 1997, ISBN 0-7923-9892-0
Кэрролл Дж., Лонг Д. Теория конечных автоматов с введением в формальные языки . Prentice Hall, Englewood Cliffs, 1989.
Кохави З., Переключение и конечная теория автоматов . МакГроу-Хилл, 1978.
Джилл А., Введение в теорию конечных штатных машин . McGraw-Hill, 1962.
Гинзбург С., Введение в теорию математических машин . Аддисон-Уэсли, 1962.

Машины с конечным состоянием (теория автоматов) в теоретической информатике

Арбиб, Майкл А. (1969). Теории абстрактных автоматов (1 -е изд.). Englewood Cliffs, NJ: Prentice-Hall, Inc. ISBN 978-0-13-913368-8 .
Боброу, Леонард С.; Арбиб, Майкл А. (1974). Дискретная математика: прикладная алгебра для компьютерной и информационной науки (1 -е изд.). Филадельфия: WB Saunders Company, Inc. ISBN 978-0-7216-1768-8 .
Бут, Тейлор Л. (1967). Последовательные машины и теория автоматов (1 -е изд.). Нью-Йорк: John Wiley and Sons, Inc. Библиотека Каталога карт Конгресса № 67-25924.
Булос, Джордж; Джеффри, Ричард (1999) [1989]. Вычислительность и логика (3 -е изд.). Кембридж, Англия: издательство Кембриджского университета. ISBN 978-0-521-20402-6 .
Брукшир, Дж. Гленн (1989). Теория вычислений: формальные языки, автоматы и сложность . Redwood City, Калифорния: Benjamin/Cummings Publish Company, Inc. ISBN 978-0-8053-0143-4 .
Дэвис, Мартин; Сигал, Рон; Weyuker, Elaine J. (1994). Вычислительность, сложность, языки и логика: основы теоретической информатики (2 -е изд.). Сан -Диего: Академическая пресса, Харкорт, Брэйс и Компания. ISBN 978-0-12-206382-4 .
Хопкрофт, Джон; Уллман, Джеффри (1979). Введение в теорию автоматов, языки и вычисления (1 -е изд.). Чтение Мессы: Аддисон-Уэсли. ISBN 978-0-201-02988-8 .
Hopcroft, John E.; Мотвани, Раджив; Уллман, Джеффри Д. (2001). Введение в теорию автоматов, языки и вычисления (2 -е изд.). Чтение Мессы: Аддисон-Уэсли. ISBN 978-0-201-44124-6 .
Хопкин, Дэвид; Мосс, Барбара (1976). Автоматический . Нью-Йорк: Elsevier North-Holland. ISBN 978-0-444-00249-5 .
Выбор, Декстер С. (1997). Автоматы и вычислительность (1 -е изд.). Нью-Йорк: Springer-Verlag. ISBN 978-0-387-94907-9 .
Льюис, Гарри Р .; Пападимитриу, Кристос Х. (1998). Элементы теории вычислений (2 -е изд.). Верхняя Седл-Ривер, Нью-Джерси: Прентис-Холл. ISBN 978-0-13-262478-7 .
Линц, Питер (2006). Формальные языки и автоматы (4 -е изд.). Садбери, Массачусетс: Джонс и Бартлетт. ISBN 978-0-7637-3798-6 .
Мински, Марвин (1967). Вычисление: конечные и бесконечные машины (1 -е изд.). Нью-Джерси: Прентис-Холл.
Papadimitriou, Christos (1993). Вычислительная сложность (1 -е изд.). Аддисон Уэсли. ISBN 978-0-201-53082-7 .
Пиппенгер, Николас (1997). Теории вычисления (1 -е изд.). Кембридж, Англия: издательство Кембриджского университета. ISBN 978-0-521-55380-3 .
Роджер, Сьюзен; Финли, Томас (2006). JFLAP: интерактивные формальные языки и пакет автоматов (1 -е изд.). Садбери, Массачусетс: Джонс и Бартлетт. ISBN 978-0-7637-3834-1 .
SIPSER, Michael (2006). Введение в теорию вычислений (2 -е изд.). Бостонская масса: технология курса Томсона. ISBN 978-0-534-95097-2 .
Вуд, Дерик (1987). Теория вычислений (1 -е изд.). Нью -Йорк: Harper & Row, Publishers, Inc. ISBN 978-0-06-047208-5 .

Абстрактные государственные машины в теоретической информатике

Гуревич, Юрий (июль 2000 г.). «Последовательные абстрактные машины штата захватывают последовательные алгоритмы» (PDF) . ACM транзакции на вычислительной логике . 1 (1): 77–111. Citeseerx 10.1.1.146.3017 . doi : 10.1145/343369.343384 . S2CID 2031696 .

Машинное обучение с использованием алгоритмов конечных состояний

Митчелл, Том М. (1997). Машинное обучение (1 -е изд.). Нью-Йорк: WCB/McGraw-Hill Corporation. ISBN 978-0-07-042807-2 .

Аппаратное проектирование: минимизация состояний и синтез последовательных схем

Бут, Тейлор Л. (1967). Последовательные машины и теория автоматов (1 -е изд.). Нью-Йорк: John Wiley and Sons, Inc. Библиотека Каталога карт Конгресса № 67-25924.
Бут, Тейлор Л. (1971). Цифровые сети и компьютерные системы (1 -е изд.). Нью -Йорк: John Wiley and Sons, Inc. ISBN 978-0-471-08840-0 .
McCluskey, EJ (1965). Введение в теорию переключения цепей (1 -е изд.). Нью-Йорк: McGraw-Hill Book Company, Inc. Библиотека Каталога карт Конгресса № 65-17394.
Хилл, Фредрик Дж.; Петерсон, Джеральд Р. (1965). Введение в теорию переключения цепей (1 -е изд.). Нью-Йорк: McGraw-Hill Book Company. Каталог библиотеки Конгресса № 65-17394.

Конечные процессы цепи марковки

"Мы можем думать о цепи Маркова как о процессе, который последовательно перемещается через набор состояний 1 _{утверждать} , s ₂ ,…, s _r . ... если он находится в состоянии , _это переходит к следующей остановке, чтобы S _J с Вероятность p _ij .

Конечные процессы марковской цепь также известны как подборы конечного типа .

Бут, Тейлор Л. (1967). Последовательные машины и теория автоматов (1 -е изд.). Нью-Йорк: John Wiley and Sons, Inc. Библиотека Каталога карт Конгресса № 67-25924.
Кемени, Джон Г.; Миркил, Хазлтон; Снелл, Дж. Лори; Томпсон, Джеральд Л. (1959). Конечные математические структуры (1 -е изд.). Englewood Cliffs, NJ: Prentice-Hall, Inc. Каталог карт Конгресса № 59-12841. Глава 6 «Конечные марковские цепи».

Внешние ссылки

Конечный государственный автомат в Curlie
Моделирование простого поведения ИИ с использованием примера использования конечного состояния в видеоиграх
Бесплатный онлайн-словарь вычислений описание конечных состояний машин
NIST Dictionary of Algorithms и Structures Описание конечных машин
Краткий обзор типов государственных машин , сравнивая теоретические аспекты Mealy, Moore, Harel & Uml State Machines.

[1] Ван, Jiacun (2019). Формальные методы в информатике . CRC Press. п. 34. ISBN 978-1-4987-7532-8 .

[2] «Конечные государственные машины - блестящая математика и наука вики» . Brilliant.org . Получено 2018-04-14 .

[Belzer-3] Белцер, Джек; Хольцман, Альберт Джордж; Кент, Аллен (1975). Энциклопедия компьютерных наук и техники . Тол. 25. США: CRC Press. п. 73. ISBN 978-0-8247-2275-3 .

[Koshy-4] Jump up to: ^а ^{беременный} Коши, Томас (2004). Дискретная математика с приложениями . Академическая пресса. п. 762. ISBN 978-0-12-421180-3 .

[⁇⁇⁇?-5] Райт, Дэвид Р. (2005). «Конечные государственные машины» (PDF) . CSC215 Примечания к классу . Дэвид Р. Райт Веб -сайт, Н. Каролина штат Univ. Архивировано из оригинала (PDF) 2014-03-27 . Получено 2012-07-14 .

[Keller2001-6] Jump up to: ^а ^{беременный} Келлер, Роберт М. (2001). «Классификаторы, акцепторы, преобразователи и секвенсоры» (PDF) . Информатика: абстракция к реализации (PDF) . Харви Мадд Колледж. п. 480.

[7] Джон Э. Хопкрофт и Джеффри Д. Уллман (1979). Введение в теорию автоматов, языки и вычисления . Чтение/Ма: Аддисон-Уэсли. ISBN 978-0-201-02988-8 .

[PoulyKohlas2012-8] Пули, Марк; Кохлас, Юрг (2011). Общий вывод: объединяющая теория для автоматических рассуждений . Джон Уайли и сыновья. Глава 6. Оценка алгебры для задач пути, с. 223 в частности. ISBN 978-1-118-01086-0 .

[9] Jacek Jonczy (Jun 2008). «Проблемы алгебраического пути» (PDF) . Архивировано из оригинала (PDF) 2014-08-21 . Получено 2014-08-20 . , с. 34

[10] Фелкин М. (2007). Гилле, Фабрис; Гамильтон, Говард Дж. (Ред.). Меры качества в добыче данных - исследования в области вычислительной интеллекта . Тол. 43. Спрингер, Берлин, Гейдельберг. С. 277–278. doi : 10.1007/978-3-540-44918-8_12 . ISBN 978-3-540-44911-9 .

[11] Brutscheck, M., Berger, S., Franke, M., Schwarzbacher, A., Becker, S.: Процедура структурного деления для эффективного анализа IC. IET Ирландии Конференция сигналов и систем, (ISSC 2008), с.18–23. Голуэй, Ирландия, 18–19 июня 2008 г. [1]

[12] «Tiwari, A. (2002). Формальная семантика и методы анализа для моделей Simulink Stateflow» (PDF) . SRI.com . Получено 2018-04-14 .

[13] Hamon, G. (2005). Денотационная семантика для Stateflow . Международная конференция по встроенному программному обеспечению. Джерси -Сити, Нью -Джерси: ACM. С. 164–172. Citeseerx 10.1.1.89.8817 .

[14] «Harel, D. (1987). Визуальный формализм для сложных систем. Наука компьютерного программирования, 231–274» (PDF) . Архивировано из оригинала (PDF) 2011-07-15 . Получено 2011-06-07 .

[15] "Alur, R., Kanade, A., Ramesh, S. & Shashidhar, KC (2008). Символический анализ для улучшения моделирования моделей Simulink/Stateflow. Международная конференция по встроенному программному обеспечению (стр. 89–98). , GA: ACM » (PDF) . Архивировано из оригинала (PDF) 2011-07-15.

[16] Черный, Пол Е (12 мая 2008 г.). «Конечный штат Машина» . Словарь алгоритмов и структур данных . США Национальный институт стандартов и технологий . Архивировано из оригинала 13 октября 2018 года . Получено 2 ноября 2016 года .

[AndersonHead2006-17] Андерсон, Джеймс Эндрю; Head, Thomas J. (2006). Теория автоматов с современными приложениями . Издательство Кембриджского университета. С. 105–108. ISBN 978-0-521-84887-9 .

[18] Хопкрофт, Джон Э. (1971). N n log n -алгоритм для минимизации состояний в конечном автомате (PDF) (технический отчет). Тол. CS-TR-71-190. Стэнфорд Унив. ^{[ Постоянная мертвая ссылка ]}

[19] Алмейда, Марко; Морейра, Нельма; Рейс, Рожерио (2007). О производительности алгоритмов минимизации автоматов (PDF) (технический отчет). Тол. DCC-2007-03. Porto Univ. Архивировано из оригинала (PDF) 17 января 2009 года . Получено 25 июня 2008 года .

[20] Эдвард Ф. Мур (1956). CE Shannon и J. McCarthy (Ed.). «Геданкен-эксперименты на последовательных машинах». Анналы математических исследований . 34 Издательство Принстонского университета: 129–153. Здесь: Теорема 4, с.142.

[21] Revuz, D. (1992). «Минимизация ациклических автоматов в линейное время». Теоретическая информатика . 92 : 181–189. doi : 10.1016/0304-3975 (92) 90142-3 .

[22] Kaeslin, Hubert (2008). «Мили, Мур, Медведевский тип и комбинаторные выходные биты» . Цифровая интегрированная конструкция схемы: от архитектур VLSI до изготовления CMOS . Издательство Кембриджского университета. п. 787. ISBN 978-0-521-88267-5 .

[23] Слайды архивировали 18 января 2017 года на машине Wayback , синхронные конечные государственные машины; Дизайн и поведение , Университет прикладных наук Гамбург , с.18

[24] Ахо, Альфред В . ; Сети, Рави ; Уллман, Джеффри Д. (1986). Компиляторы: принципы, методы и инструменты (1 -е изд.). Аддисон-Уэсли . ISBN 978-0-201-10088-4 .

[ 1 ]

[ 2 ]

[ 3 ]

[ 4 ]

[ 5 ]

[ 6 ]

[ 7 ]

[ 8 ]

[ 9 ]

[ 10 ]

[ 11 ]

[ 12 ]

[ 13 ]

[ 14 ]

[ 15 ]

[ 16 ]

[ 17 ]

[ 18 ]

[ 19 ]

[ 20 ]

[ 21 ]

[ 22 ]

[ 23 ]

[ 24 ]

v Т и Цифровая электроника
Components	Transistor Resistor Inductor Capacitor Printed electronics Printed circuit board Electronic circuit Flip-flop Memory cell Combinational logic Sequential logic Logic gate Boolean circuit Integrated circuit (IC) Hybrid integrated circuit (HIC) Mixed-signal integrated circuit Three-dimensional integrated circuit (3D IC) Emitter-coupled logic (ECL) Erasable programmable logic device (EPLD) Macrocell array Programmable logic array (PLA) Programmable logic device (PLD) Programmable Array Logic (PAL) Generic Array Logic (GAL) Complex programmable logic device (CPLD) Field-programmable gate array (FPGA) Field-programmable object array (FPOA) Application-specific integrated circuit (ASIC) Tensor Processing Unit (TPU)
Theory	Digital signal Boolean algebra Logic synthesis Logic in computer science Computer architecture Digital signal Digital signal processing Circuit minimization Switching circuit theory Gate equivalent
Design	Logic synthesis Place and route Placement Routing Transaction-level modeling Register-transfer level Hardware description language High-level synthesis Formal equivalence checking Synchronous logic Asynchronous logic Finite-state machine Hierarchical state machine
Applications	Computer hardware Hardware acceleration Digital audio radio Digital photography Digital telephone Digital video cinematography television Electronic literature
Design issues	Metastability Runt pulse