Halbach Array

Диаграмма потока массива Halbach

Массив Halbach, показывающий ориентацию магнитного поля каждого произведения. Этот массив даст сильное поле внизу, в то время как поле выше отменится.

Массив Halbach ( Немецкий: [ˈhalbax] ) - это особое расположение постоянных магнитов , которое дополняет магнитное поле на одной стороне массива при отмене поля до нуля с другой стороны. Это достигается путем наличия пространственно вращающегося рисунка намагниченности.

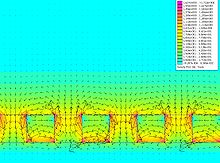
Вращающийся рисунок постоянных магнитов (на передней поверхности; слева, вверх, вправо, вниз) может быть продолжен на неопределенный срок и оказывает тот же эффект. Эффект этого расположения примерно аналогично многим подковообразным магнитам, расположенным рядом друг с другом, прикасающимися к аналогичным полюсам.

Этот магнитный процесс ориентации повторяет, что применяется с помощью магнитной записи ленты к магнитному покрытию ленты во время процесса записи. Принцип был дополнительно описан Джеймсом (Джимом) М. Вином из Магнепана в 1970 году, для идеального случая непрерывной вращающейся намагниченности, вызванной односторонней полосовой катушкой.

Эффект был также обнаружен Джоном К. Маллинсоном в 1973 году, и эти «односторонние поток» были первоначально описаны им как «любопытство», хотя в то время он узнал по этому открытию потенциал значительных улучшений в магнитной ленте технология.

Физик Клаус Халбах , в то время как в Национальной лаборатории Лоуренса Беркли в 1980 -х годах независимо изобрел массив Halbach для фокусировки лучей ускорителя частиц.

Линейные массивы

Ориентация сильных и слабых сторон в линейной массиве Halbach

Намагничение

Отмена магнитных компонентов, приводящих к одностороннему потоку

Хотя это распределение магнитного потока кажется несколько непреодолимым для тех, кто знаком с простыми магнитами или соленоидами , причина этого распределения потока может быть интуитивно визуализирована с использованием исходной диаграммы Маллинсона (обратите внимание, что он использует отрицательный компонент Y , в отличие от диаграммы в статье Маллинсона. ) Диаграмма показывает поле из полосы ферромагнитного материала с чередующейся намагничностью в направлении Y (вверху слева) и в направлении x (вверху справа). Обратите внимание, что поле над плоскостью находится в одном направлении для обеих структур, но поле под плоскостью находится в противоположных направлениях. Эффект наложения обеих этих структур показан на рисунке.

Важнейшим моментом является то, что поток отменится ниже плоскости и усиливается над плоскостью . Фактически, любая схема намагничивания, где компоненты намагниченности $\pi /2$ вне фазы друг с другом приведут к одностороннему потоку. Математическое преобразование, которое сдвигает фазу всех компонентов некоторых функций $\pi /2$ называется трансформацией Гильберта ; Следовательно, компоненты вектора намагничивания могут быть любой парой гильберт-трансформирования (самой простой из которых просто является просто $\sin(x)\cos(y)$, как показано на диаграмме выше).

Магнитное поле вокруг бесконечной массивы хальбах кубических магнитов. Поле не отменяется идеально из -за используемых дискретных магнитов.

Поле на некалирующей стороне идеального, непрерывно различающегося, бесконечная массива имеет форму

$F(x,y)=F_{0}e^{ikx}e^{-ky},$

где

$F(x,y)$ Поле в форме $F_{x}+iF_{y}$,

$F_{0}$ величина поля на поверхности массива,

$k$ это волновое число (то есть пространственная частота) $2\pi /\lambda .$

Приложения

Преимущества односторонних распределений потока двойные:

• Поле в два раза больше на стороне, на которой поток ограничен (в идеализированном случае).
• На противоположной стороне) не произведено бездомное поле (в идеальном случае). Это помогает с полевым ограничением, как правило, проблема в конструкции магнитных структур.

Таким образом, они имеют удивительное количество применений, начиная от плоских холодильников до промышленных применений, таких как бесщеточный двигатель постоянного тока , голосовые катушки , Магнитное нацеливание на лекарства к высокотехнологичным приложениям, таким как магниты Wiggler, используемые в акселераторах частиц и свободные электронные лазеры .

Поезд ​ ​ и индуцированная ракетная система Используйте массив Halbach, чтобы поднять поезд, отталкивая петли проволоки на дорожке.

Магнитная просмотра пленка, показывающая намагниченность магнита с плоским холодильником

Гибкие гибкие (не жесткие керамические ферритовые ) магниты создаются с шаблоном намагничивания Halbach для более сильной силы удержания при прикреплении к плоской ферромагнитной поверхности (например, дверь холодильника), чем сила удержания от равномерной намагниченности. пластиковом или резине), который подвергается воздействию рисунка поля намагничивания Халбаха при экструдированном Они сделаны из порошкообразного феррита, смешанного в гибком связующем (например , просмотреть с помощью магнитной пленки просмотра ).

Распределение потока для плоского холодильника магнита

Схематическая схема свободного электронного лазера

Масштабирование этой конструкции и добавление верхнего листа дает магнит Wiggler , используемый в синхротронах и свободных электронных лазерах . Магниты Вигглера покачиваются, или колебания, электронный луча, перпендикулярная магнитному полю. По мере того, как электроны подвергаются ускорению, они излучают электромагнитную энергию в своем направлении полета, и, когда они взаимодействуют с уже излученным светом, фотоны вдоль его линии испускаются в фазе, что приводит к «лазерноподобному» монохроматическому и когерентному пучению.

Дизайн, показанный выше, обычно называется Halbach Wiggler. Векторы намагничения в намагниченных простынях вращаются в противоположных чувствах друг к другу; Выше вектор намагничения верхнего листа вращается по часовой стрелке, а вектор намагничения нижнего листа вращает против часовой стрелки. Эта конструкция выбрана так, что x компоненты магнитных полей от отмены листов и компонентов Y усиливались, так что поле дано

$H_{y}\approx \cos(kx),$

где k - волновое число магнитного листа, данное расстоянием между магнитными блоками с тем же вектором намагниченности.

Переменные линейные массивы

Схема массива Halbach, состоящая из серии намагниченных стержней

Равное расположение для переменной массивы Halbach

Серия магнитных стержней, намагниченных, перпендикулярных их осями, может быть расположена в массив Halbach. Если каждый стержень повернут попеременно через 90 °, результирующее поле перемещается от одной стороны плоскости стержней к другой, как показано схематически на рисунке.

Это расположение позволяет полему эффективно включаться и выключать над или ниже плоскости стержней, в зависимости от вращения стержней. Такое устройство делает эффективную механическую магнитную защелку, не требующая мощности. Подробное исследование этого расположения показало, что каждый стержень подвергается сильный крутящий момент от соседних стержней и, следовательно, требует механической стабилизации. Тем не менее, простое и эффективное решение, обеспечивающее как стабилизацию, так и способность повернуть каждый стержень попеременно,-это просто обеспечить равное расположение на каждом стержне, как показано на рисунке.

Цилиндр

Ферромагнитный цилиндр, показывающий различные схемы намагничивания и магнитное поле

Намагничение цилиндра

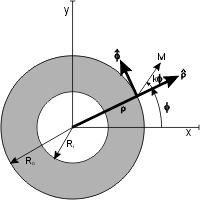
Цилиндр Halbach представляет собой намагниченный цилиндр, состоящий из ферромагнитного материала, производящего (в идеализированном случае) интенсивное магнитное поле, полностью ограниченное в цилиндре, с нулевым полем снаружи. Цилиндры также могут быть намагниченными так, чтобы магнитное поле полностью находилось за пределами цилиндра, с нулевым полем внутри. Несколько распределений намагниченности показаны на рисунках.

Направление намагниченности в ферромагнитном материале, в плоскости перпендикулярно оси цилиндра, дается

$M=M_{r}\left[\cos \left((k-1)\left(\varphi -{\frac {\pi }{2}}\right)\right){\widehat {\rho }}+\sin \left((k-1)\left(\varphi -{\frac {\pi }{2}}\right)\right){\widehat {\varphi }}\right],$

где M _r - ферромагнитная остаточность (A/M). Положительное значение k - 1 дает внутреннее магнитное поле, а отрицательное дает внешнее магнитное поле.

В идеале эти структуры будут созданы из цилиндра бесконечной длины магнитного материала с направлением намагниченности непрерывно изменяющимся. Магнитный поток, созданный этим идеальным дизайном, был бы совершенно равномерным и полностью ограничен либо отверстием цилиндра, либо на внешней стороне цилиндра. Конечно, идеальный случай бесконечной длины не может быть реализован, и на практике конечная длина цилиндров дает конечные эффекты , которые вводят в полевых условиях нерамерность. Сложность изготовления цилиндра с непрерывно изменяющейся намагничностью также обычно приводит к тому, что дизайн разбивается на сегменты.

Приложения

Эти цилиндрические структуры используются в таких устройствах, как бесщеточные двигатели переменного тока, магнитные муфты и цилиндры высокого поля. Как бесщеточные двигатели, так и муфты используют многоцелевые поля:

• Бесщеточные двигатели или генераторы обычно используют цилиндрические конструкции, в которых весь поток ограничен центром отверстия (например, K = 4 выше, 6-полюсный ротор) с катушками AC, также содержащимся в отверстии. Такие конструкции двигателя самостоятельного оборудования или генератора являются более эффективными и производят более высокий крутящий момент или выход, чем обычные конструкции двигателя или генератора.
• Устройства с магнитной связью передают крутящий момент через магнитные прозрачные барьеры (то есть барьер не магнитный или магнитный, но не влияет на приложенное магнитное поле), например, между герметичными контейнерами или судами под давлением. Оптимальные связи крутящего момента состоит из пары коаксиально вложенных цилиндров с противоположными + k и - K , поскольку эта конфигурация является единственной системой бесконечно длинных цилиндров, которая производит крутящий момент. схемами нагрузки В состоянии самой низкой энергии внешний поток внутреннего цилиндра точно соответствует внутреннему потоку внешнего цилиндра. Вращение одного цилиндра относительно другого из этого состояния приводит к восстановительному крутящему моменту.
• Цилиндрические массивы Halbach используются в портативных МРТ -сканерах. Они предлагают потенциал для относительно легкой системы с низким до среднего поля без криогеники , небольшого полоса и без требований к электрической мощности или потребностей рассеивания тепла. Сниженные наружные поля также повышают безопасность и минимизируют помехи окружающим электронным устройствам.

Единообразные поля

Равномерное поле внутри цилиндра Халбаха

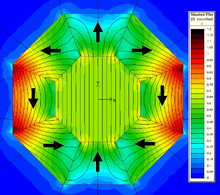
Для особого случая k = 2 поле внутри отверстия однородное и дано

$H=M_{r}\ln \left({\frac {R_{\text{o}}}{R_{\text{i}}}}\right){\widehat {y}},$

где внутренние и внешние радиусы цилиндров находятся R _I и R _O соответственно. H находится в Y. направлении Это самая простая форма цилиндра Halbach, и видно, что если соотношение внешних и внутренних радиусов больше, чем E , поток внутри отверстия фактически превышает остаточность магнитного материала, используемого для создания цилиндра. Тем не менее, необходимо соблюдать осторожность не для производства поле, которое превышает коэрцитивность используемых постоянных магнитов, поскольку это может привести к размагнированию цилиндра и производству гораздо более низкого поля, чем предполагалось.

Три конструкции (a) (b) (c) Создание равномерных магнитных полей в их центральном воздушном зазоре

Эта цилиндрическая конструкция представляет собой только один класс конструкций, которые производят равномерное поле внутри полости в массиве постоянных магнитов. Другие классы дизайна включают в себя дизайн клина, предложенные Abele и Jensen, в которых клинья из намагниченного материала расположены для обеспечения равномерного поля внутри полостей внутри дизайна, как показано.

Направление намагниченности клиньев в (а) можно рассчитать с помощью набора правил, указанных Абеле, и обеспечивает большую свободу в форме полости. Другим классом дизайна является магнитный мангл (б), предложенный Коуи и Кугатом, в котором однородно намагниченные стержни расположены так, что их намагниченность совпадает с набором цилиндра Halbach, как показано для конструкции 6-й рода. Этот дизайн значительно увеличивает доступ к области равномерного поля, за счет объема равномерного поля меньше, чем в цилиндрических конструкциях (хотя эта область может быть увеличена за счет увеличения количества стержней компонентов). Вращение стержней относительно друг друга приводит к многим возможностям, включая динамически переменное поле и различные дипольные конфигурации. Можно видеть, что конструкции, показанные в (а) и (б), тесно связаны с цилиндром k = 2 halbach. Другие очень простые конструкции для равномерного поля включают разделенные магниты с мягким железом возвратом путей, как показано на рисунке (C).

В последние годы эти диполи Halbach были использованы для проведения экспериментов с ЯМР низкого уровня . По сравнению с коммерчески доступной ( Bruker Minispec) стандартной геометрией пластин (C) постоянных магнитов, они, как объяснено выше, предлагают огромный диаметр отверстия, при этом имея достаточно однородное поле.

Вывод в идеальном случае

Метод, используемый для поиска поля, созданного цилиндром, математически очень похож на то, что используется для исследования равномерно намагниченной сферы.

Из-за симметрии расположения вдоль оси цилиндра проблема может рассматриваться как двумерная. Работать в плоскополярных координатах $(r,\theta )$ с ассоциированными единичными векторами ${\hat {\mathbf {r} }}$ и ${\hat {\boldsymbol {\theta }}}$и пусть цилиндр имеет радиальную степень $r_{\mathrm {i} }<r<r_{\mathrm {o} }$Полем Затем намагничивание в стенах цилиндра, которая имеет величину $M_{0}$вращается плавно как

$\mathbf {M} _{\mathrm {cyl} }=M_{0}(\cos \theta \,{\hat {\mathbf {r} }}+\sin \theta \,{\hat {\boldsymbol {\theta }}}),$

Пока намагничность исчезает за стенами, это для отверстия $r<r_{\mathrm {i} }$ и окружение $r>r_{\mathrm {o} }$.

По определению прочность вспомогательного магнитного поля $\mathbf {H}$ связан с магнитизацией и плотностью магнитного потока $\mathbf {B}$ к $\mathbf {B} =\mu _{0}(\mathbf {H} +\mathbf {M} )$Полем Используя закон Гаусса $\nabla \cdot \mathbf {B} =0$, это эквивалентно

$\nabla \cdot \mathbf {H} =-\nabla \cdot \mathbf {M} .$ ( 1 )

Поскольку проблема статична, нет свободных течений, и деривативы на все времена исчезают, поэтому закон Ампера дополнительно требует $\nabla \times \mathbf {H} =0\implies \mathbf {H} =\nabla \varphi$, где $\varphi$ является магнитным скалярным потенциалом (до знака под некоторыми определениями). Заменить это обратно в предыдущее уравнение 1 управляющее $\mathbf {H}$ и $\mathbf {M}$, мы находим, что нам нужно решить

$\nabla ^{2}\varphi =-\nabla \cdot \mathbf {M} ,$ ( 2 )

который имеет форму уравнения Пуассона .

Рассмотрим теперь граничные условия на интерфейсах цилиндров $r=r_{\mathrm {i} }$ и $r=r_{\mathrm {o} }$Полем Интеграция $\nabla \times \mathbf {H} =0$ Через небольшую петлю, преодолевающую границу и применение теоремы Стоукса требует, чтобы параллельный компонент $\mathbf {H}$ непрерывно. Это, в свою очередь, требует, чтобы $\varphi$ непрерывно через границу. (Более правильно это подразумевает, что $\varphi$ Должен отличаться постоянной по физические величины, которые нас интересуют границе, но , поскольку Маленький объем оспаривает границу и примените теорему дивергенции , чтобы найти

$\left[{\frac {\partial \varphi }{\partial r}}\right]=\pm \mathbf {M} \cdot {\hat {\mathbf {r} }},$

где нотация $[f]$ обозначает прыжок в количестве $f$ через границу, и в нашем случае знак негативно при $r=r_{\mathrm {i} }$ и положительный в $r=r_{\mathrm {o} }$Полем Разница знаков обусловлена ​​относительной ориентацией намагниченности и поверхностной, нормальной к части объема интеграции внутри стен цилиндров, противоположной на внутренних и внешних границах.

В плоскополярных координатах дивергенция векторного поля $\mathbf {F} =F_{r}{\hat {\mathbf {r} }}+F_{\theta }{\hat {\boldsymbol {\theta }}}$ дано

$\nabla \cdot \mathbf {F} ={\frac {1}{r}}{\frac {\partial }{\partial r}}(rF_{r})+{\frac {1}{r}}{\frac {\partial F_{\theta }}{\partial \theta }}.$ ( 3 )

Точно так же градиент скалярного поля $f$ дано

$\nabla f={\frac {\partial f}{\partial r}}{\hat {\mathbf {r} }}+{\frac {1}{r}}{\frac {\partial f}{\partial \theta }}{\hat {\boldsymbol {\theta }}}.$ ( 4 )

Объединение этих двух отношений, Лапласиан $\nabla ^{2}f=\nabla \cdot (\nabla f)$ становится

$\nabla ^{2}f={\frac {1}{r}}{\frac {\partial }{\partial r}}\left(r{\frac {\partial f}{\partial r}}\right)+{\frac {1}{r^{2}}}{\frac {\partial ^{2}f}{\partial \theta ^{2}}}.$ ( 5 )

Используя уравнение 3 , дивергенция нагрузки в стенках цилиндра

${\begin{aligned}\nabla \cdot \mathbf {M} _{\mathrm {cyl} }&={\frac {1}{r}}{\frac {\partial }{\partial r}}(rM_{0}\cos \theta )+{\frac {1}{r}}{\frac {\partial }{\partial \theta }}(M_{0}\sin \theta )\\[5pt]&={\frac {M_{0}\cos \theta }{r}}+{\frac {M_{0}\cos \theta }{r}}\\[5pt]&={\frac {2M_{0}\cos \theta }{r}}.\end{aligned}}$

Следовательно, уравнение 2 , которое мы хотим решить, становится с помощью уравнения 5

${\frac {1}{r}}{\frac {\partial }{\partial r}}\left(r{\frac {\partial \varphi }{\partial r}}\right)+{\frac {1}{r^{2}}}{\frac {\partial ^{2}\varphi }{\partial \theta ^{2}}}={\begin{cases}0&r<r_{\mathrm {i} },\\-{\frac {2M_{0}\cos \theta }{r}}&r_{\mathrm {i} }<r<r_{\mathrm {o} },\\0&r>r_{\mathrm {0} }.\end{cases}}$ ( 6 )

Ищите конкретное решение этого уравнения в стенках цилиндра. С учетом задним числом рассмотрим $\varphi _{\mathrm {p} }=r\ln r\cos \theta$, потому что тогда у нас есть

${\begin{aligned}{\frac {1}{r}}{\frac {\partial }{\partial r}}\left(r{\frac {\partial \varphi _{\mathrm {p} }}{\partial r}}\right)&={\frac {1}{r}}{\frac {\partial }{\partial r}}\left[r{\frac {\partial }{\partial r}}(r\ln r\cos \theta )\right]\\[5pt]&={\frac {\cos \theta }{r}}{\frac {\partial }{\partial r}}\left[r(\ln r+1)\right]\\[5pt]&={\frac {\cos \theta }{r}}(\ln r+1+1)\\[5pt]&={\frac {\ln r\cos \theta }{r}}+{\frac {2\cos \theta }{r}}\end{aligned}}$

а также

${\begin{aligned}{\frac {1}{r^{2}}}{\frac {\partial ^{2}\varphi _{\mathrm {p} }}{\partial \theta ^{2}}}&={\frac {1}{r^{2}}}{\frac {\partial ^{2}}{\partial \theta ^{2}}}(r\ln r\cos \theta )\\[5pt]&=-{\frac {\ln r\cos \theta }{r}}.\end{aligned}}$

Следовательно $\nabla ^{2}\varphi _{\mathrm {p} }={\frac {2\cos \theta }{r}}$и сравнение с уравнением 6 показывает, что $-M_{0}\varphi _{\mathrm {p} }=-M_{0}r\ln r\cos \theta$ является подходящим конкретным решением.

Теперь рассмотрим однородное уравнение для уравнения 6 , а именно $\nabla ^{2}\varphi _{\mathrm {h} }=0$Полем Это имеет форму уравнения Лапласа . С помощью метода разделения переменных можно показать, что общее однородное решение, градиент которого периодически в $\theta$ (так, что все физические величины однозначны) определяются

$\varphi _{\mathrm {h} }=A_{0}+B_{0}\theta +C_{0}\ln r+\sum _{n=1}^{\infty }\left(A_{n}r^{n}+B_{n}r^{-n}\right)\cos n\theta +\sum _{n=1}^{\infty }\left(C_{n}r^{n}+D_{n}r^{-n}\right)\sin n\theta ,$

где $A_{i},\ B_{i},\ C_{i},\ D_{i}$ произвольные постоянные. Желаемое решение будет суммой конкретных и однородных решений, которые удовлетворяют граничным условиям. Опять же, с задним числом, давайте немедленно установим большинство констант и утверждаем, что решение

$\varphi ={\begin{cases}\alpha r\cos \theta &r<r_{\mathrm {i} },\\\beta r\cos \theta -M_{0}r\ln r\cos \theta &r_{\mathrm {i} }<r<r_{\mathrm {o} },\\0&r>r_{\mathrm {o} },\end{cases}}$

где сейчас $\alpha ,\ \beta$ являются константами, которые должны быть определены. Если мы можем выбрать константы так, чтобы граничные условия были удовлетворены, то по теореме уникальности для уравнения Пуассона мы должны были найти решение.

Условия непрерывности дают

$\alpha =\beta -M_{0}\ln r_{\mathrm {i} }$ ( 7 )

на внутренней границе и

$\beta -M_{0}\ln r_{\mathrm {o} }=0$ ( 8 )

на внешней границе. Потенциальный градиент имеет непанирующий радиальный компонент $\beta \cos \theta -M_{0}\ln r\cos \theta -M_{0}\cos \theta$ в стенах цилиндра и $\alpha \cos \theta$ в отверстии, и поэтому условия на потенциальной производной становятся

$(\beta \cos \theta -M_{0}\ln r_{\mathrm {i} }\cos \theta -M_{0}\cos \theta )-\alpha \cos \theta =-M_{0}\cos \theta \implies \beta -M_{0}\ln r_{\mathrm {i} }-\alpha =0\implies \alpha =\beta -M_{0}\ln r_{\mathrm {i} }$

на внутренней границе и

$0-(\beta \cos \theta -M_{0}\ln r_{\mathrm {0} }\cos \theta -M_{0}\cos \theta )=M_{0}\cos \theta \implies \beta -M_{0}\ln r_{\mathrm {o} }=0$

на внешней границе. Обратите внимание, что они идентичны уравнениям 7 и 8 , поэтому, действительно, предположение было последовательным. Следовательно, у нас есть $\beta =M_{0}\ln r_{\mathrm {o} }$ и $\alpha =M_{0}\ln \left({\frac {r_{\mathrm {o} }}{r_{\mathrm {i} }}}\right)$, давая решение

$\varphi ={\begin{cases}M_{0}\ln \left({\frac {r_{\mathrm {o} }}{r_{\mathrm {i} }}}\right)r\cos \theta &r<r_{\mathrm {i} },\\M_{0}\ln \left({\frac {r_{\mathrm {o} }}{r}}\right)r\cos \theta &r_{\mathrm {i} }<r<r_{\mathrm {o} },\\0&r>r_{\mathrm {o} }.\end{cases}}$

Следовательно, магнитное поле дается

$\mathbf {H} =\nabla \varphi ={\begin{cases}M_{0}\ln \left({\frac {r_{\mathrm {o} }}{r_{\mathrm {i} }}}\right)\cos \theta \,{\hat {\mathbf {r} }}-M_{0}\ln \left({\frac {r_{\mathrm {o} }}{r_{\mathrm {i} }}}\right)\sin \theta \,{\hat {\boldsymbol {\theta }}}&r<r_{\mathrm {i} },\\M_{0}\cos \theta \left[\ln \left({\frac {r_{\mathrm {o} }}{r}}\right)-1\right]\,{\hat {\mathbf {r} }}-M_{0}\ln \left({\frac {r_{\mathrm {o} }}{r}}\right)\sin \theta \,{\hat {\boldsymbol {\theta }}}&r_{\mathrm {i} }<r<r_{\mathrm {o} },\\0&r>r_{\mathrm {o} },\end{cases}}$

В то время как плотность магнитного потока можно найти повсюду, используя предыдущее определение $\mathbf {B} =\mu _{0}(\mathbf {H} +\mathbf {M} )$Полем В отверстии, где намагничивание исчезает, это уменьшается до $\mathbf {B} _{\mathrm {bore} }={\frac {1}{\mu _{0}}}\mathbf {H} _{\mathrm {bore} }$Полем Следовательно, величина плотности потока есть

$B_{\mathrm {bore} }=\left|\mathbf {B} _{\mathrm {bore} }\right|={\sqrt {\cos ^{2}\theta +\sin ^{2}\theta }}{\frac {M_{0}}{\mu _{0}}}\ln \left({\frac {r_{\mathrm {o} }}{r_{\mathrm {i} }}}\right)={\frac {M_{0}}{\mu _{0}}}\ln \left({\frac {r_{\mathrm {o} }}{r_{\mathrm {i} }}}\right),$

который не зависит от позиции. Точно так же за пределами цилиндра намагничивание также исчезает, и, поскольку магнитное поле исчезает там, плотность потока тоже делает. Таким образом, действительно поле находится внутри и нулевым за пределами идеального цилиндра Халбаха, с величиной в зависимости от его физических измерений.

Изменяя поле

Цилиндры Halbach дают статическое поле. Однако цилиндры могут быть вложены, а путем вращения одного цилиндра относительно другого может быть достигнута отмена поля и регулировка направления. Поскольку внешнее поле цилиндра довольно низкое, относительное вращение не требует сильных сил. В идеальном случае бесконечно длинных цилиндров не потребуется никакой силы для вращения цилиндра по отношению к другому.

Магнитная левитация с использованием плоской массивы Halbach и концентрических обмоток структуры

Сфера

Если двумерные шаблоны магнитного распределения цилиндра Halbach расширены до трех измерений, результатом является сфера Halbach. Эти конструкции имеют чрезвычайно равномерное поле внутри дизайна, так как на них не влияет «конечные эффекты», распространенные в конструкции цилиндра конечной длины. Величина однородного поля для сферы также увеличивается до 4/3 количества для идеальной цилиндрической конструкции с тем же внутренним и внешним радиусом. Однако для сферической структуры доступ к области равномерного поля обычно ограничивается узким отверстием в верхней и нижней части конструкции.

Уравнение для поля в сфере Халбах

$B={\frac {4}{3}}B_{0}\ln \left({\frac {R_{\text{o}}}{R_{\text{i}}}}\right).$

Более высокие поля возможны благодаря оптимизации сферической конструкции, чтобы учитывать тот факт, что он состоит из точечных диполей (а не линейных диполи). Это приводит к растяжению сферы до эллиптической формы и имеет неоднородное распределение намагниченности по компонентным частям. Используя этот метод, а также мягкие части полюса в дизайне, 4,5 т в рабочем томе 20 мм ³ был достигнут Bloch et al. в 1998 году, и это было увеличено до 5 т в 2002 году, Хотя более меньший рабочий объем 0,05 мм ³ Полем Поскольку твердые материалы зависят от температуры, охлаждение всей магнитной массивы может дополнительно увеличить поле в рабочей зоне, как показано Kumada et al. В этой группе также сообщалось о разработке дипольного цилиндра 5,16 T Halbach в 2003 году.

Смотрите также

• Неодимий -магнит
• Постоянный магнит
• Сильная фокусировка
• Inductrack использует массивы Halbach для генерации сильных полей для поездов Maglev
• Катушка Helmholtz может дать очень ровные магнитные поля

Внешние ссылки

• СМИ, связанные с Halbach Array в Wikimedia Commons
• Пассивная левитация вала
• Электрический модельный самолет
• Магнитная система переключения транспортных средств