Модульная решетка

В разделе математики, называемом теорией порядка , модулярная решетка — это решетка , которая удовлетворяет следующему самодвойственному условию :

Модульный закон: $a \leq b$ подразумевает $а \lor (Икс \land б) знак равно (а \lor Икс) \land б$

где $x, a, b$ — произвольные элементы в решетке, ≤ — частичный порядок , а ∨ и ∧ (называемые «соединение» и «встреча» соответственно) — операции решетки. Эта формулировка подчеркивает интерпретацию в терминах проекции на подрешетку $[a, b]$ , факт, известный как теорема об изоморфизме алмаза . ^[1] Альтернативное, но эквивалентное условие, сформулированное в виде уравнения (см. ниже), подчеркивает, что модулярные решетки образуют многообразие в смысле универсальной алгебры .

Модульные решетки естественным образом возникают в алгебре и во многих других областях математики. В этих сценариях модульность является абстракцией 2-й теоремы об изоморфизме . Например, подпространства векторного пространства (и, в более общем смысле, подмодули модуля над кольцом ) образуют модульную решетку.

В не обязательно модулярной решетке все еще могут существовать элементы $b$ , для которых модульный закон выполняется в связи с произвольными элементами $x$ и $a$ (при $a \leq b$ ). Такой элемент называется правомодулярным элементом . В более общем смысле, модульный закон может выполняться для любого $a$ и фиксированной пары $(x, b)$ . Такая пара называется модулярной парой , и существуют различные обобщения модулярности, связанные с этим понятием и с полумодулярностью .

Модульные решетки иногда называют решетками Дедекинда в честь Ричарда Дедекинда , который обнаружил модульную идентичность в нескольких мотивирующих примерах .

Введение

Модульный закон можно рассматривать как ограниченный ассоциативный закон , который соединяет две операции решетки аналогично тому, как ассоциативный закон λ(μ x ) = (λμ) x для векторных пространств связывает умножение в поле и скалярное умножение.

Ограничение $a \leq b$ очевидно необходимо, поскольку оно следует из $a \lor (x \land b) = (a \lor x) \land b$ . Другими словами, ни одна решетка, содержащая более одного элемента, не удовлетворяет неограниченному следствию модулярного закона.

Это легко увидеть ^[2] что $a \lor x$ влечет $a \lor (x \land b) ⩽ (a \lor x) \land b$ в каждой решетке. Следовательно, модульный закон можно также сформулировать как

Модульный закон (вариант): $а \leq б$ подразумевает $(а \lor Икс) \land б \leq а \lor (Икс \land б)$ .

Модульный закон можно выразить в виде уравнения, которое требуется выполнять безоговорочно. Поскольку из $a \leq b$ следует $a = a \land b$ и поскольку $a \land b \leq b$ , замените $a$ на $a \land b$ в определяющем уравнении модульного закона, чтобы получить:

Модульная идентичность: $(а \land б) \lor (Икс \land б) знак равно ((а \land б) \lor Икс) \land б$ .

Это показывает, что, используя терминологию универсальной алгебры , модулярные решетки образуют подмногообразие многообразия решеток . Следовательно, все гомоморфные образы, подрешетки и прямые произведения модулярных решеток снова модулярны.

Примеры

Решетка подмодулей модуля над кольцом модулярна. В частном случае решетка подгрупп абелевой группы модулярна.

Решетка нормальных подгрупп модулярна группы . Но вообще решетка всех подгрупп группы немодулярна. Например, решетка подгрупп группы диэдра восьмого порядка не является модулярной.

Наименьшей немодульной решеткой является «пятиугольная» решетка N _5, состоящая из пяти элементов 0, 1, x , a , b таких, что 0 < x < b < 1, 0 < a < 1 и a не сравнимо с x. или к б . Для этой решетки

Икс ∨ ( а ∧ б ) знак равно Икс ∨ 0 знак равно Икс < б знак равно 1 ∧ б знак равно ( Икс ∨ а ) ∧ б

имеет место, что противоречит модульному закону. Каждая немодулярная решетка содержит копию N ₅ в качестве подрешетки. ^[3]

Характеристики

Любая дистрибутивная решетка модульна. ^[4]^[5]

Дилворт (1954) доказал, что в каждой конечной модулярной решетке количество элементов, не приводимых в объединение, равно количеству элементов, не приводимых в объединение. В более общем смысле, для каждого $k$ количество элементов решетки, которые покрывают ровно $k$ других элементов, равно числу, которые покрываются ровно $k$ другими элементами. ^[6]

Полезное свойство, показывающее, что решетка не является модулярной, заключается в следующем:

Решетка

G

когда для любых

a, b, c \in G

является модулярной тогда и только тогда ,

{\Big (}(c\leq a){\text{ and }}(a\wedge b=c\wedge b){\text{ and }}(a\vee b=c\vee b){\Big )}\Rightarrow (a=c)

Схема доказательства: пусть G модулярна и предпосылка импликации верна. Затем, используя поглощение и модульную идентичность:

c знак равно ( c ∧ б ) ∨ c знак равно ( а ∧ б ) ∨ c равно знак равно а ∧ ( б ∨ c ) знак равно а ∧ ( б ∨ а ) знак а

Для другого направления пусть импликация теоремы выполняется в G. Пусть a , b , c — любые элементы из G, такие что c ⩽ a . Пусть x = ( a ∧ b ) ∨ c , y = a ∧ ( b ∨ c ). Из модульного неравенства сразу следует, что x ≤ y . Если мы покажем, что x ∧ b = y ∧ b , x ∨ b = y ∨ b , то, используя предположение x = y, должно выполняться. Остальная часть доказательства — рутинные манипуляции с инфимами, супремами и неравенствами. ^{[ нужна ссылка ]}

Теорема об изоморфизме алмаза

Для любых двух элементов a , b модулярной решетки можно рассматривать интервалы [ a ∧ b , b ] и [ a , a ∨ b ]. Они соединены сохраняющими порядок картами.

φ: [ а ∧ б , б ] → [ а , а ∨ б ] и

ψ: [ а , а ∨ б ] → [ а ∧ б , б ]

которые определяются формулами φ( x ) = x ∨ a и ψ( y ) = y ∧ b .

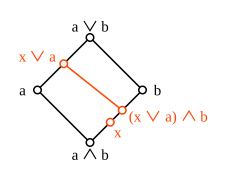
В модулярной решетке отображения φ и ψ, указанные стрелками, являются взаимно обратными изоморфизмами.
Несостоятельность теоремы об изоморфизме алмаза в немодульной решетке.

Композиция ψφ представляет собой сохраняющее порядок отображение интервала [ a ∧ b , b ] в себя, которое также удовлетворяет неравенству ψ(φ( x )) = ( x ∨ a ) ∧ b ≥ x . Пример показывает, что это неравенство, вообще говоря, может быть строгим. Однако в модульной решетке равенство сохраняется. Поскольку двойственное к модулярной решетке снова модулярное, φψ также является единицей на [ a , a ∨ b ], и, следовательно, два отображения φ и ψ являются изоморфизмами между этими двумя интервалами. Этот результат иногда называют теоремой об изоморфизме алмаза для модулярных решеток. Решетка является модулярной тогда и только тогда, когда теорема об изоморфизме алмаза справедлива для каждой пары элементов.

Теорема об изоморфизме алмаза для модульных решеток аналогична второй теореме об изоморфизме в алгебре и является обобщением теоремы о решетке .

Модульные пары и связанные с ними понятия

В любой решетке модулярная пара — это пара ( a, b ) элементов такая, что для всех x, удовлетворяющих a ∧ b ≤ x ≤ b , имеем ( x ∨ a ) ∧ b = x , т. е. если одна половина ромба Для пары справедлива теорема об изоморфизме. ^[7] Элемент b решетки называется правомодулярным элементом, если ( a, b ) является модулярной парой для всех элементов a , а элемент a называется левомодулярным элементом, если ( a, b ) является модулярной парой для всех элементов. б . ^[8]

Решетка, обладающая свойством, что если ( a, b ) — модулярная пара, то ( b, a ) также является модулярной парой, называется M-симметричной решеткой . ^[9] Таким образом, в M-симметричной решетке каждый правомодулярный элемент также является левомодулярным, и наоборот. Поскольку решетка является модулярной тогда и только тогда, когда все пары элементов модулярны, очевидно, что каждая модулярная решетка M-симметрична. В описанной выше решетке N ₅ пара ( b, a ) является модулярной, а пара ( a, b ) — нет. Следовательно, N ₅ не является M-симметричным. Центрированная шестиугольная решетка S ₇ M-симметрична, но не модулярна. Так как N ₅ является подрешеткой в S ₇ , то M-симметричные решетки не образуют подмногообразия многообразия решеток.

М-симметрия не является самодвойственным понятием. Двойственная модулярная пара — это пара, которая является модулярной в дуальной решетке, а решетка называется дуально M-симметричной или M ^*-симметричен , если его двойственный M-симметричен. Можно показать, что конечная решетка модулярна тогда и только тогда, когда она M-симметрична и M ^*-симметричный. Та же эквивалентность справедлива для бесконечных решеток, удовлетворяющих условию возрастающей цепи (или условию нисходящей цепи).

Несколько менее важных понятий также тесно связаны между собой. Решетка является перекрестно-симметричной , если для каждой модулярной пары ( a, b ) пара ( b, a ) дуально модулярна. Кросс-симметрия подразумевает M-симметрию, но не M. ^*-симметрия. Следовательно, кросс-симметрия не эквивалентна двойной кросс-симметрии. Решетка с наименьшим элементом 0 называется ⊥-симметричной, если для каждой модулярной пары ( a, b ), удовлетворяющей условию a ∧ b = 0, пара ( b, a ) также является модулярной.

История

Определение модульности принадлежит Ричарду Дедекинду , который опубликовал большинство соответствующих статей после выхода на пенсию.В статье, опубликованной в 1894 г. ^{[ нужна ссылка ]} он изучал решетки, которые он называл дуальными группами ( нем . Dualgruppen ) как часть своей «алгебры модулей », и заметил, что идеалы удовлетворяют тому, что мы теперь называем модулярным законом. Он также заметил, что для решеток в целом модульный закон эквивалентен двойственному ему закону.

В другой статье 1897 года Дедекинд исследовал решетку дивизоров с НОД и lcm в качестве операций, так что порядок решетки задается делимостью. ^[10]В отступлении он представил и изучил решетки формально в общем контексте. ^[10]^: 10–18 Он заметил, что решетка подмодулей модуля удовлетворяет модулярному тождеству. Такие решетки он назвал двойственными группами модульного типа ( Dualgruppen vom Modultypus ). Он также доказал, что модульное тождество и двойственное ему эквивалентны. ^[10]^: 13

В той же статье Дедекинд также исследовал следующую более сильную форму ^[10]^: 14 модульной идентичности, которая также самодуальна: ^[10]^: 9

( Икс ∧ б ) ∨ ( а ∧ б ) знак равно [ Икс ∨ а ] ∧ б .

Решетки, удовлетворяющие этому тождеству, он назвал дуальными группами идеального типа ( Dualgruppen vom Idealtypus ). ^[10]^: 13 В современной литературе их чаще называют распределительными решетками . Он привел примеры решетки немодулярной и модулярной решетки неидеального типа. ^[10]^: 14

В статье, опубликованной Дедекиндом в 1900 году, решётки были центральной темой: он описал свободную модульную решетку, порожденную тремя элементами, решетку из 28 элементов (см. рисунок). ^[11]

См. также

Модульный граф — класс графов, включающий диаграммы Хассе модульных решеток.
Решетка Янга – Фибоначчи , бесконечная модульная решетка, определенная на строках цифр 1 и 2.
Ортомодулярная решетка
Сверхразрешимая решетка
группа Ивасава

Примечания

^ «Почему модульные решетки важны?» . Математический обмен стеками . Проверено 17 сентября 2018 г.
^ Для любой решетки верно следующее: $а \lor (Икс \land б) \leq (а \lor Икс) \land (а \lor б)$ . Кроме того, всякий раз, когда $a \leq b$ , тогда $a \lor b = b$ .
^ Блит, Т.С. (2005). «Модульные решетки» . Решетки и упорядоченные алгебраические структуры . Университеттекст. Лондон: Спрингер. Теорема 4.4. дои : 10.1007/1-84628-127-X_4 . ISBN 978-1-85233-905-0 .
^ Блит, Т.С. (2005). «Модульные решетки» . Решетки и упорядоченные алгебраические структуры . Университеттекст. Лондон: Спрингер. п. 65. дои : 10.1007/1-84628-127-X_4 . ISBN 978-1-85233-905-0 .
^ В дистрибутивной решетке справедливо следующее: $(a\wedge b)\vee (x\wedge b)=((a\wedge b)\vee x)\wedge ((a\wedge b)\vee b)$ . Кроме того, закон поглощения $(a\wedge b)\vee b=b$ , справедливо для любой решетки. Подстановка этого второго соединения в правую часть первого уравнения дает модульную идентичность.
^ Дилворт, Р.П. (1954), «Доказательство гипотезы о конечных модулярных решетках», Annals of Mathematics , Second Series, 60 (2): 359–364, doi : 10.2307/1969639 , JSTOR 1969639 , MR 0063348 . Перепечатано в Богарт, Кеннет П.; Фриз, Ральф; Кунг, Джозеф PS, ред. (1990), «Доказательство гипотезы о конечных модульных решетках», Теоремы Дилворта: Избранные статьи Роберта П. Дилворта , Современные математики, Бостон: Биркхойзер, стр. 219–224, номер документа : 10.1007/978-1-4899- 3558-8_21 , ISBN 978-1-4899-3560-1
^ Французский термин , обозначающий модульную пару, — «para modulaire» . Пара ( a, b ) во французском языке называется модульной парой , если оба ( a, b ) и ( b, a ) являются модулярными парами.
^ Модульный элемент по-разному определялся разными авторами и обозначал правомодулярный ( Stern (1999 , стр. 74)), левый модульный ( Orlik & Terao (1992 , Определение 2.25)), как левый, так и правый модульный (или двойной правомодулярный). ( Саган (1999) , Шмидт (1994 , стр. 43)), или удовлетворяющие условию модульного ранга ( Стэнли (2007 , определение 4.12)). Эти понятия эквивалентны в полумодулярной решетке, но не в общем случае.
^ Некоторые авторы, например Фофанова (2001), называют такие решетки полумодулярными решетками . Поскольку каждая M-симметричная решетка полумодулярна и обратное справедливо для решеток конечной длины, это может привести только к путанице для бесконечных решеток.
^ Jump up to: ^а ^б ^с ^д ^и ^ж ^г Дедекинд, Рихард (1897), «О разложении чисел по их наибольшим общим делителям» (PDF) , Festschrift der Herzogl. Технический университет Кароло-Вильгельмина по случаю 69-й встречи немецких естествоиспытателей и врачей в Брауншвейге , Фридрих Видег и сын
^ Дедекинд, Ричард (1900), «О двойственной группе, порожденной тремя модулями» , Mathematical Annals , 53 (3): 371–403, doi : 10.1007/BF01448979 , S2CID 122529830

Ссылки

Корри, Лео (27 ноября 2003 г.), Современная алгебра и возникновение математических структур (2-е изд.), стр. 121–129, ISBN. 978-3-7643-7002-2
Фофанова, Т. С. (2001) [1994], «Полумодульная решетка» , Энциклопедия Математики , EMS Press
Маэда, Сюитиро (1965), «О симметрии модулярного соотношения в атомных решетках» , Научный журнал Университета Хиросимы , 29 : 165–170.
Орлик, Петр ; Терао, Хироаки (1992), Расположение гиперплоскостей , Основы математических наук, том. 300, Шпрингер-Верлаг, номер номера : 10.1007/978-3-662-02772-1.
Рота, Джан-Карло (1997), «Множество жизней теории решетки» (PDF) , Уведомления Американского математического общества , 44 (11): 1440–1445, ISSN 0002-9920
Скорняков, Л. А. (2001) [1994], «Модульная решетка» , Энциклопедия Математики , EMS Press
Саган, Брюс (1999), «Почему характеристические полиномиальные коэффициенты», Бюллетень Американского математического общества , 36 (2): 113–133, arXiv : math/9812136 , doi : 10.1090/S0273-0979-99-00775-2
Шмидт, Роланд (1994), Решетки подгрупп групп , Изложения де Грюйтера по математике, том. 14, Уолтер де Грюйтер и компания, номер документа : 10.1515/9783110868647 , ISBN. 3-11-011213-2
Стэнли, Ричард П. (2007), «Введение в компоновку гиперплоскости», Геометрическая комбинаторика , IAS/Park City Mathematics Series, vol. 13, Американское математическое общество, стр. 389–496, ISBN. 978-0-8218-3736-8
Стерн, Манфред (1999), Полумодулярные решетки , Cambridge University Press , ISBN 978-0-521-46105-4

Внешние ссылки

«Модульная решетка» . ПланетаМатематика .
Последовательность OEIS A006981 (Количество немаркированных модульных решеток с n элементами)
Бесплатный генератор модульных решеток Веб-приложение на основе браузера с открытым исходным кодом, которое может генерировать и визуализировать некоторые бесплатные модульные решетки.

[1] «Почему модульные решетки важны?» . Математический обмен стеками . Проверено 17 сентября 2018 г.

[2] Для любой решетки верно следующее: $а \lor (Икс \land б) \leq (а \lor Икс) \land (а \lor б)$ . Кроме того, всякий раз, когда $a \leq b$ , тогда $a \lor b = b$ .

[:0-3] Блит, Т.С. (2005). «Модульные решетки» . Решетки и упорядоченные алгебраические структуры . Университеттекст. Лондон: Спрингер. Теорема 4.4. дои : 10.1007/1-84628-127-X_4 . ISBN 978-1-85233-905-0 .

[4] Блит, Т.С. (2005). «Модульные решетки» . Решетки и упорядоченные алгебраические структуры . Университеттекст. Лондон: Спрингер. п. 65. дои : 10.1007/1-84628-127-X_4 . ISBN 978-1-85233-905-0 .

[5] В дистрибутивной решетке справедливо следующее: $(a\wedge b)\vee (x\wedge b)=((a\wedge b)\vee x)\wedge ((a\wedge b)\vee b)$ . Кроме того, закон поглощения $(a\wedge b)\vee b=b$ , справедливо для любой решетки. Подстановка этого второго соединения в правую часть первого уравнения дает модульную идентичность.

[6] Дилворт, Р.П. (1954), «Доказательство гипотезы о конечных модулярных решетках», Annals of Mathematics , Second Series, 60 (2): 359–364, doi : 10.2307/1969639 , JSTOR 1969639 , MR 0063348 . Перепечатано в Богарт, Кеннет П.; Фриз, Ральф; Кунг, Джозеф PS, ред. (1990), «Доказательство гипотезы о конечных модульных решетках», Теоремы Дилворта: Избранные статьи Роберта П. Дилворта , Современные математики, Бостон: Биркхойзер, стр. 219–224, номер документа : 10.1007/978-1-4899- 3558-8_21 , ISBN 978-1-4899-3560-1

[7] Французский термин , обозначающий модульную пару, — «para modulaire» . Пара ( a, b ) во французском языке называется модульной парой , если оба ( a, b ) и ( b, a ) являются модулярными парами.

[8] Модульный элемент по-разному определялся разными авторами и обозначал правомодулярный ( Stern (1999 , стр. 74)), левый модульный ( Orlik & Terao (1992 , Определение 2.25)), как левый, так и правый модульный (или двойной правомодулярный). ( Саган (1999) , Шмидт (1994 , стр. 43)), или удовлетворяющие условию модульного ранга ( Стэнли (2007 , определение 4.12)). Эти понятия эквивалентны в полумодулярной решетке, но не в общем случае.

[9] Некоторые авторы, например Фофанова (2001), называют такие решетки полумодулярными решетками . Поскольку каждая M-симметричная решетка полумодулярна и обратное справедливо для решеток конечной длины, это может привести только к путанице для бесконечных решеток.

[Dedekind.1897-10] Jump up to: ^а ^б ^с ^д ^и ^ж ^г Дедекинд, Рихард (1897), «О разложении чисел по их наибольшим общим делителям» (PDF) , Festschrift der Herzogl. Технический университет Кароло-Вильгельмина по случаю 69-й встречи немецких естествоиспытателей и врачей в Брауншвейге , Фридрих Видег и сын

[11] Дедекинд, Ричард (1900), «О двойственной группе, порожденной тремя модулями» , Mathematical Annals , 53 (3): 371–403, doi : 10.1007/BF01448979 , S2CID 122529830

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]