Свободная булева алгебра

В математике свободная булева алгебра — это булева алгебра с выделенным набором элементов, называемых генераторами , такими, что:

Каждый элемент булевой алгебры можно выразить как конечную комбинацию образующих с использованием булевых операций и
Генераторы настолько независимы , насколько это возможно, в том смысле, что между ними нет отношений (опять же в терминах конечных выражений с использованием булевых операций), которые не соблюдаются в каждой булевой алгебре, независимо от того, какие элементы выбраны.

Простой пример

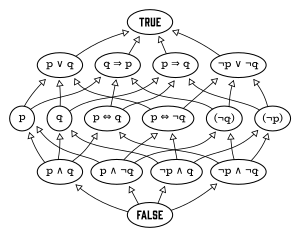
Диаграмма Хассе свободной булевой алгебры с двумя образующими p и q. Возьмите p (левый кружок) как «Джон высокий», а q (правый кружок) как «Мэри богатая». Атомы — это четыре элемента в строке чуть выше ЛОЖЬ. — The Hasse diagram of the free Boolean algebra on two generators, p and q. Take *p (left circle)* to be "John is tall" and *q (right circle)*to be "Mary is rich". The atoms are the four elements in the row just above FALSE.

Генераторы независимые свободной булевой алгебры могут представлять предложения . Рассмотрим, например, предложения «Джон высокий» и «Мэри богатая». Они порождают булеву алгебру с четырьмя атомами , а именно:

Джон высокий, а Мэри богатая;
Джон высок, а Мэри небогата;
Джон невысокий, а Мэри богатая;
Джон невысокий, а Мэри небогатая.

Другие элементы булевой алгебры представляют собой логические дизъюнкции атомов, например: «Джон высокий, а Мэри небогатая, или Джон невысокий, а Мэри богатая». Кроме того, есть еще один элемент, ЛОЖЬ, который можно рассматривать как пустую дизъюнкцию; то есть дизъюнкция атомов отсутствует.

В этом примере получается булева алгебра с 16 элементами; вообще говоря, для конечного n свободная булева алгебра с n генераторами имеет 2 ^н атомы и, следовательно, $2^{2^{n}}$ элементы.

Если бесконечно много генераторов нет , то преобладает аналогичная ситуация, за исключением того, что теперь атомов . Каждый элемент булевой алгебры представляет собой комбинацию конечного числа порождающих предложений, причем два таких элемента считаются идентичными, если они логически эквивалентны .

Другой способ понять, почему свободная булева алгебра на наборе из n элементов имеет $2^{2^{n}}$ elements, следует отметить, что каждый элемент представляет собой функцию от n бит до одного. Есть $2^{n}$ возможные входные данные для такой функции, и функция выберет 0 или 1 для вывода для каждого входа, поэтому есть $2^{2^{n}}$ возможные функции.

Теоретико-категорное определение

На языке теории категорий свободные булевы алгебры могут быть определены просто в терминах присоединения между категорией множеств и функций Set и категорией булевых алгебр и гомоморфизмов булевых алгебр BA . Фактически, этот подход обобщается на любую алгебраическую структуру, определяемую в рамках универсальной алгебры .

Выше мы говорили, что свободная булева алгебра — это булева алгебра с набором образующих, которые ведут себя определенным образом; в качестве альтернативы можно начать с набора и спросить, какую алгебру он порождает. Каждое множество X порождает свободную булеву алгебру FX, определенную как алгебру такую, что для каждой алгебры B и функции f : X → B существует единственный гомоморфизм булевой алгебры f ′ : FX → B , который расширяет f . Схематически ,

где i _X — включение, а пунктирная стрелка означает единственность. Идея состоит в том, что как только кто-то выбирает, куда отправить элементы X , законы гомоморфизмов булевой алгебры определяют, куда отправлять все остальное в свободной алгебре FX . Если бы FX содержал элементы, невыразимые как комбинации элементов X , то f ′ не было бы уникальным, а если бы элементы X не были достаточно независимыми, то f ′ не было бы четко определено! Легко показать, что FX единственен (с точностью до изоморфизма), поэтому это определение имеет смысл. Также легко показать, что свободная булева алгебра с порождающим набором X, как она определена первоначально, изоморфна FX , поэтому эти два определения согласуются.

Одним из недостатков приведенного выше определения является то, что диаграмма не отражает того, что f ′ является гомоморфизмом; поскольку это диаграмма в Set, каждая стрелка обозначает простую функцию. Мы можем исправить это, разделив его на две диаграммы: одну в BA и одну в Set . Чтобы связать эти два понятия, мы вводим функтор U : BA → Set , который « забывает » алгебраическую структуру, отображая алгебры и гомоморфизмы в их основные множества и функции.

Если мы интерпретируем верхнюю стрелку как диаграмму в BA диаграмму в Set , то эта диаграмма правильно выражает, что каждая функция f : X → UB продолжается до уникального гомоморфизма булевой алгебры f ′: FX → B. , а нижний треугольник как Функтор U можно рассматривать как устройство, позволяющее вернуть гомоморфизм f ′ обратно в Set, чтобы его можно было связать с f .

Замечательным аспектом этого является то, что последняя диаграмма является одним из различных (эквивалентных) определений того, когда два функтора сопряжены . Наша F легко расширяется до функтора Set → BA , и наше определение X, свободную булеву алгебру FX, состоит в точности в том, что U имеет левое сопряженное F. порождающего

Топологическая реализация

Свободная булева алгебра с κ образующими , где κ – конечное или бесконечное кардинальное число , может быть реализована как совокупность всех открыто-открытых подмножеств {0,1}. ^Мистер, учитывая топологию продукта , предполагая, что {0,1} имеет дискретную топологию . Для каждого α<κ α -й генератор представляет собой набор всех элементов {0,1} ^Мистер координата которой α- я равна 1. В частности, свободная булева алгебра с $\aleph _{0}$ Генераторы — это совокупность всех открыто-замкнутых подмножеств канторова пространства , иногда называемая алгеброй Кантора . Эта коллекция счетна . Фактически, хотя свободная булева алгебра с n образующими, n конечна, имеет мощность $2^{2^{n}}$ , свободная булева алгебра с $\aleph _{0}$ генераторы, как и в любой свободной алгебре с $\aleph _{0}$ генераторов и счетного числа финитных операций, имеет мощность $\aleph _{0}$ .

Дополнительную информацию об этом топологическом подходе к свободной булевой алгебре см. в теореме Стоуна о представлении булевых алгебр .

См. также

Ссылки

Стив Аводи (2006) Теория категорий (Oxford Logic Guides 49). Издательство Оксфордского университета.
Пол Халмос и Стивен Гивант (1998) Логика как алгебра . Математическая ассоциация Америки .
Сондерс Мак Лейн (1998) Категории для работающего математика . 2-е изд. (Выпускные тексты по математике 5). Спрингер-Верлаг.
Сондерс Мак Лейн (1999) Алгебра , 3d. ред. Американское математическое общество . ISBN 0-8218-1646-2 .
Роберт Р. Столл, 1963. Теория множеств и логика , гл. 6.7. Дуврское переиздание 1979 года.