Пилообразная волна

Пилообразная волна
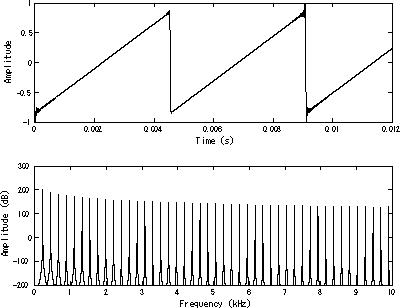с ограниченной полосой пропускания Пилообразная волна изображено во временной области (вверху) и частотной области (внизу). Основная частота составляет 220 Гц (A 3 ).
Общая информация
Общее определение	$x(t)=2\left(t-\left\lfloor t+{\tfrac {1}{2}}\right\rfloor \right),t-{\tfrac {1}{2}}\notin \mathbb {Z}$
Области применения	Электроника, синтезаторы
Домен, кодомен и изображение
Домен	$\mathbb {R} \setminus \left\{n-{\tfrac {1}{2}}\right\},n\in \mathbb {Z}$
Кодомен	$\left(-1,1\right)$
Основные функции
Паритет	Странный
Период	1
Особенности
Корень	$\mathbb {Z}$
ряд Фурье	$x(t)=-{\frac {2}{\pi }}\sum _{k=1}^{\infty }{\frac {{\left(-1\right)}^{k}}{k}}\sin \left(2\pi kt\right)$

Пилообразная волна (или пилообразная волна ) — это своего рода несинусоидальный сигнал . Назван так из-за сходства с зубьями пилы с прямыми зубьями и нулевым передним углом . Одиночный пилообразный сигнал или пилообразный сигнал с периодическим запуском называется пилообразным сигналом .

Условно говоря, пилообразная волна поднимается вверх, а затем резко падает. При обратной (или обратной) пилообразной волне волна сначала снижается, а затем резко возрастает. Ее также можно рассматривать как крайний случай асимметричной треугольной волны .

Эквивалентные кусочно-линейные функции $$x(t)=t-\lfloor t\rfloor$$ $$x(t)=t{\bmod {1}}$$ на основе функции пола от времени t является примером пилообразной волны с периодом 1.

Более общая форма в диапазоне от -1 до 1 и с периодом p : $$2\left({\frac {t}{p}}-\left\lfloor {\frac {1}{2}}+{\frac {t}{p}}\right\rfloor \right)$$

Эта пилообразная функция имеет ту же фазу , что и синусоидальная функция.

В то время как прямоугольная волна состоит только из нечетных гармоник, звук пилообразной волны резкий и чистый, а ее спектр содержит как четные, так и нечетные гармоники основной частоты . Поскольку он содержит все целочисленные гармоники, это одна из лучших форм волны для субтрактивного синтеза музыкальных звуков, особенно смычковых струнных инструментов, таких как скрипки и виолончели, поскольку скользящее поведение смычка приводит в движение струны с пилообразным движением. движение.

Пилообразную форму можно построить с помощью аддитивного синтеза . Для периода p и амплитуды a следующие бесконечные ряды Фурье сходятся к пилообразной и обратной (обратной) пилообразной волне:

$$f={\frac {1}{p}}$$ $$x_{\text{sawtooth}}(t)=a\left({\frac {1}{2}}-{\frac {1}{\pi }}\sum _{k=1}^{\infty }{(-1)}^{k}{\frac {\sin(2\pi kft)}{k}}\right)$$ $$x_{\text{reverse sawtooth}}(t)={\frac {2a}{\pi }}\sum _{k=1}^{\infty }{(-1)}^{k}{\frac {\sin(2\pi kft)}{k}}$$

При цифровом синтезе эти ряды суммируются только по k так, что высшая гармоника N _max меньше частоты Найквиста (половины частоты дискретизации ). Это суммирование обычно можно более эффективно вычислить с помощью быстрого преобразования Фурье . Если форма волны создается в цифровом виде непосредственно во временной области с использованием формы без ограничения полосы пропускания , например y = x −floor искажения ( x ), дискретизируются бесконечные гармоники, и результирующий тон содержит из-за наложения спектров .

Анимация аддитивного синтеза пилообразной волны с возрастающим числом гармоник

Аудиодемонстрация пилообразного звука, воспроизводимого на частотах 440 Гц (A ₄ ), 880 Гц (A ₅ ) и 1760 Гц (A ₆ ), доступна ниже. Представлены как тональные сигналы с ограниченной полосой пропускания (без псевдонимов), так и с псевдонимами.

Приложения

• Пилообразные волны известны своим использованием в музыке. Пилообразные и прямоугольные волны являются одними из наиболее распространенных форм сигналов, используемых для создания звуков с помощью субтрактивных аналоговых и виртуальных аналоговых музыкальных синтезаторов.
• Пилообразные волны используются в импульсных источниках питания . В микросхеме регулятора сигнал обратной связи с выхода постоянно сравнивается с высокочастотным пилообразным сигналом для генерации нового ШИМ-сигнала рабочего цикла на выходе компаратора .
• В области информатики, особенно в области автоматизации и робототехники, $\mathrm {sawtooth} (\theta )=2\arctan(\tan({\frac {\theta }{2}}))$ позволяет рассчитывать суммы и разности углов, избегая разрывов на 360° и 0°.
• Пилообразная волна — это форма сигналов вертикального и горизонтального отклонения , используемая для создания растра на ЭЛТ -телевидении или экранах мониторов. Осциллографы также используют пилообразную волну для горизонтального отклонения, хотя обычно они используют электростатическое отклонение.
  • На «рампе» волны магнитное поле, создаваемое отклоняющим ярмом, увлекает электронный луч через поверхность ЭЛТ, создавая линию сканирования .
  • На «обрыве» волны магнитное поле внезапно разрушается, заставляя электронный луч как можно быстрее вернуться в исходное положение.
  • Ток, подаваемый на отклоняющее ярмо, регулируется различными средствами (трансформаторами, конденсаторами, обмотками с центральным отводом) так, чтобы среднее напряжение на обрыве пилообразного элемента находилось на нулевой отметке, а это означает, что отрицательный ток вызовет отклонение в одном направлении. , и положительное отклонение тока в другом; таким образом, установленное в центре отклоняющее ярмо может использовать всю площадь экрана для отображения следа. Частота горизонтальной развертки составляет 15,734 кГц для NTSC , 15,625 кГц для PAL и SECAM .
  • Система вертикального отклонения работает так же, как и горизонтальная, но на гораздо более низкой частоте (59,94 Гц для NTSC , 50 Гц для PAL и SECAM).
  • Наклонная часть волны должна выглядеть как прямая линия. В противном случае это означает, что ток не увеличивается линейно и, следовательно, магнитное поле, создаваемое отклоняющим ярмом, не является линейным. В результате электронный луч будет ускоряться на нелинейных участках. Это приведет к тому, что телевизионное изображение будет «сплющено» в сторону нелинейности. В крайних случаях будет наблюдаться заметное увеличение яркости, поскольку электронный луч проводит больше времени на этой стороне изображения.
  • Первые телевизионные приемники имели элементы управления, позволяющие пользователям регулировать вертикальную или горизонтальную линейность изображения. Таких элементов управления не было в более поздних комплектах, поскольку стабильность электронных компонентов улучшилась.

См. также

Синусоидальная , прямоугольная , треугольная и пилообразная формы сигналов.

• Список периодических функций
• Синусоидальная волна
• Прямоугольная волна
• Треугольная волна
• Пульсовая волна
• Звук
• Волна
• Зигзаг

Внешние ссылки

• Хью Л. Монтгомери ; Роберт С. Воган (2007). Мультипликативная теория чисел I. Классическая теория . Кембриджские трактаты по высшей математике. Том. 97. стр. 536–537. ISBN  978-0-521-84903-6 .