Правило подсчета очков

Не путать с голосованием по очкам .

Визуализация ожидаемого результата при различных прогнозах некоторых общих функций оценки. Пунктирная черная линия: истинное мнение прогнозиста, красная: линейная, оранжевая: сферическая, фиолетовая: квадратичная, зеленая: логарифмическая.

В теории принятия решений правило подсчета очков предоставляет метрики оценки для вероятностных предсказаний или прогнозов . В то время как «обычные» функции потерь (такие как среднеквадратическая ошибка ) присваивают оценку согласия прогнозируемому значению и наблюдаемому значению, правила оценки присваивают такую ​​оценку прогнозируемому распределению вероятностей и наблюдаемому значению. С другой стороны, функция оценки обеспечивает сводную меру для оценки точечных прогнозов, т.е. прогнозирует свойство или функционал $T(F)$, как ожидание или медиана .

Средний логарифмический балл в 10 000 баллов выбран из стандартного нормального распределения (синяя гистограмма), оцененного по различным распределениям (красная линия). Хотя это не обязательно верно для отдельных точек, в среднем правильное правило подсчета очков дает наименьший балл, если прогнозируемое распределение соответствует распределению данных.

Калибровочная кривая позволяет судить, насколько хорошо откалиброваны прогнозы модели, путем сравнения предсказанных квантилей с наблюдаемыми квантилями. Синий — лучшая откалиброванная модель, см. калибровку (статистику) .

Правила подсчета очков направлены на ответ на вопрос: «Насколько хорошо прогнозируемое распределение вероятностей по сравнению с наблюдением?» Важным свойством правил подсчета очков является (строгая) уместность . По сути, доказано, что (строго) правильные правила оценки дают наименьший ожидаемый балл, если прогнозируемое распределение равно базовому распределению целевой переменной. Хотя это может отличаться для отдельных наблюдений, это должно привести к минимизации ожидаемого балла, если прогнозируются «правильные» распределения.

Правила оценки и функции оценки часто используются как «функции затрат» или « функции потерь » в моделях вероятностного прогнозирования. Они оцениваются как эмпирическое среднее значение данной выборки, «балл». Затем можно сравнить оценки различных прогнозов или моделей, чтобы сделать вывод, какая модель лучше. Например, рассмотрим модель, которая предсказывает (на основе входных данных $x$) среднее $\mu \in \mathbb {R}$ и стандартное отклонение $\sigma \in \mathbb {R} _{+}$. Вместе эти переменные определяют гауссово распределение. ${\mathcal {N}}(\mu ,\sigma ^{2})$, по сути предсказывая целевую переменную как распределение вероятностей. Распространенная интерпретация вероятностных моделей заключается в том, что они направлены на количественную оценку собственной неопределенности прогнозов. В этом примере наблюдаемая целевая переменная $y\in \mathbb {R}$ затем проводится сравнение с предсказанным распределением ${\mathcal {N}}(\mu ,\sigma ^{2})$ и присвоил балл ${\mathcal {L}}({\mathcal {N}}(\mu ,\sigma ^{2}),y)\in \mathbb {R}$. При обучении правилу оценки следует «научить» вероятностную модель прогнозировать, когда ее неопределенность низкая, а когда ее неопределенность высока, и это должно привести к калиброванным прогнозам, минимизируя при этом неопределенность прогнозирования.

Хотя приведенный пример касается вероятностного прогнозирования реальной целевой переменной, было разработано множество различных правил оценки с учетом разных целевых переменных. Правила оценки существуют для бинарной и категориальной вероятностной классификации , а также для одномерной и многомерной вероятностной регрессии .

Определения

Рассмотрим образец пространства $\Omega$, и σ-алгебра ${\mathcal {A}}$ подмножеств $\Omega$ и выпуклый класс ${\mathcal {F}}$ вероятностных мер на $(\Omega ,{\mathcal {A}})$. Функция, определенная на $\Omega$ и принимая значения в расширенной действительной линии, ${\overline {\mathbb {R} }}=[-\infty ,\infty ]$, является ${\mathcal {F}}$-квазиинтегрируемая, если она измерима с помощьюуважение к ${\mathcal {A}}$ и квазиинтегрируемо относительно всех $F\in {\mathcal {F}}$.

Вероятностный прогноз

Вероятностный прогноз – это любая вероятностная мера. $F\in {\mathcal {F}}$. Т.е. это распределение потенциальных будущих наблюдений.

Правило подсчета очков

Правило оценки — это любая расширенная функция с действительным знаком. $\mathbf {S} :{\mathcal {F}}\times \Omega \rightarrow \mathbb {R}$ такой, что $\mathbf {S} (F,\cdot )$ является ${\mathcal {F}}$-квазиинтегрируемый для всех $F\in {\mathcal {F}}$. $\mathbf {S} (F,y)$ представляет собой убыток или штраф, когда прогноз $F\in {\mathcal {F}}$ выдается и наблюдение $y\in \Omega$ материализуется .

Точечный прогноз

Точечный прогноз представляет собой функционал, т. е. потенциально многозначное отображение. $F\rightarrow T(F)\subseteq \Omega$.

Функция подсчета очков

Функция оценки — это любая функция с действительным знаком. $S:\Omega \times \Omega \rightarrow \mathbb {R}$ где $S(x,y)$ представляет собой потерю или штраф, когда прогнозируемая точка $x\in \Omega$ выдается и наблюдение $y\in \Omega$ материализуется.

Ориентация

Правила подсчета очков $\mathbf {S} (F,y)$ и функции оценки $S(x,y)$ отрицательно (положительно) ориентированы, если меньшие (большие) значения означают лучше. Здесь мы придерживаемся негативной направленности, отсюда и ассоциация с «потерей».

результат

Пишем для ожидаемой оценки прогноза $F$ под $Q\in {\mathcal {F}}$ как ожидаемый балл прогнозируемого распределения $F\in {\mathcal {F}}$, при выборке наблюдений из распределения $Q$.

$\mathbb {E} _{Y\sim Q}[S(F,Y)]=\int \mathbf {S} (F,\omega )\mathrm {d} Q(\omega )$

Примерный средний балл

Многие модели вероятностного прогнозирования обучаются с использованием выборочного среднего балла, в котором набор прогнозируемых распределений $F_{1},\ldots ,F_{n}\in {\mathcal {F}}$ оценивается по набору наблюдений $y_{1},\ldots ,y_{n}\in \Omega$.

${\mathcal {L}}={\frac {1}{n}}\sum _{i=1}^{n}S(F_{i},y_{i})$

Уместность и последовательность

Строго правильные правила подсчета очков и строго последовательные функции подсчета очков способствуют составлению честных прогнозов за счет максимизации ожидаемого вознаграждения: $-\mathbf {S} (F,y)$ если $y$ осознает (например $y=rain$), то наивысшая ожидаемая награда (самый низкий балл) будет получена путем сообщения об истинном распределении вероятностей.

Правильные правила подсчета очков

Правило подсчета очков $\mathbf {S}$ является правильным относительно ${\mathcal {F}}$ если (предполагая отрицательную ориентацию) его ожидаемая оценка минимизируется, когда прогнозируемое распределение соответствует распределению наблюдения.

$\mathbb {E} _{Y\sim Q}[S(Q,Y)]\leq \mathbb {E} _{Y\sim Q}[S(F,Y)]$ для всех $F,Q\in {\mathcal {F}}$.

Строго правильно, если приведенное выше уравнение выполняется с равенством тогда и только тогда, когда $F=Q$.

Последовательные функции оценки

Функция подсчета очков $S$ согласован функционалу по $T$ относительно класса ${\mathcal {F}}$ если

$\mathbb {E} _{Y\sim F}[S(t,Y)]\leq \mathbb {E} _{Y\sim F}[S(x,Y)]$ для всех $F\in {\mathcal {F}}$, все $t\in T(F)$ и все $x\in \Omega$.

Оно строго непротиворечиво, если оно непротиворечиво, а равенство в приведенном выше уравнении означает, что $x\in T(F)$.

Пример применения правил подсчета очков

Логарифмическое правило

Примером вероятностного прогнозирования является метеорология, где синоптик может указать вероятность дождя на следующий день. Можно отметить, сколько раз за длительный период указывалась вероятность 25%, и сравнить это с фактической долей случаев, когда выпадал дождь. Если реальный процент существенно отличался от заявленной вероятности, мы говорим, что прогнозист плохо откалиброван . Плохо калиброванный прогнозист может быть поощрен системой бонусов . Система бонусов, разработанная на основе правильных правил подсчета очков, будет стимулировать прогнозиста сообщать о вероятностях, равных его личным убеждениям .

В дополнение к простому случаю двоичного решения , такого как присвоение вероятностей «дождь» или «нет дождя», правила оценки могут использоваться для нескольких классов, таких как «дождь», «снег», «ясно» или «ясно». непрерывные реакции, такие как количество дождя в день.

На изображении справа показан пример правила логарифмической оценки в зависимости от вероятности события, которое действительно произошло. Одним из способов использования этого правила может быть определение стоимости на основе вероятности, которую назначает прогнозист или алгоритм, а затем проверка того, какое событие действительно происходит.

Примеры правильных правил подсчета очков

Существует бесконечное количество правил подсчета очков, включая целые параметризованные семейства строго правильных правил подсчета очков. Показанные ниже — это просто популярные примеры.

Категориальные переменные

Для категориальной переменной ответа с $m$ взаимоисключающие события, $Y\in \Omega =\{1,\ldots ,m\}$, вероятностный прогнозист или алгоритм вернет вектор вероятности $\mathbf {r}$ с вероятностью для каждого из $m$ результаты.

Логарифмический счет

См. также: Девиантность (статистика)

Ожидаемое значение логарифмического правила, когда ожидается, что событие 1 произойдет с вероятностью 0,8, синяя линия описывается функцией $0.8\log(x)+(1-0.8)\log(1-x)$

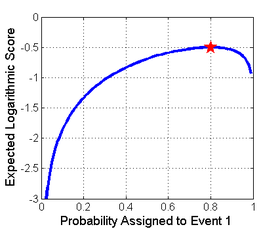
Логарифмическое правило подсчета очков является локальным строго правильным правилом подсчета очков. Это также является отрицательным моментом неожиданности , которая обычно используется в качестве критерия оценки в байесовском выводе ; цель состоит в том, чтобы свести к минимуму ожидаемое удивление. Это правило подсчета очков имеет прочную основу в теории информации .

$L(\mathbf {r} ,i)=\ln(r_{i})$

Здесь оценка рассчитывается как логарифм оценки вероятности фактического результата. То есть предсказание в 80 %, которое правильно подтвердилось, получит оценку ln(0,8) = −0,22 . Этот же прогноз также присваивает вероятность 20% противоположному случаю, и поэтому, если прогноз окажется ложным, он получит оценку, основанную на 20%: ln(0,2) = −1,6 . Цель прогнозиста — максимизировать оценку и сделать ее как можно большей, а −0,22 действительно больше, чем −1,6.

Если рассматривать истинность или ложность прогноза как переменную x со значением 1 или 0 соответственно, а выраженную вероятность как p , то можно записать логарифмическое правило оценки как x ln( p ) + (1 − x ) ln( 1 - п ) . Обратите внимание, что можно использовать любую логарифмическую базу, поскольку строго правильные правила подсчета очков остаются строго правильными при линейном преобразовании. То есть:

$L(\mathbf {r} ,i)=\log _{b}(r_{i})$

строго подходит для всех $b>1$.

Оценка Брайера/квадратическая оценка

Правило квадратичного подсчета очков является строго правильным правилом подсчета очков.

$Q(\mathbf {r} ,i)=2r_{i}-\mathbf {r} \cdot \mathbf {r} =2r_{i}-\sum _{j=1}^{C}r_{j}^{2}$

где $r_{i}$ - вероятность, присвоенная правильному ответу и $C$ это количество классов.

Оценка Брайера , первоначально предложенная Гленном В. Брайером в 1950 году, может быть получено с помощью аффинного преобразования из правила квадратичного подсчета очков.

$B(\mathbf {r} ,i)=\sum _{j=1}^{C}(y_{j}-r_{j})^{2}$

Где $y_{j}=1$ когда $j$это событие является правильным и $y_{j}=0$ в противном случае и $C$ это количество классов.

Важная разница между этими двумя правилами заключается в том, что прогнозист должен стремиться максимизировать квадратичный балл. $Q$ но минимизировать оценку Брайера $B$. Это связано с отрицательным знаком линейного преобразования между ними.

Правило подсчета очков Хюварина

Функция оценки Хюваринен (плотности p) определяется выражением

$s(p)=2\Delta _{y}\log p(y)+\|\nabla _{y}\log p(y)\|_{2}^{2}$

Где $\Delta$ обозначает гессианский след и $\nabla$ обозначает градиент . Это правило оценки можно использовать для вычислительного упрощения вывода параметров и сравнения байесовской модели с произвольно неопределенными априорными данными. Он также использовался для введения новых теоретико-информационных величин, выходящих за рамки существующей теории информации .

Сферическая оценка

Сферическое правило подсчета очков также является строго правильным правилом подсчета очков.

$S(\mathbf {r} ,i)={\frac {r_{i}}{\lVert \mathbf {r} \rVert }}={\frac {r_{i}}{\sqrt {r_{1}^{2}+\cdots +r_{C}^{2}}}}$

Ранжированная оценка вероятности

Ранжированная оценка вероятности (RPS) – это строго правильное правило подсчета очков, которое можно выразить следующим образом:

$RPS(\mathbf {r} ,i)=\sum _{k=1}^{C-1}\left(\sum _{j=1}^{k}r_{j}-y_{j}\right)^{2}$

Где $y_{j}=1$ когда $j$это событие является правильным и $y_{j}=0$ в противном случае, и $C$ это количество классов. В отличие от других правил оценки, ранжированная оценка вероятности учитывает расстояние между классами, т. е. классы 1 и 2 считаются более близкими, чем классы 1 и 3. Эта оценка присваивает более высокие оценки вероятностным прогнозам, при этом высокие вероятности присваиваются классам, близким к правильному классу. Например, при рассмотрении вероятностных прогнозов $\mathbf {r} _{1}=(0.5,0.5,0)$ и $\mathbf {r} _{2}=(0.5,0,0.5)$, мы находим это $RPS(\mathbf {r} _{1},1)=0.25$, пока $RPS(\mathbf {r} _{2},1)=0.5$, несмотря на то, что оба вероятностных прогноза приписывают одинаковую вероятность правильному классу.

категориальных строго правильных правил

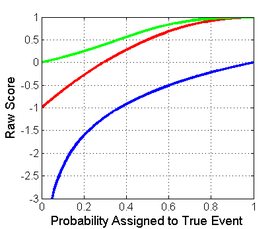
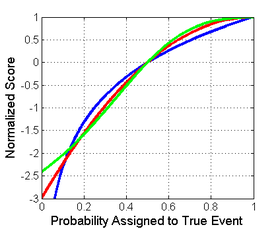
Ниже слева показано графическое сравнение логарифмических, квадратичных и сферических правил оценки для задачи бинарной классификации. Ось X указывает заявленную вероятность события, которое действительно произошло.

Важно отметить, что каждая из оценок имеет разную величину и местоположение. Однако различия в величинах не имеют значения, поскольку оценки остаются правильными при аффинном преобразовании. Поэтому для сравнения разных оценок необходимо привести их к общей шкале. Разумный выбор нормализации показан на рисунке справа, где все оценки пересекают точки (0,5,0) и (1,1). Это гарантирует, что они дают 0 для равномерного распределения (две вероятности по 0,5 каждая), что означает отсутствие затрат или вознаграждения за сообщение о том, что часто является базовым распределением. Все приведенные ниже нормализованные оценки также дают 1, если истинному классу присвоена вероятность 1.

Оценка двоичной классификации истинного класса, показывающая логарифмическую (синий), сферическую (зеленый) и квадратичную (красный)

Нормализованная оценка бинарной классификации для истинного класса, показывающая логарифмический (синий), сферический (зеленый) и квадратичный (красный)

Одномерные непрерывные переменные

Перечисленные ниже правила оценки направлены на оценку вероятностных прогнозов, когда прогнозируемые распределения представляют собой одномерные непрерывные распределения вероятностей , т. е. прогнозируемые распределения определены для одномерной целевой переменной. $X\in \mathbb {R}$ и имеют функцию плотности вероятности $f:\mathbb {R} \to \mathbb {R} _{+}$.

оценка для

Логарифмический балл — это локальное строго правильное правило подсчета очков. Это определяется как

$L(D,y)=-\ln(f_{D}(y))$

где $f_{D}$ обозначает функцию плотности вероятности предсказанного распределения $D$. Это местное строгое правило подсчета очков. Логарифмический балл для непрерывных переменных тесно связан с оценкой максимального правдоподобия . Однако во многих приложениях непрерывная ранжированная оценка вероятности часто предпочтительнее логарифмической оценки, поскольку на логарифмическую оценку могут сильно влиять небольшие отклонения в плотности хвостов прогнозируемых распределений.

Непрерывная ранжированная оценка вероятности

Иллюстрация непрерывного ранжированного показателя вероятности (CRPS). Учитывая выборку y и предсказанное кумулятивное распределение F, CRPS определяется путем вычисления разницы между кривыми в каждой точке x опоры, возведения ее в квадрат и интегрирования по всей опоре.

Непрерывная ранжированная оценка вероятности (CRPS) — это строго правильное правило подсчета очков, широко используемое в метеорологии. Это определяется как

$CRPS(D,y)=\int _{\mathbb {R} }(F_{D}(x)-H(x\geq y))^{2}dx$

где $F_{D}$ - кумулятивная функция распределения прогнозируемого распределения $D$, $H$ – ступенчатая функция Хевисайда и $y\in \mathbb {R}$ это наблюдение. Для распределений с конечным первым моментом непрерывную ранжированную оценку вероятности можно записать как:

$CRPS(D,y)=\mathbb {E} _{X\sim D}[|X-y|]-{\frac {1}{2}}\mathbb {E} _{X,X'\sim D}[|X-X'|]$

где $X$ и $X'$ являются независимыми случайными величинами, выбранными из распределения $D$. Кроме того, когда кумулятивная функция вероятности $F$ является непрерывным, непрерывную ранжированную оценку вероятности также можно записать как

$CRPS(D,y)=\mathbb {E} _{X\sim D}[|X-y|]+\mathbb {E} _{X\sim D}[X]-2\mathbb {E} _{X\sim D}[X\cdot F_{D}(X)]$

Непрерывную ранжированную оценку вероятности можно рассматривать как непрерывное расширение ранжированной оценки вероятности, а также как квантильную регрессию . Непрерывная ранжированная оценка вероятности по эмпирическому распределению ${\hat {D}}_{q}$ упорядоченных заданных точек $q_{1}\leq \ldots \leq q_{n}$ (т.е. каждая точка имеет $1/n$ вероятность возникновения), равна удвоенной средней потере квантилей , примененной к точкам с равномерно распределенными квантилями. $(\tau _{1},\ldots ,\tau _{n})=(1/(2n),\ldots ,(2n-1)/(2n))$:

$CRPS\left({\hat {D}}_{q},y\right)={\frac {2}{n}}\sum _{i=1}^{n}\tau _{i}(y-q_{i})_{+}+(1-\tau _{i})(q_{i}-y)_{+}$

Для многих популярных семейств распределений были получены выражения в замкнутой форме для непрерывной ранжированной оценки вероятности. Непрерывная ранжированная оценка вероятности использовалась в качестве функции потерь для искусственных нейронных сетей , в которых прогнозы погоды подвергаются постобработке до распределения вероятностей по Гауссу .

Многомерные непрерывные переменные

Перечисленные ниже правила оценки направлены на оценку вероятностных прогнозов, когда прогнозируемые распределения представляют собой одномерные непрерывные распределения вероятностей , т. е. прогнозируемые распределения определены для многомерной целевой переменной. $X\in \mathbb {R} ^{n}$ и имеют функцию плотности вероятности $f:\mathbb {R} ^{n}\to \mathbb {R} _{+}$.

Многомерный логарифмический балл

Многомерный логарифмический балл аналогичен одномерному логарифмическому баллу:

$L(D,y)=-\ln(f_{D}(y))$

где $f_{D}$ обозначает функцию плотности вероятности предсказанного многомерного распределения $P$. Это местное строгое правило подсчета очков.

Энергетический показатель

Оценка энергии представляет собой многомерное расширение непрерывной ранжированной оценки вероятности:

$ES_{\beta }(D,Y)=\mathbb {E} _{X\sim D}[\lVert X-Y\rVert _{2}^{\beta }]-{\frac {1}{2}}\mathbb {E} _{X,X'\sim D}[\lVert X-X'\rVert _{2}^{\beta }]$

Здесь, $\beta \in (0,2)$, $\lVert \rVert _{2}$ обозначает $n$-мерное евклидово расстояние и $X,X'$ представляют собой независимо выбранные случайные величины из распределения вероятностей. $D$. Оценка энергии строго соответствует распределениям $D$ для чего $\mathbb {E} _{X\sim D}[\lVert X\rVert _{2}]$ конечно. Было высказано предположение, что показатель энергии несколько неэффективен при оценке структуры взаимозависимых зависимостей прогнозируемого многомерного распределения. Энергетический показатель равен удвоенному энергетическому расстоянию между предсказанным распределением и эмпирическим распределением наблюдения.

Оценка вариограммы

Оценка порядка вариограммы $p$ дается:

$VS_{p}(D,Y)=\sum _{i,j=1}^{n}w_{ij}(|Y_{i}-Y_{j}|^{p}-\mathbb {E} _{X\sim D}[|X_{i}-X_{j}|^{p}])^{2}$

Здесь, $w_{ij}$ являются весами, часто равными 1, и $p>0$ может быть выбран произвольно, но $p=0.5,1$ или $2$ часто используются. $X_{i}$ здесь для обозначения $i$'-я маргинальная случайная величина $X$. Оценка вариограммы подходит для распределений, для которых $(2p)$'-й момент конечен для всех компонентов, но никогда не является строго собственным. Утверждается, что по сравнению с показателем энергии показатель вариограммы является более разборчивым в отношении прогнозируемой корреляционной структуры.

непрерывная ранжированная

Условная непрерывная ранжированная вероятностная оценка (Conditional CRPS или CCRPS) представляет собой семейство (строго) правильных правил оценки. Условный CRPS оценивает прогнозируемое многомерное распределение. $D$ путем оценки CRPS по заданному набору одномерных условных распределений вероятностей прогнозируемого многомерного распределения:

$CCRPS_{\mathcal {T}}(D,Y)=\sum _{i=1}^{k}CRPS(P_{X\sim D}(X_{v_{i}}|X_{j}=Y_{j}{\text{ for }}j\in {\mathcal {C}}_{i}),Y_{v_{i}})$

Здесь, $X_{i}$ это $i$'я предельная переменная $X\sim D$, ${\mathcal {T}}=(v_{i},{\mathcal {C}}_{i})_{i=1}^{k}$ представляет собой набор кортежей, определяющий условную спецификацию (с $v_{i}\in \{1,\ldots ,n\}$ и ${\mathcal {C}}_{i}\subseteq \{1,\ldots ,n\}\setminus \{v_{i}\}$), и $P_{X\sim D}(X_{v_{i}}|X_{j}=Y_{j}{\text{ for }}j\in {\mathcal {C}}_{i})$ обозначает условное распределение вероятностей для $X_{v_{i}}$ учитывая, что все переменные $X_{j}$ для $j\in {\mathcal {C}}_{i}$ равны соответствующим наблюдениям. В случае, если $P_{X\sim D}(X_{v_{i}}|X_{j}=Y_{j}{\text{ for }}j\in {\mathcal {C}}_{i})$ не определено (т. е. его условное событие имеет нулевую вероятность), баллы CRPS по этому распределению определяются как бесконечные. Условный CRPS строго подходит для распределений с конечным первым моментом, если цепное правило включено в условную спецификацию, что означает, что существует перестановка $\phi _{1},\ldots ,\phi _{n}$ из $1,\ldots ,n$ такой, что для всех $1\leq i\leq n$: $(\phi _{i},\{\phi _{1},\ldots ,\phi _{i-1}\})\in {\mathcal {T}}$.

Интерпретация правил правильного подсчета очков

Все правильные правила подсчета очков равны взвешенным суммам (целым с неотрицательным весовым функционалом) потерь в наборе простых двухальтернативных задач принятия решений, которые используют вероятностное предсказание, причем каждая такая задача принятия решения имеет определенную комбинацию связанных параметров стоимости. за ложноположительные и ложноотрицательные решения. правильное правило Строго оценки соответствует наличию ненулевого веса для всех возможных порогов принятия решений. Любое данное правильное правило подсчета очков равно ожидаемым потерям относительно конкретного распределения вероятностей по пороговым значениям принятия решения; таким образом, выбор правила оценки соответствует предположению о распределении вероятностей задач принятия решений, для которых в конечном итоге будут использоваться прогнозируемые вероятности, например, правило оценки квадратичных потерь (или правила Брайера), соответствующее равномерной вероятности того, что порог принятия решения равен где-то между нулем и единицей. Показатель точности классификации (процент правильно классифицированных), однопороговое правило оценки, которое равно нулю или единице в зависимости от того, находится ли прогнозируемая вероятность в соответствующей стороне от 0,5, является правильным правилом оценки, но не строго правильным правилом оценки, поскольку оно оптимизировано (в ожидании) не только путем предсказания истинной вероятности, но и путем предсказания любая вероятность со стороны 0,5, что и истинная вероятность.

Характеристики

Аффинное преобразование

Строго правильное правило оценки, будь то бинарное или мультиклассовое, после аффинного преобразования остается строго правильным правилом оценки. То есть, если $S(\mathbf {r} ,i)$ это строго правильное правило подсчета очков, тогда $a+bS(\mathbf {r} ,i)$ с $b\neq 0$ также является строго правильным правилом подсчета очков, хотя если $b<0$ затем смысл оптимизации правила оценки переключается между максимизацией и минимизацией.

Местонахождение

Правильное правило оценки называется локальным , если его оценка вероятности конкретного события зависит только от вероятности этого события. Это утверждение расплывчато в большинстве описаний, но в большинстве случаев мы можем думать об этом как о том, что оптимальное решение проблемы оценки «при конкретном событии» инвариантно ко всем изменениям в распределении наблюдений, которые оставляют вероятность этого события неизменной. Все двоичные оценки являются локальными, поскольку вероятность, присвоенная событию, которое не произошло, определяется таким образом, что степень гибкости для изменения отсутствует.

Аффинные функции логарифмического правила оценки являются единственными строго правильными локальными правилами оценки на конечном множестве, которое не является двоичным.

Разложение

Ожидаемая ценность правильного правила подсчета очков $S$ можно разложить на сумму трех компонентов, называемых неопределенностью , надежностью и разрешением . которые характеризуют различные признаки вероятностных прогнозов:

$E(S)=\mathrm {UNC} +\mathrm {REL} -\mathrm {RES} .$

Если оценка правильная и отрицательно ориентированная (например, оценка Брайера), все три члена являются положительно определенными.Компонент неопределенности равен ожидаемому баллу прогноза, который постоянно предсказывает среднюю частоту событий.Компонент надежности наказывает плохо калиброванные прогнозы, в которых предсказанные вероятности не совпадают с частотой событий.

Уравнения для отдельных компонентов зависят от конкретного правила подсчета очков.Для оценки Брайера они определяются следующим образом:

$\mathrm {UNC} ={\bar {x}}(1-{\bar {x}})$

$\mathrm {REL} =E(p-\pi (p))^{2}$

$\mathrm {RES} =E(\pi (p)-{\bar {x}})^{2}$

где ${\bar {x}}$ — средняя вероятность возникновения бинарного события $x$, и $\pi (p)$ - условная вероятность события, заданная $p$, то есть $\pi (p)=P(x=1\mid p)$

См. также

• Согласованность
• Правило принятия решения

Литература

• Строго правильные правила подсчета очков, прогнозирование и оценка. Тилманн Гнайтинг и Адриан Э. Рафтери, страницы 359-378, https://doi.org/10.1198/016214506000001437 , pdf

Внешние ссылки

• Видео, сравнивающее сферические, квадратичные и логарифмические правила подсчета очков
• Местные правила подсчета очков
• Правила подсчета очков и анализ решений Образование
• Строго правильные правила подсчета очков
• Правила подсчета очков и неопределенность
• Ущерб, причиненный точностью классификации и другими правилами подсчета баллов за неправильную точность классификации
• Выражения в замкнутой форме непрерывного ранжированного показателя вероятности